数据结构——单链表代码总结
1.单链表结点的定义
typedef struct LNode {
int data;//结点的数据域
struct LNode* next;//结点的指针域,指向下一个结点
}LNode,*LinkList;//LinkList为指向结构体LNode的指针类型结点有两个区域,一个数据域一个结点域。结点域next的数据类型是指向结点的指针(struct LNode*)
定义结点的替代名有两个——LNode和*LinkList。这也代表了LinkList是LNode的指针类型。现规定:虽然*LNode==LinkList,但是在声明结点指针时 用*LNode,声明链表时用LinkList。
至于什么时候用new分配空间,主要看的是要用什么功能,比如声明一个结点指针,如果只是起到指向作用,那就不用new。而如果想要一个结点,则需要用new给LNode*类型分配内存空间(p = new LNode)
注:指针声明有两种方法:
写法一: int *p;
写法二: int* p;
两种写法均可正常编译。
写法一:主要是方便一行语句中声明多个变量使用,
如: int *a, *b, c; (a, b是指向int的指针,c是int型变量)
写法二:更加清晰明确指针的类型。
目前大部分用的都是写法二。
2.单链表的初始化(构建空的单链表)
int InitList(LinkList& L)
{
L = new LNode;
//或 L=(LinkList)malloc(sizeof(LNode));
L->next = NULL;
//'.'和'->'效果相同,这里顺序储存结构用'.',链式储存结构用'->'
return 1;
}我们在主函数里声明LinkList L,然后调用InitList来初始化单链表——1.生成新结点作为头结点(以后的操作中都有头结点),用头指针L指向头结点。2.将头结点的指针域置空。
注:在两种建立单链表的方法里,都已经进行了单链表的初始化。由于要对L进行修改,因此使用了引用。
3.建立单链表——头插法:元素插入在链表头部
(1)从一个空表开始,重复读入数据。
(2)生成新结点,将读入的数据存放到新结点的数据域中。
(3)将新结点插入到首元结点的位置。因此最后输入的数据会存放在第一个结点的数据域。
void CreateList_H(LinkList& L, int n)
{
L = new LNode;
L->next = NULL;
//链表的初始化(如果不写的话要提前对链表进行初始化)
LNode* p;//生成一个结点指针p
for (int i = 0; i < n; i++)
{
p = new LNode;//给p赋予空间
cin >> p->data;//输入p数据域的值
p->next = L->next;//p插入在头结点之后
L->next = p;//p指向下一个结点
}
}这里有三个重点:
1.
LNode* p;//生成一个结点指针p
p = new LNode;//给p赋予空间
本身LNode* p的作用是声明一个结点指针。因此如果想让p变成一个结点,则需要给p赋予空间。因此声明一个结点需要这两句代码(而对于结点指针来说,有第一句就够了)。
2.
p->next = L->next;//p插入在头结点之后
L->next = p;//p指向下一个结点这是头插法建立单链表的灵魂代码:每次生成一个结点p输入数据后,让p放在头结点之后,然后把原先首元节点的地址赋给p的地址域。实现每次插入的都是首元结点。
3.
L = new LNode;
L->next = NULL;
//链表的初始化(如果不写的话要提前对链表进行初始化)也就是说,初始链表的代码已经写在了头插法中。
示例:
int main() {
LinkList L;//约定:LinkList用于声明表,LNode用于声明结点
int n;
cout << "请输入链表长度:";
cin >> n;
CreateList_H(L, n);//如果不加初始化代码,需要加上InitList(L)
LNode* p;
p = L->next;
cout << endl << "循环链表的结果是:";
while (p)
{
printf("%d ", p->data);
p = p->next;
}
cout << endl;
return 0;
}首先用头插法建立单链表。然后遍历链表输出。
这里值得注意的就是遍历链表的方法:
LNode* p;
p = L->next;
while (p)
{
printf("%d ", p->data);
p = p->next;
}建立一个结点指针p,让p指向首元结点。然后直到p为空,一直循环下去即可,每次操作结束都让p=p->next;
因为'1'是最后输入的,所以数据域为'8'的结点为首元结点,以此类推。
4.建立单链表——尾插法:元素插在链表尾部
void CreateList_R(LinkList& L, int n)
{
LNode *r, *p;//不能写成 LNode* r,p;
L = new LNode;
L->next = NULL;
r = L;
for (int i = 0; i < n; i++)
{
p = new LNode;
cin >> p->data;
p->next = NULL;
r->next = p;//把p结点放在最后
r = p;//更新尾指针
}
}(1)从一个空表L开始,将新结点逐个插入到链表的尾部,尾指针r指向链表的尾结点。
(2)初始时,r与L均指向头结点。每读入一个数据元素则申请一个新结点。将新结点变成尾结点后,r指向新结点。
这里有两个重点:
(1)关于两个指针的声明:
LNode *r, *p;//不能写成 LNode* r,p;在开头已经介绍过指针的声明方法,应该强调的是:LNode* 并不是一个数据类型,它只是在一个指针声明时用于更好的明确指针类型。因此有多个指针声明的时候,都需要加上*号。
(2)尾指针的使用:
r = L;尾指针的初始化,都是指向头结点。
p->next = NULL;
r->next = p;//把p结点放在最后
r = p;//更新尾指针新生成的p结点,指针域一定要置空(符合单链表尾结点定义),由于尾指针指向的是尾结点,因此p要放在尾结点后面,最后再更新一下尾指针指向的结点。
示例:
int main() {
LinkList L;//约定:LinkList用于声明表,LNode用于声明结点
int n;
cout << "请输入链表长度:";
cin >> n;
CreateList_R(L, n);//如果不加初始化代码,需要加上InitList(L)
LNode* p;
p = L->next;
cout << endl << "遍历链表的结果是:";
while (p)
{
printf("%d ", p->data);
p = p->next;
}
cout << endl;
return 0;
}与头插法基本一模一样的思路。
只不过最后一个输入的数据变成了尾结点,这点与头插法正好反过来。
5.求单链表长度(不计头结点)
int ListLength(LinkList L)
{
LNode* p;
p = L->next;//p初始时指向首元结点
int i = 0;
while (p)
{
i++;
p = p->next;
}
return i;
}设置一个i用来计数,while循环里的代码可以理解为:i先自己加一次(p刚开始指向首元结点),然后p移动到下一个,进行判断。判断后i根据判断结果是否加一。直到p为空。
注:while循环里的两句是可以调换顺序的。如果i++在前面,那就是额外加了一次,相当于把首元结点计入了。如果i++在后面,那么就是p为空的时候多加了一次,变相统计了首元结点。但是初始时i=0是不能变的。
示例:
int main() {
LinkList L;//约定:LinkList用于声明表,LNode用于声明结点
int n;
cout << "请输入链表的长度:";
cin >> n;
CreateList_R(L, n);
int t = ListLength(L);
cout << "计算后链表的长度为:";
cout << t;
return 0;
}6.取值——取单链表中第i个元素的内容
int GetElem(LinkList L, int i, int& e)
{
LNode* p;
int j = 1;
p = L->next;
while (p && j < i)
{
p = p->next;
j++;
}
if (!p || j > i)
{
return 0;
}
e = p->data;
return 1;
}(1)关于j=1的理解:
取值跟统计链表长度不同,j是要一直跟着p走的(也就是说p指向第几个结点,j就是几),由于p初始为首元结点,因此j为1(i!=1的原因是链表长度会统计到最后,一定会额外加一次,要么刚开始额外加,要么最后额外加)。
(2)while循环里条件的理解:
执行循环的条件有两个:p不为空并且j
(3)if里判断条件的理解:
当while循环退出后,正常情况下应该是i==j并且内容不为空,if就是用来防止意外情况出现的。
!p:如果循环退出时,p的内容为空,说明i给的太大了(很可能超出了链表长度),一直到p为空的时候都没有实现i==j(也有可能p)。
j>i:说明i给小了(例如-1等等),这时while循环由于不满足第二个条件直接退出,但p不是空。
最后用e记录目标元素的内容即可。时间复杂度:O(n)
示例:
int main() {
LinkList L;//约定:LinkList用于声明表,LNode用于声明结点
int n;
cin >> n;
CreateList_R(L, n);
int e;
if (GetElem(L, 5, e))//取出第五个结点数据域的值
cout << e;
else
printf("取出失败!");
return 0;
}7.查找:根据指定数据获取该数据位置序号
int LocateElem(LinkList L, int e)
{
LNode* p;
int j = 1;//只要是跟序号有关的,j永远跟着p走
p = L->next;//p指向首元结点
while (p && p->data != e)
{
p = p->next;
j++;
}
if (p)
return j;
else
return 0;
}(1)while循环条件的理解:当p不为空并且p的数据域不为e的时候,循环执行。也就是说,当p的指针域为e的时候退出循环。
如果p不为空,说明是由于p->data == e而退出循环的,直接输出序号即可。如果p为空,那么查找失败。
时间复杂度:O(n)
示例:
8.单链表的插入
int ListInsert(LinkList& L, int i, int e)//i为插入的位置,e为数据
{
LNode* p;
int j = 0;
p = L;
while (p && j < i - 1)
{
p = p->next;
j++;
}
if (!p || j > i - 1)
{
return 0;
}
LNode* s;
s = new LNode;
s->data = e;
s->next = p->next;
p->next = s;
return 1;
}(1)对插入位置的理解:
即插入的结点是第几个结点(首元结点为第一个,头结点为第0个)
(2)对while循环条件的理解:
想要理解while循环的条件,就必须理解插入的思想:找到插入位置的前一个结点,把他的next值赋给新结点的next域,然后把他的next修改为新结点的地址。因此要先找到i-1位置的结点,如果没有该结点就报错。
当p不为空且j p指向的下一个就是目标位置,因此需要在这里停下。 与查找相同,左边是i给太大了,右边是i给太小了。 需要注意的一点是:初始化条件(p=L,j=0)是不能变的,因为有可能插入在第一个位置,也就是说这时候i-1==0。 时间复杂度:O(1) 示例: (1)如何理解while循环里的内容: 要理解while循环里的内容,首先要理解删除的思想:找到要删除的位置的前一个结点p(i-1),然后把该结点的指针域修改为p->next->next即可(也就是直接跳过了要删除的结点),最后把要删除的结点删除即可。 因此while循环的作用就是找到i-1位置的结点时停下,或者p->next==NULL时也要停下(因为这时已经到了尾结点,还没找到i-1,已经需要报错了) 这里与插入不同的地方:在插入操作中,若i-1为尾结点,则不需要报错,因为可以插入到尾结点后面。但是若删除的操作i-1为尾结点,那么后面已经没有结点可以删除了,需要报错。 (2)如何理解if条件里的内容: 左边说明i-1已经大于等于尾结点,要报错了,右边说明i给小了(0及以下,while直接退出),也需要报错。 (3)核心代码: 让结点指针q指向被删除的结点,把q的指针域(即p->next->next)赋给p的指针域,实现整条链表跳过q直接指向下一个结点。 时间复杂度:O(1) 示例: 声明一个结点指针,从头结点开始,让头结点遍历单链表,一个一个delete(因为p指向的结点删除后,就不能用p=p->next了,因此L需要提前移动)。 需要区分的是销毁单链表和清空单链表的区别:清空单链表保留了头指针和头结点,而销毁单链表则销毁了所有结点。 因为清空单链表保留了头指针和头结点,因此L始终是头结点指针(这点是两者的本质区别),然后定义两个结点指针,一个清空指针p,一个定位指针q,把p后面的结点赋给q,p用于删除,然后再把q赋给p。最后把头结点的指针域置空即可。 空表:链表中无元素,头指针和头结点仍然在。 只要看头结点指针域是否为空即可。 只对输入的单链表进行改进,不创建新的单链表:需要用到三个指针,初始化为—— NULL,首元结点,头结点(画图就行了)。s->data = e;
s->next = p->next;
p->next = s;(3)对if条件的理解:
int main() {
LinkList L;//约定:LinkList用于声明表,LNode用于声明结点
int n;
cout << "请输入链表长度:";
cin >> n;
CreateList_R(L, n);
int e,i;
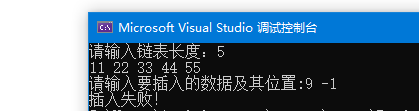
printf("请输入要插入的数据及其位置:");
cin >> e >> i;
if (ListInsert(L, i, e))
{
printf("插入成功!\n");
printf("修改后的链表为:");
LNode* p = L->next;
while (p)
{
printf("%d ", p->data);
p = p->next;
}
}
else
cout << "插入失败!";
return 0;
}9.单链表的删除
int ListDelete(LinkList& L, int i, int& e)
{
LNode *p, *q;
p = L;
int j = 0;
while (p->next!=NULL && j < i-1)
{
p = p->next;
j++;
}
if (p->next==NULL || j > i-1)
{
return 0;
}
q = p->next;
p->next = q->next;
e = q->data;
delete q;//用delete删除结点
return 1;
}q = p->next;
p->next = q->next;int main() {
LinkList L;//约定:LinkList用于声明表,LNode用于声明结点
int n;
cout << "请输入链表长度:";
cin >> n;
CreateList_R(L, n);
int e, i;
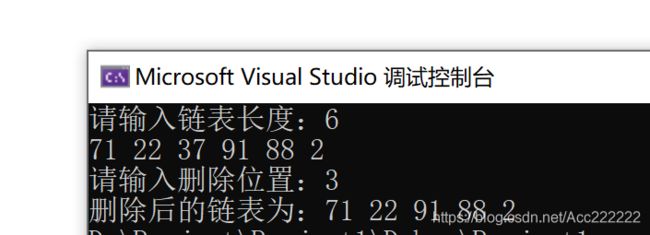
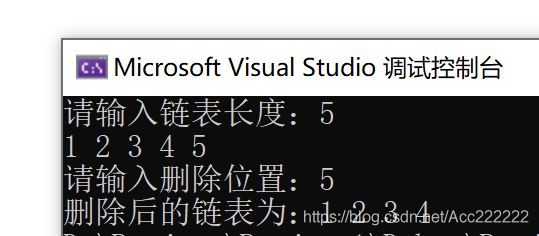
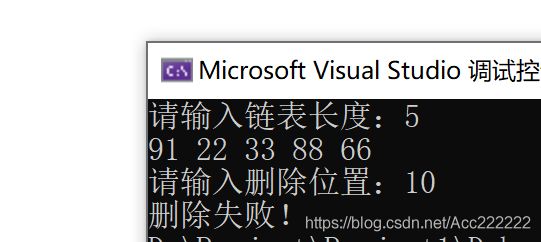
cout << "请输入删除位置:";
cin >> i;
if (ListDelete(L, i, e)) {
cout << "删除后的链表为:";
LNode* p = L->next;
while (p) {
printf("%d ", p->data);
p = p->next;
}
}
else
cout << "删除失败!";
return 0;
}10. 销毁单链表
int DestroyList(LinkList& L)
{
LNode* p;
while (L)
{
p = L;
L = L->next;
delete p;
}
return 1;
}11. 清空单链表
int ClearList(LinkList& L)
{
LNode *p, *q;
p = L->next;
while (p)
{
q = p->next;
delete p;
p = q;
}
L->next = NULL;
return 1;
}12. 判断链表是否为空
int IsEmpty(LinkList L) {
if (L->next)
return 0;//非空
else
return 1;//空
}13. 单链表逆转
int Reverse(LinkList &L) {
LNode* p1 = L->next; //如果没有头结点则直接为L
LNode* p2 = NULL;
while (p1) {
LNode* p = p1->next;
p1->next = p2; //第一个变最后一个 next为NULL
p2 = p1;
p1 = p; //移动到下一个
}//最终p1和p指向null,p2为首元结点
L = p2; // 修改L为逆转后的头指针
}