DFS与BFS寻找图中的所有路径（C++）

图的存储

理论知识

• 图的存储主要有 2 种方式
  1. 邻接表
  2. 邻接矩阵
     邻接矩阵不适合存储稀疏图，本文使用邻接表来存储图
• 邻接表
  • 邻接表用多个链表来表示图，每个链表的头节点表示图中节点，而头结点指向的节点是图中该节点所指向的所有节点
  • 示例
    
    • 节点1指向的节点有 2、3，因此以 1 为头结点的链表，头结点指向的节点是2、3
      需要说明的是，如果没有特殊规定，邻接表的顺序是任意的，例如图中节点1的链表也可以是1 -> 3 -> 2 -> Ø
    • 节点6没有指向其他节点，因此直接指向空

数组模拟链表

// head : 头节点指向的位置
// e[i] : 节点 i 的值
// ne[i] : 节点 i 指向的位置
// idx : 未分配内存的地址 
int head, e[N], ne[N], idx;

// 初始化 
void init()
{
    // -1 表示指向空 
	head = -1;
	idx = 0;
}

// 头插 
void add_at_head(int x)
{
	e[idx] = x;
	ne[idx] = head;
	head = idx++;
}

// 在 k 之后插入值为 x 的节点 
void add(int k, int x)
{
	e[idx] = x;
	ne[idx] = ne[k];
	ne[k] = idx++;
}

// 删除 k 的下一个节点 
void remove(int k)
{
	ne[k] = ne[ne[k]];
}

• 示例
  

数组模拟邻接表

const int N = 1e6 + 10;

/*
	h[i] : 邻接表 i 的下一个节点的【位置】
	h[1] 表示节点 1 的头结点
	
	e[i] : i 节点的值
	ne[i] : i 节点的下一个节点
	st[i] : i 节点是否被访问过 
	idx : 分配节点的位置 
	
*/
int h[N], e[N], ne[N], idx;
bool st[N];

void init()
{
    // -1 表示指向空
	memset(h, -1, sizeof h);
}

// 插入一条 a 指向 b 的有向边 
void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++; 
}

• 示例
  

DFS 寻找所有路径

代码

#include 
#include 
#include 
using namespace std;

const int N = 1e5;
vector<vector<int>> all;
int h[N], e[N], ne[N], idx;
// st[i] : 节点 i 是否被访问过 
bool st[N];


void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}


void dfs(int u, int end, vector<int>& path)
{
	// 标记当前节点已经被访问 
	st[u] = true;
	// 路径添加 u 
	path.push_back(u);
	
	// 已经到达了终点，则保存路径 
	if(u == end)
	{
		all.push_back(path);
		// 标记终点未访问，否则只能输出一条路径 
		st[u] = false;
		return;
	}
	
	// 遍历头结点为 i 的邻接表链表 
	for(int i=h[u]; i!=-1; i=ne[i])
	{
		int j = e[i];
		if(!st[j])
		{
			st[j] = true;
			dfs(j, end, path);
			// dfs 执行完成，需要将添加进路径的元素删除 
			path.pop_back();
		}
	}
	// 已经尝试完了 u 的所有路径，回溯 
	st[u] = false;
}


int main()
{
	// 初始化邻接表 
	memset(h, -1, sizeof h);
	
	// 添加边 
	add(1, 2); add(1, 3);
	add(2, 4);
	add(3, 4);
	add(4, 5);
	add(5, 6);
	
	// 求所有路径 
	vector<int> path;
	dfs(1, 6, path);
	
	// 输出所有路径 
	for(int i=0; i<all.size(); ++i)
	{
		for(int j=0; j<all[i].size(); ++j) 
			cout << all[i][j] << ' ';
		cout << endl;
	}
	
	return 0;
}

输入数据对应图

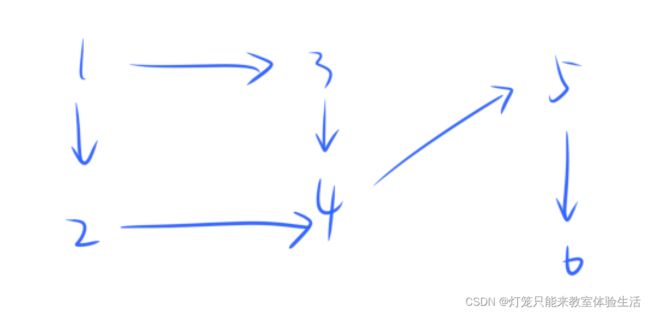
// 添加边 
add(1, 2); add(1, 3);
add(2, 4);
add(3, 4);
add(4, 5);
add(5, 6);

输出

1 3 4 5 6
1 2 4 5 6

BFS 寻找所有路径

代码

#include 
#include 
#include 
#include 
using namespace std;

const int N = 1e5;
vector<vector<int>> all;
int h[N], e[N], ne[N], idx;

void add(int a, int b)
{
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}


void bfs(int start, int end, int n)
{
	// 队列 
	queue<vector<int>> q;
	queue<vector<bool>> q_st;
	q.push({start});
	q_st.push(vector<bool>(n + 1, false));
	while(q.size())
	{
		// 获取队列中的第一条路径 
		vector<int> path = q.front(); q.pop();
		vector<bool> st = q_st.front(); q_st.pop();
		
		// 路径的最后一个元素 
		int last = path.back();
		st[last] = true;
		
		// 若路径的最后一个元素与 end 相等，说明已经找到一条路径，加入 all 
		if(last == end)
		{
			all.push_back(path);
			continue;
		}
		
		// 以当前 path 为基础，加入 last 的所有相邻节点，作为新的路径 
		for(int i=h[last]; i!=-1; i=ne[i])
		{
			int j = e[i];
			if(!st[j])
			{
				
				vector<int> next_path(path);
				next_path.push_back(j);
				
				vector<bool> next_st(st);
				next_st[j] = true;
				
				// 添加该条路径，等待后续 bfs 
				q.push(next_path);
				q_st.push(next_st);
			}
		}
	}
}

int main()
{
	// 初始化邻接表 
	memset(h, -1, sizeof h);
	
	// 添加边 
	add(1, 2); add(1, 3);
	add(2, 4);
	add(3, 4); add(3, 5);
	add(4, 5); add(4, 1);
	add(5, 6);
	
	// 求所有路径 
	vector<int> path;
	bfs(1, 6, 6);
	
	// 输出所有路径 
	for(int i=0; i<all.size(); ++i)
	{
		for(int j=0; j<all[i].size(); ++j) 
			cout << all[i][j] << ' ';
		cout << endl;
	}
	
	return 0;
}

输入数据对应图

// 添加边 
add(1, 2); add(1, 3);
add(2, 4);
add(3, 4); add(3, 5);
add(4, 5); add(4, 1);
add(5, 6);

输出

1 3 5 6
1 3 4 5 6
1 2 4 5 6

备注

• 从输出中可以看出，实际上还有其他的路径，例如：1 -> 3 -> 4 -> 1 -> 3 -> 5 -> 6，
  甚至我们可以在1 - > 3 -> 4 -> 1 这个环中绕上无数圈
• 由于有环的存在，若不判断某节点是否访问，有可能导致死循环
• BFS 求出的所有路径，对于每一条路径而言，是最短路
• 注意到，找到路径时，BFS 并没有标记终点为未访问，为什么呢？

  // 若路径的最后一个元素与 end 相等，说明已经找到一条路径，加入 all 
  if(last == end)
  {
  	// st[last] = false;
  	all.push_back(path);
  	continue;
  }
  

  因为BFS的队列中，保存的是不同的路径和访问情况，因此是否加上st[last] = false 都不影响结果

写在后面

• 若本文代码或思路有误，欢迎指出