程序设计 算法基础
✅作者简介:人工智能专业本科在读,喜欢计算机与编程,写博客记录自己的学习历程。
个人主页:小嗷犬的个人主页
个人网站:小嗷犬的技术小站
个人信条:为天地立心,为生民立命,为往圣继绝学,为万世开太平。
本文目录
-
- 复杂度
-
- 基本操作数
- 时间复杂度
-
- 定义
- 引入
- 渐进符号的定义
-
- 大 Θ 符号
- 大 O 符号
- 大 Ω 符号
- 小 o 符号
- 小 ω 符号
- 常见性质
- 简单的时间复杂度计算的例子
-
- for 循环
- DFS
- 哪些量是常量?
- 主定理 (Master Theorem)
-
- 证明
- 应用
- 空间复杂度
- 枚举
-
- 简介
- 要点
-
- 给出解空间
- 减少枚举的空间
- 选择合适的枚举顺序
- 例题
-
- 题目描述
- 解题思路
- 复杂度分析
- 模拟
-
- 简介
- 技巧
- 例题
-
- 题目描述
- 解题思路
- 递归 & 分治
-
- 递归
-
- 定义
- 引入
- 为什么要写递归
- 递归的缺点
- 递归的优化
-
- 剪枝
- 尾递归
- 记忆化搜索
- 分治
-
- 定义
- 过程
- 要点
-
- 写递归的要点
- 区别
-
- 递归与枚举的区别
- 递归与分治的区别
- 例题
-
- 题目描述
- 解题思路
- 贪心
-
- 引入
- 解释
-
- 适用范围
- 证明
- 要点
-
- 常见题型
- 排序解法
- 后悔解法
- 区别
-
- 与动态规划的区别
- 例题
-
- 邻项交换法的例题
-
- 解题思路
- 后悔法的例题
-
- 解题思路
- 参考代码
- 复杂度分析
- 排序
-
- 定义
- 性质
-
- 稳定性
- 时间复杂度
- 空间复杂度
- 常见排序算法对比
- STL 中的排序
-
- 内省排序
-
- 定义
- 性质
- 实现
- 应用
-
- 理解数据的特点
- 降低时间复杂度
- 作为查找的预处理
- 前缀和 & 差分
-
- 前缀和
-
- 定义
- 例题
-
- 题目描述
- 解题思路
- 参考代码
- 二维/多维前缀和
-
- 例题
- 其他
- 差分
-
- 解释
- 性质
- 二分
-
- 二分法
-
- 定义
- 过程
- 性质
-
- 时间复杂度
- 空间复杂度
- 实现
- 最大值最小化
- STL 的二分查找
- 二分答案
-
- 例题描述
- 解题思路
- 参考代码
- 三分法
-
- 引入
- 实现
-
- 伪代码
- C++
- 例题
-
- 题目描述
- 解题思路
- 参考代码
- 倍增
-
- 定义
- 应用
-
- RMQ 问题
- 树上倍增求 LCA
- 例题
-
- 题目描述
- 解题思路
- 构造
-
- 引入
- 特点
- 例题1
-
- 题目描述
- 解题思路
- 例题2
-
- 题目描述
- 解题思路
复杂度
时间复杂度和空间复杂度是衡量一个算法效率的重要标准。
基本操作数
同一个算法在不同的计算机上运行的速度会有一定的差别,并且实际运行速度难以在理论上进行计算,实际去测量又比较麻烦,所以我们通常考虑的不是算法运行的实际用时,而是算法运行所需要进行的基本操作的数量。
在普通的计算机上,加减乘除、访问变量(基本数据类型的变量,下同)、给变量赋值等都可以看作基本操作。
对基本操作的计数或是估测可以作为评判算法用时的指标。
时间复杂度
定义
衡量一个算法的快慢,一定要考虑数据规模的大小。所谓数据规模,一般指输入的数字个数、输入中给出的图的点数与边数等等。一般来说,数据规模越大,算法的用时就越长。而在算法竞赛中,我们衡量一个算法的效率时,最重要的不是看它在某个数据规模下的用时,而是看它的用时随数据规模而增长的趋势,即 时间复杂度。
引入
考虑用时随数据规模变化的趋势的主要原因有以下几点:
- 现代计算机每秒可以处理数亿乃至更多次基本运算,因此我们处理的数据规模通常很大。如果算法 A 在规模为 n n n 的数据上用时为 100 n 100n 100n 而算法 B 在规模为 n n n 的数据上用时为 n 2 n^2 n2,在数据规模小于 100 100 100 时算法 B 用时更短,但在一秒钟内算法 A 可以处理数百万规模的数据,而算法 B 只能处理数万规模的数据。在允许算法执行时间更久时,时间复杂度对可处理数据规模的影响就会更加明显,远大于同一数据规模下用时的影响。
- 我们采用基本操作数来表示算法的用时,而不同的基本操作实际用时是不同的,例如加减法的用时远小于除法的用时。计算时间复杂度而忽略不同基本操作之间的区别以及一次基本操作与十次基本操作之间的区别,可以消除基本操作间用时不同的影响。
当然,算法的运行用时并非完全由输入规模决定,而是也与输入的内容相关。所以,时间复杂度又分为几种,例如:
- 最坏时间复杂度,即每个输入规模下用时最长的输入对应的时间复杂度。在算法竞赛中,由于输入可以在给定的数据范围内任意给定,我们为保证算法能够通过某个数据范围内的任何数据,一般考虑最坏时间复杂度。
- 平均(期望)时间复杂度,即每个输入规模下所有可能输入对应用时的平均值的复杂度(随机输入下期望用时的复杂度)。
所谓「用时随数据规模而增长的趋势」是一个模糊的概念,我们需要借助下文所介绍的 渐进符号 来形式化地表示时间复杂度。
渐进符号的定义
渐进符号是函数的阶的规范描述。简单来说,渐进符号忽略了一个函数中增长较慢的部分以及各项的系数(在时间复杂度相关分析中,系数一般被称作「常数」),而保留了可以用来表明该函数增长趋势的重要部分。
一个简单的记忆方法是,含等于(非严格)用大写,不含等于(严格)用小写,相等是 Θ \Theta Θ,小于是 O O O,大于是 Ω \Omega Ω。大 O O O 和小 o o o 原本是希腊字母 Omicron,由于字形相同,也可以理解为拉丁字母的大 O O O 和小 o o o。
在英文中,词根「-micro-」和「-mega-」常用于表示 10 的负六次方(百万分之一)和六次方(百万),也表示「小」和「大」。小和大也是希腊字母 Omicron 和 Omega 常表示的含义。
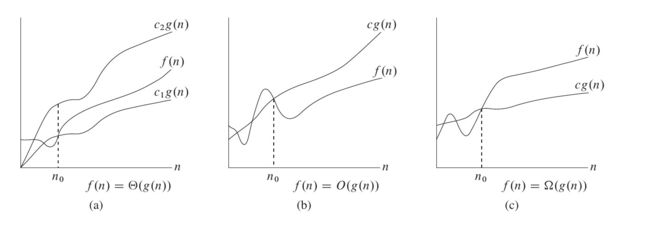
大 Θ 符号
对于函数 f ( n ) f(n) f(n) 和 g ( n ) g(n) g(n)
f ( n ) = Θ ( g ( n ) ) f(n)=\Theta(g(n)) f(n)=Θ(g(n))
当且仅当
∃ c 1 , c 2 , n 0 > 0 \exists c_1,c_2,n_0>0 ∃c1,c2,n0>0
使得
∀ n ≥ n 0 , 0 ≤ c 1 ⋅ g ( n ) ≤ f ( n ) ≤ c 2 ⋅ g ( n ) \forall n \ge n_0, 0\le c_1\cdot g(n)\le f(n) \le c_2\cdot g(n) ∀n≥n0,0≤c1⋅g(n)≤f(n)≤c2⋅g(n)
也就是说,如果函数 f ( n ) = Θ ( g ( n ) ) f(n)=\Theta(g(n)) f(n)=Θ(g(n)),那么我们能找到两个正数 c 1 , c 2 c_1, c_2 c1,c2 使得 f ( n ) f(n) f(n) 被 c 1 ⋅ g ( n ) c_1\cdot g(n) c1⋅g(n) 和 c 2 ⋅ g ( n ) c_2\cdot g(n) c2⋅g(n) 夹在中间。
例如:
- 3 n 2 + 5 n − 3 = Θ ( n 2 ) 3n^2+5n-3=\Theta(n^2) 3n2+5n−3=Θ(n2)
这里的 c 1 , c 2 , n 0 c_1, c_2, n_0 c1,c2,n0 可以分别是 2 , 4 , 100 2, 4, 100 2,4,100。 - n n + n log 5 n + m log m + n m = Θ ( n n + m log m + n m ) n\sqrt {n} + n{\log^5 n} + m{\log m} +nm=\Theta(n\sqrt {n} + m{\log m} + nm) nn+nlog5n+mlogm+nm=Θ(nn+mlogm+nm)
这里的 c 1 , c 2 , n 0 c_1, c_2, n_0 c1,c2,n0 可以分别是 1 , 2 , 100 1, 2, 100 1,2,100。
大 O 符号
Θ \Theta Θ 符号同时给了我们一个函数的上下界,如果只知道一个函数的渐进上界而不知道其渐进下界,可以使用 O O O 符号。
f ( n ) = O ( g ( n ) ) f(n)=O(g(n)) f(n)=O(g(n))
当且仅当
∃ c , n 0 \exists c,n_0 ∃c,n0
使得
∀ n ≥ n 0 , 0 ≤ f ( n ) ≤ c ⋅ g ( n ) \forall n \ge n_0,0\le f(n)\le c\cdot g(n) ∀n≥n0,0≤f(n)≤c⋅g(n)
研究时间复杂度时通常会使用 O O O 符号,因为我们关注的通常是程序用时的上界,而不关心其用时的下界。
需要注意的是,这里的「上界」和「下界」是对于函数的变化趋势而言的,而不是对算法而言的。算法用时的上界对应的是「最坏时间复杂度」而非大 O O O 记号。所以,使用 Θ \Theta Θ 记号表示最坏时间复杂度是完全可行的,甚至可以说 Θ \Theta Θ 比 O O O 更加精确,而使用 O O O 记号的主要原因,一是我们有时只能证明时间复杂度的上界而无法证明其下界(这种情况一般出现在较为复杂的算法以及复杂度分析),二是 O O O 在电脑上输入更方便一些。
大 Ω 符号
同样的,我们使用 Ω \Omega Ω 符号来描述一个函数的渐进下界。
f ( n ) = Ω ( g ( n ) ) f(n)=\Omega(g(n)) f(n)=Ω(g(n))
当且仅当
∃ c , n 0 \exists c,n_0 ∃c,n0
使得
∀ n ≥ n 0 , 0 ≤ c ⋅ g ( n ) ≤ f ( n ) \forall n \ge n_0,0\le c\cdot g(n)\le f(n) ∀n≥n0,0≤c⋅g(n)≤f(n)
小 o 符号
如果说 O O O 符号相当于小于等于号,那么 o o o 符号就相当于小于号。
小 o o o 符号大量应用于数学分析中,函数在某点处的泰勒展开式拥有佩亚诺余项,使用小 o o o 符号表示严格小于,从而进行等价无穷小的渐进分析。
f ( n ) = o ( g ( n ) ) f(n)=o(g(n)) f(n)=o(g(n))
当且仅当对于任意给定的正数
c , ∃ n 0 c,\exists n_0 c,∃n0
使得
∀ n ≥ n 0 , 0 ≤ f ( n ) < c ⋅ g ( n ) \forall n \ge n_0,0\le f(n)< c\cdot g(n) ∀n≥n0,0≤f(n)<c⋅g(n)
小 ω 符号
如果说 Ω \Omega Ω 符号相当于大于等于号,那么 ω \omega ω 符号就相当于大于号。
f ( n ) = ω ( g ( n ) ) f(n)=\omega(g(n)) f(n)=ω(g(n))
当且仅当对于任意给定的正数
c , ∃ n 0 c,\exists n_0 c,∃n0
使得
∀ n ≥ n 0 , 0 ≤ c ⋅ g ( n ) < f ( n ) \forall n \ge n_0,0\le c\cdot g(n)< f(n) ∀n≥n0,0≤c⋅g(n)<f(n)
常见性质
- f ( n ) = Θ ( g ( n ) ) ⟺ f ( n ) = O ( g ( n ) ) ∧ f ( n ) = Ω ( g ( n ) ) f(n) = \Theta(g(n))\iff f(n)=O(g(n))\land f(n)=\Omega(g(n)) f(n)=Θ(g(n))⟺f(n)=O(g(n))∧f(n)=Ω(g(n))
- f 1 ( n ) + f 2 ( n ) = O ( max ( f 1 ( n ) , f 2 ( n ) ) ) f_1(n) + f_2(n) = O(\max(f_1(n), f_2(n))) f1(n)+f2(n)=O(max(f1(n),f2(n)))
- f 1 ( n ) × f 2 ( n ) = O ( f 1 ( n ) × f 2 ( n ) ) f_1(n) \times f_2(n) = O(f_1(n) \times f_2(n)) f1(n)×f2(n)=O(f1(n)×f2(n))
- ∀ a ≠ 1 , log a n = O ( log 2 n ) \forall a \neq 1, \log_a{n} = O(\log_2 n) ∀a=1,logan=O(log2n)。
由换底公式可以得知,任何对数函数无论底数为何,都具有相同的增长率,因此渐进时间复杂度中对数的底数一般省略不写。
简单的时间复杂度计算的例子
for 循环
int n, m;
cin >> n >> m;
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
for (int k = 0; k < m; ++k)
cout << "Hello SWUFE!" << endl;
如果以输入的数值 n n n 和 m m m 的大小作为数据规模,则上面这段代码的时间复杂度为 Θ ( n 2 m ) \Theta(n^2m) Θ(n2m)。
DFS
在对一张 n n n 个点 m m m 条边的图进行 DFS 时,由于每个节点和每条边都只会被访问常数次,复杂度为 Θ ( n + m ) \Theta(n+m) Θ(n+m)。
哪些量是常量?
当我们要进行若干次操作时,如何判断这若干次操作是否影响时间复杂度呢?例如:
const int N = 100000;
for (int i = 0; i < N; ++i)
cout << "Hello SWUFE!" << endl;
如果 N N N 的大小不被看作输入规模,那么这段代码的时间复杂度就是 O ( 1 ) O(1) O(1)。
进行时间复杂度计算时,哪些变量被视作输入规模是很重要的,而所有和输入规模无关的量都被视作常量,计算复杂度时可当作 1 1 1 来处理。
需要注意的是,在进行时间复杂度相关的理论性讨论时,「算法能够解决任何规模的问题」是一个基本假设(当然,在实际中,由于时间和存储空间有限,无法解决规模过大的问题)。因此,能在常量时间内解决数据规模有限的问题(例如,对于数据范围内的每个可能输入预先计算出答案)并不能使一个算法的时间复杂度变为 O ( 1 ) O(1) O(1)。
主定理 (Master Theorem)
我们可以使用 Master Theorem 来快速求得关于递归算法的复杂度。 Master Theorem 递推关系式如下
T ( n ) = a T ( n b ) + f ( n ) ∀ n > b T(n) = a T\left(\frac{n}{b}\right)+f(n)\quad \forall n > b T(n)=aT(bn)+f(n)∀n>b
那么
T ( n ) = { Θ ( n log b a ) f ( n ) = O ( n log b a − ϵ ) , ϵ > 0 Θ ( f ( n ) ) f ( n ) = Ω ( n log b a + ϵ ) , ϵ ≥ 0 Θ ( n log b a log k + 1 n ) f ( n ) = Θ ( n log b a log k n ) , k ≥ 0 T(n) = \begin{cases}\Theta(n^{\log_b a}) & f(n) = O(n^{\log_b a-\epsilon}),\epsilon > 0 \\ \Theta(f(n)) & f(n) = \Omega(n^{\log_b a+\epsilon}),\epsilon\ge 0\\ \Theta(n^{\log_b a}\log^{k+1} n) & f(n)=\Theta(n^{\log_b a}\log^k n),k\ge 0 \end{cases} T(n)=⎩ ⎨ ⎧Θ(nlogba)Θ(f(n))Θ(nlogbalogk+1n)f(n)=O(nlogba−ϵ),ϵ>0f(n)=Ω(nlogba+ϵ),ϵ≥0f(n)=Θ(nlogbalogkn),k≥0
需要注意的是,这里的第二种情况还需要满足正则条件,即对于某些常数 c < 1 c < 1 c<1 和足够大的 n n n,有 a f ( n / b ) ≤ c f ( n ) a f(n/b) \leq c f(n) af(n/b)≤cf(n)。
证明思路是是将规模为 n n n 的问题,分解为 a a a 个规模为 ( n b ) (\frac{n}{b}) (bn) 的问题,然后依次合并,直到合并到最高层。每一次合并子问题,都需要花费 f ( n ) f(n) f(n) 的时间。
证明
依据上文提到的证明思路,具体证明过程如下
对于第 0 0 0 层(最高层),合并子问题需要花费 f ( n ) f(n) f(n) 的时间
对于第 1 1 1 层(第一次划分出来的子问题),共有 a a a 个子问题,每个子问题合并需要花费 f ( n b ) f\left(\frac{n}{b}\right) f(bn) 的时间,所以合并总共要花费 a f ( n b ) a f\left(\frac{n}{b}\right) af(bn) 的时间。
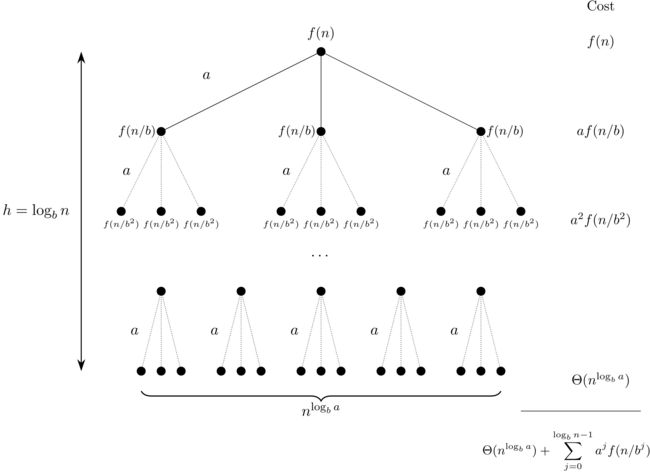
层层递推,我们可以写出类推树如下:
这棵树的高度为 log b n {\log_b n} logbn,共有 n log b a n^{\log_b a} nlogba 个叶子,从而 T ( n ) = Θ ( n log b a ) + g ( n ) T(n) = \Theta(n^{\log_b a}) + g(n) T(n)=Θ(nlogba)+g(n),其中 g ( n ) = ∑ j = 0 log b n − 1 a j f ( n / b j ) g(n) = \sum_{j = 0}^{\log_{b}{n - 1}} a^{j} f(n / b^{j}) g(n)=∑j=0logbn−1ajf(n/bj)。
针对于第一种情况: f ( n ) = O ( n log b a − ϵ ) f(n) = O(n^{\log_b a-\epsilon}) f(n)=O(nlogba−ϵ),因此 g ( n ) = O ( n log b a ) g(n) = O(n^{\log_b a}) g(n)=O(nlogba)。
对于第二种情况而言:首先 g ( n ) = Ω ( f ( n ) ) g(n) = \Omega(f(n)) g(n)=Ω(f(n)),又因为 a f ( n b ) ≤ c f ( n ) a f(\dfrac{n}{b}) \leq c f(n) af(bn)≤cf(n),只要 c c c 的取值是一个足够小的正数,且 n n n 的取值足够大,因此可以推导出: g ( n ) = O ( f ( n ) ) g(n) = O(f(n)) g(n)=O(f(n))。两侧夹逼可以得出, g ( n ) = Θ ( f ( n ) ) g(n) = \Theta(f(n)) g(n)=Θ(f(n))。
而对于第三种情况: f ( n ) = Θ ( n log b a ) f(n) = \Theta(n^{\log_b a}) f(n)=Θ(nlogba),因此 g ( n ) = O ( n log b a log n ) g(n) = O(n^{\log_b a} {\log n}) g(n)=O(nlogbalogn)。 T ( n ) T(n) T(n) 的结果可在 g ( n ) g(n) g(n) 得出后显然得到。
应用
下面举几个例子来说明主定理如何使用。
例如:
- T ( n ) = T ( n 2 ) + 1 T(n) = T\left(\frac{n}{2}\right) + 1 T(n)=T(2n)+1,
那么 a = 1 , b = 2 , log 2 1 = 0 a=1, b=2, {\log_2 1} = 0 a=1,b=2,log21=0,那么 ϵ \epsilon ϵ 可以取值为 0 0 0,
从而满足第一种情况,所以 T ( n ) = Θ ( log n ) T(n) = \Theta(\log n) T(n)=Θ(logn)。 - T ( n ) = T ( n 2 ) + n T(n) = T\left(\frac{n}{2}\right) + n T(n)=T(2n)+n,
那么 a = 1 , b = 2 , log 2 1 = 0 a=1, b=2, {\log_2 1} = 0 a=1,b=2,log21=0,那么 ϵ \epsilon ϵ 可以取值为 0.5 0.5 0.5,
从而满足第二种情况,所以 T ( n ) = Θ ( n ) T(n) = \Theta(n) T(n)=Θ(n)。 - T ( n ) = T ( n 2 ) + log n T(n) = T\left(\frac{n}{2}\right) + {\log n} T(n)=T(2n)+logn,
那么 a = 1 , b = 2 , log 2 1 = 0 a=1, b=2, {\log_2 1}=0 a=1,b=2,log21=0,那么 k k k 可以取值为 1 1 1,
从而满足第三种情况,所以 T ( n ) = Θ ( log 2 n ) T(n) = \Theta(\log^2 n) T(n)=Θ(log2n)。
空间复杂度
类似地,算法所使用的空间随输入规模变化的趋势可以用 空间复杂度 来衡量。
枚举
简介
枚举(英语:Enumerate)是基于已有知识来猜测答案的一种问题求解策略。
枚举的思想是不断地猜测,从可能的集合中一一尝试,然后再判断题目的条件是否成立。
要点
给出解空间
建立简洁的数学模型。
枚举的时候要想清楚:可能的情况是什么?要枚举哪些要素?
减少枚举的空间
枚举的范围是什么?是所有的内容都需要枚举吗?
在用枚举法解决问题的时候,一定要想清楚这两件事,否则会带来不必要的时间开销。
选择合适的枚举顺序
根据题目判断。比如例题中要求的是最大的符合条件的素数,那自然是从大到小枚举比较合适。
例题
以下是一个使用枚举解题与优化枚举范围的例子。
题目描述
一个数组中的数互不相同,求其中和为 0 0 0 的数对的个数。
解题思路
枚举两个数的代码很容易就可以写出来。
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j)
if (a[i] + a[j] == 0) ++ans;
来看看枚举的范围如何优化。由于题中没要求数对是有序的,答案就是有序的情况的两倍(考虑如果 (a, b) 是答案,那么 (b, a) 也是答案)。对于这种情况,只需统计人为要求有顺序之后的答案,最后再乘上 2 2 2 就好了。
不妨要求第一个数要出现在靠前的位置。代码如下:
for (int i = 0; i < n; ++i)
for (int j = 0; j < i; ++j)
if (a[i] + a[j] == 0) ++ans;
ans *= 2;
不难发现这里已经减少了 j j j 的枚举范围,减少了这段代码的时间开销。
我们可以在此之上进一步优化。
两个数是否都一定要枚举出来呢?枚举其中一个数之后,题目的条件已经确定了其他的要素(另一个数)的条件,如果能找到一种方法直接判断题目要求的那个数是否存在,就可以省掉枚举后一个数的时间了。较为进阶地,在数据范围允许的情况下,我们可以使用 set 记录遍历过的数。
set<int> s;
for (int i = 0; i < n; ++i)
{
if (s.count(-a[i])) ++ans;
s.insert(a[i]);
}
ans *= 2;
复杂度分析
- 时间复杂度: O ( n ) O(n) O(n),对数组 a a a 进行了一次遍历。
- 空间复杂度: O ( n ) O(n) O(n)
模拟
简介
模拟就是用计算机来模拟题目中要求的操作。
模拟题目通常具有码量大、操作多、思路繁复的特点。由于它码量大,经常会出现难以查错的情况,如果在考试中写错是相当浪费时间的。
技巧
写模拟题时,遵循以下的建议有可能会提升做题速度:
- 在动手写代码之前,在草稿纸上尽可能地写好要实现的流程。
- 在代码中,尽量把每个部分模块化,写成函数、结构体或类。
- 对于一些可能重复用到的概念,可以统一转化,方便处理:如,某题给你 “YY-MM-DD 时:分” 把它抽取到一个函数,处理成秒,会减少概念混淆。
- 调试时分块调试。模块化的好处就是可以方便的单独调某一部分。
- 写代码的时候一定要思路清晰,不要想到什么写什么,要按照落在纸上的步骤写。
实际上,上述步骤在解决其它类型的题目时也是很有帮助的。
例题
题目描述
一只长度不计的蠕虫位于 n n n 英寸深的井的底部。它每次向上爬 u u u 英寸,但是必须休息一次才能再次向上爬。在休息的时候,它滑落了 d d d 英寸。之后它将重复向上爬和休息的过程。蠕虫爬出井口需要至少爬多少次?如果蠕虫爬完后刚好到达井的顶部,我们也设作蠕虫已经爬出井口。
解题思路
直接使用程序模拟蠕虫爬井的过程就可以了。用一个循环重复蠕虫的爬井过程,当攀爬的长度超过或者等于井的深度时跳出。
#include 递归 & 分治
本章将介绍递归与分治算法的区别与结合运用。
递归
定义
递归(英语:Recursion),在数学和计算机科学中是指在函数的定义中使用函数自身的方法,在计算机科学中还额外指一种通过重复将问题分解为同类的子问题而解决问题的方法。
引入
要理解递归,就得先理解什么是递归。
递归的基本思想是某个函数直接或者间接地调用自身,这样原问题的求解就转换为了许多性质相同但是规模更小的子问题。求解时只需要关注如何把原问题划分成符合条件的子问题,而不需要过分关注这个子问题是如何被解决的。
以下是一些有助于理解递归的例子:
递归在数学中非常常见。例如,集合论对自然数的正式定义是:1 是一个自然数,每个自然数都有一个后继,这一个后继也是自然数。
递归代码最重要的两个特征:结束条件和自我调用。自我调用是在解决子问题,而结束条件定义了最简子问题的答案。
int func(传入数值)
{
if (终止条件) return 最小子问题解;
return func(缩小规模);
}
为什么要写递归
-
结构清晰,可读性强。例如,分别用不同的方法实现归并排序:
using namespace std; // 不使用递归的归并排序算法 template <typename T> void merge_sort(vector<T> a) { int n = a.size(); for (int seg = 1; seg < n; seg = seg + seg) for (int start = 0; start < n - seg; start += seg + seg) merge(a, start, start + seg - 1, min(start + seg + seg - 1, n - 1)); } // 使用递归的归并排序算法 template <typename T> void merge_sort(vector<T> a, int front, int end) { if (front >= end) return; int mid = front + (end - front) / 2; merge_sort(a, front, mid); merge_sort(a, mid + 1, end); merge(a, front, mid, end); }显然,递归版本比非递归版本更易理解。递归版本的做法一目了然:把左半边排序,把右半边排序,最后合并两边。而非递归版本看起来不知所云,充斥着各种难以理解的边界计算细节,特别容易出 bug,且难以调试。
-
练习分析问题的结构。当发现问题可以被分解成相同结构的小问题时,递归写多了就能敏锐发现这个特点,进而高效解决问题。
递归的缺点
在程序执行中,递归是利用堆栈来实现的。每当进入一个函数调用,栈就会增加一层栈帧,每次函数返回,栈就会减少一层栈帧。而栈不是无限大的,当递归层数过多时,就会造成 栈溢出 的后果。
显然有时候递归处理是高效的,比如归并排序;有时候是低效的,比如数孙悟空身上的毛,因为堆栈会消耗额外空间,而简单的递推不会消耗空间。比如这个例子,给一个链表头,计算它的长度:
// 典型的递推遍历框架
int size(Node *head)
{
int size = 0;
for (Node *p = head; p != nullptr; p = p->next)
size++;
return size;
}
// 我就是要写递归,递归天下第一
int size_recursion(Node *head)
{
if (head == nullptr)
return 0;
return size_recursion(head->next) + 1;
}
递归的优化
递归的优化主要有 3 种方法:剪枝、尾递归和记忆化搜索。
剪枝
剪枝是指在递归的过程中,根据题目的要求,提前判断某些情况,从而减少递归的次数。
通常分为以下几种情况:
- 可行性剪枝:所谓可行性剪枝,就是如当前状态和题意不符,并且由于题目可以推出,往后的所有情况和题意都不符,那么就可以进行剪枝,直接把这种情况及后续的所有情况判负,直接返回。
- 排除等效冗余:所谓排除等效冗余,就是当几个枝桠具有完全相同的效果的时候,只选择其中一个走就可以了。
- 最优性剪枝:所谓最优性剪枝,是在我们用搜索方法解决最优化问题的时候的一种常用剪枝方法。当搜到一半的时候,发现比已经搜索到的最优解差,则该方案肯定是不行的,即刻停止搜索,进行回溯。
- 顺序剪枝:普遍来讲,搜索的顺序是不固定的,对一个问题来讲,算法可以进入搜索树的任意的一个子节点。但假如我们要搜索一个最小值,而非要从最大值存在的那个节点开搜,就可能存在搜索到最后才出解。而我们从最小的节点开搜很可能马上就出解。这就是顺序剪枝的一个应用。一般来讲,有单调性存在的搜索问题可以和贪心思想结合,进行顺序剪枝。
尾递归
尾递归是指在递归的过程中,递归调用是函数的最后一步操作。
当我们用递归的形式写一个计算阶乘的函数,我们大概会这么写:
int fact(int n)
{
if (n <= 1)
return 1;
else
return n * fact(n - 1);
}
当我们计算 fact(6) 的时候,会产生如下展开:
fact(6)
6 * fact(5)
6 * (5 * fact(4))
6 * (5 * (4 * fact(3)))
// two thousand years later...
6 * (5 * (4 * (3 * (2 * 1)))) // <= 最终的展开
注意了,到这里为止,程序做的仅仅还只是展开而已,并没有运算真正运运算,接下来才是运算:
6 * (5 * (4 * (3 * (2 * 1))))
6 * (5 * (4 * (3 * 2)))
6 * (5 * (4 * 6))
// two thousand years later...
720 // <= 最终的结果
我们普通递归的问题在于展开的时候会产生非常大的中间缓存,而每一层的中间缓存都会占用我们宝贵的栈空间,所有导致了当 n n n 很大的时候,栈空间不足则会产生栈溢出的情况。
尾递归则能够一定程度上解决这个问题。我们可以把上面的代码改写成尾递归的形式:
int fact(int n, int result = 1)
{
if (n <= 1)
return result;
else
return fact(n - 1, n * result);
}
我们像上面一个普通递归函数一样来展开和运算 fact(6):
fact(6, 1)
fact(5, 6)
fact(4, 30)
fact(3, 120)
fact(2, 360)
fact(1, 720)
720 // <= 最终的结果
跟上面的普通递归函数比起来,貌似尾递归函数因为在展开的过程中计算并且缓存了结果,使得并不会像普通递归函数那样展开出非常庞大的中间结果,所以不会产生栈溢出对吗?
答案是否定的,尾递归函数依然还是递归函数,如果不优化依然跟普通递归函数一样会出现栈溢出。
尾递归函数的优化是依赖于编译器的,编译器会对尾递归函数进行优化,把尾递归函数转换成迭代函数,从而避免了中间结果的缓存,也就避免了栈溢出的问题。
普通递归和尾递归的区别在于:普通递归需要保留入口环境,让我们可以在函数回溯后进行其他操作,而尾递归最后一步是直接返回,不需要进行其他操作,所以不需要保留入口环境。
普通递归是真真正正需要一个栈空间来保存每一层级的入口环境的,而尾递归更像是一个写成递归形式的迭代函数。
记忆化搜索
记忆化搜索是指在递归的过程中,将已经计算过的结果保存下来,当再次遇到相同的情况时,直接返回结果,从而减少递归的次数。
记忆化搜索的核心思想是空间换时间,通过增加空间复杂度来降低时间复杂度。(事实上,由于记忆化搜索减少了递归的次数,所以空间复杂度并不一定会比原来高)
当我们用普通递归实现一个计算斐波那契数列第 n n n 项的函数时,我们可能会这么写:
long long fib(int n)
{
if (n <= 1)
return n;
else
return fib(n - 1) + fib(n - 2);
}
我们使用下面的程序来给这个函数计时:
#include 输出的结果为:
fib(40) = 102334155
time = 0.495s
用时这么长的原因是:在我们计算 fib(40) 的时候,程序会递归调用 fib(39) 和 fib(38),而 fib(39) 又会递归调用 fib(38) 和 fib(37),以此类推,我们可以画出递归树:
fib(40)
├── fib(39)
│ ├── fib(38)
│ │ ├── fib(37)
······
│ │ └── fib(36)
│ └── fib(37)
│ ├── fib(36)
······
│ └── fib(35)
└── fib(38)
├── fib(37)
│ ├── fib(36)
······
│ └── fib(35)
└── fib(36)
├── fib(35)
······
可以看出,我们在计算 fib(40) 的时候,会重复计算很多次 fib(38)、fib(37)、fib(36)、fib(35) 等等,这就是重叠子问题。
对于这些需要重复计算的子问题,我们可以使用记忆化搜索来优化。
我们可以使用一个数组 f 来保存已经计算过的结果,当我们需要计算 fib(n) 的时候,先查看 f[n] 是否已经计算过,如果已经计算过,直接返回 f[n],否则计算 fib(n) 并保存到 f[n] 中。
long long f[1000]; // 用来保存已经计算过的结果
long long fib(int n)
{
if (n <= 1)
return n;
else if (f[n] != 0)
return f[n];
else
return f[n] = fib(n - 1) + fib(n - 2);
}
计时程序的输出结果为:
fib(40) = 102334155
time = 0s
可以看到,使用了记忆化搜索之后,对 fib(40) 的计算速度优化非常大。
感兴趣的同学可以用两个程序分别计算 fib(50),感觉一下两者的计算时间差异。
分治
定义
分治(英语:Divide and Conquer),字面上的解释是「分而治之」,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
过程
分治算法的核心思想就是「分而治之」。
大概的流程可以分为三步:分解 -> 解决 -> 合并。
- 分解原问题为结构相同的子问题。
- 分解到某个容易求解的边界之后,进行递归求解。
- 将子问题的解合并成原问题的解。
分治法能解决的问题一般有如下特征:
- 该问题的规模缩小到一定的程度就可以容易地解决。
- 该问题可以分解为若干个规模较小的相同问题,即该问题具有最优子结构性质,利用该问题分解出的子问题的解可以合并为该问题的解。
- 该问题所分解出的各个子问题是相互独立的,即子问题之间不包含公共的子问题。
以归并排序为例。假设实现归并排序的函数名为 merge_sort。明确该函数的职责,即 对传入的一个数组排序。这个问题显然可以分解。给一个数组排序等于给该数组的左右两半分别排序,然后合并成一个数组。
void merge_sort(一个数组)
{
if (可以很容易处理) return;
merge_sort(左半个数组);
merge_sort(右半个数组);
merge(左半个数组, 右半个数组);
}
传给它半个数组,那么处理完后这半个数组就已经被排好了。注意到,merge_sort 与二叉树的后序遍历模板极其相似。因为分治算法的套路是 分解 -> 解决(触底)-> 合并(回溯),先左右分解,再处理合并,回溯就是在退栈,即相当于后序遍历。
merge 函数的实现方式与两个有序链表的合并一致。
要点
写递归的要点
明白一个函数的作用并相信它能完成这个任务,千万不要跳进这个函数里面企图探究更多细节,否则就会陷入无穷的细节无法自拔,人脑能压几个栈啊。
以遍历二叉树为例。
void traverse(TreeNode* root)
{
if (root == nullptr) return;
traverse(root->left);
traverse(root->right);
}
这几行代码就足以遍历任何一棵二叉树了。对于递归函数 traverse(root),只要相信给它一个根节点 root,它就能遍历这棵树。所以只需要把这个节点的左右节点再传给这个函数就行了。
同样扩展到遍历一棵 N 叉树。与二叉树的写法一模一样。
void traverse(TreeNode* root)
{
if (root == nullptr) return;
for (auto child : root->children) traverse(child);
}
区别
递归与枚举的区别
递归和枚举的区别在于:枚举是横向地把问题划分,然后依次求解子问题;而递归是把问题逐级分解,是纵向的拆分。
递归与分治的区别
递归是一种编程技巧,一种解决问题的思维方式;分治算法很大程度上是基于递归的,解决更具体问题的算法思想。
例题
题目描述
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过 1000 1000 1000 个节点,且节点数值范围是 [ − 1000000 , 1000000 ] [-1000000,1000000] [−1000000,1000000] 的整数。
示例:
root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8
10
/ \
5 -3
/ \ \
3 2 11
/ \ \
3 -2 1
返回 3。和等于 8 的路径有:
1. 5 -> 3
2. 5 -> 2 -> 1
3. -3 -> 11
// 二叉树结点的定义
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
解题思路
题目看起来很复杂,不过代码却极其简洁。
首先明确,递归求解树的问题必然是要遍历整棵树的,所以二叉树的遍历框架(分别对左右子树递归调用函数本身)必然要出现在主函数 pathSum 中。那么对于每个节点,它们应该干什么呢?它们应该看看,自己和它们的子树包含多少条符合条件的路径。好了,这道题就结束了。
按照前面说的技巧,根据刚才的分析来定义清楚每个递归函数应该做的事:
PathSum 函数:给定一个节点和一个目标值,返回以这个节点为根的树中,和为目标值的路径总数。
count 函数:给定一个节点和一个目标值,返回以这个节点为根的树中,能凑出几个以该节点为路径开头,和为目标值的路径总数。
int pathSum(TreeNode *root, int sum)
{
if (root == nullptr)
return 0;
int pathImLeading = count(root, sum); // 自己为开头的路径数
int leftPathSum = pathSum(root->left, sum); // 左边路径总数(相信它能算出来)
int rightPathSum =
pathSum(root->right, sum); // 右边路径总数(相信它能算出来)
return leftPathSum + rightPathSum + pathImLeading;
}
int count(TreeNode *node, int sum)
{
if (node == nullptr)
return 0;
// 能不能作为一条单独的路径呢?
int isMe = (node->val == sum) ? 1 : 0;
// 左边的,你那边能凑几个 sum - node.val ?
int leftNode = count(node->left, sum - node->val);
// 右边的,你那边能凑几个 sum - node.val ?
int rightNode = count(node->right, sum - node->val);
return isMe + leftNode + rightNode; // 我这能凑这么多个
}
还是那句话,明白每个函数能做的事,并相信它们能够完成。
总结下,PathSum 函数提供了二叉树遍历框架,在遍历中对每个节点调用 count 函数。count 函数也是一个二叉树遍历,用于寻找以该节点开头的目标值路径。
贪心
引入
贪心算法(英语:greedy algorithm),是用计算机来模拟一个「贪心」的人做出决策的过程。这个人十分贪婪,每一步行动总是按某种指标选取最优的操作。而且他目光短浅,总是只看眼前,并不考虑以后可能造成的影响。
可想而知,并不是所有的时候贪心法都能获得最优解,所以一般使用贪心法的时候,都要确保自己能证明其正确性。
解释
适用范围
贪心算法在有最优子结构的问题中尤为有效。最优子结构的意思是问题能够分解成子问题来解决,子问题的最优解能递推到最终问题的最优解。
证明
贪心算法有两种证明方法:反证法和归纳法。一般情况下,一道题只会用到其中的一种方法来证明。
- 反证法:如果交换方案中任意两个元素/相邻的两个元素后,答案不会变得更好,那么可以推定目前的解已经是最优解了。
- 归纳法:先算得出边界情况(例如 n = 1 n = 1 n=1)的最优解 F 1 F_1 F1,然后再证明:对于每个 n n n, F n + 1 F_{n+1} Fn+1 都可以由 F n F_{n} Fn 推导出结果。
要点
常见题型
在提高组难度以下的题目中,最常见的贪心有两种。
- 「我们将 XXX 按照某某顺序排序,然后按某种顺序(例如从小到大)选择。」。
- 「我们每次都取 XXX 中最大/小的东西,并更新 XXX。」(有时「XXX 中最大/小的东西」可以优化,比如用优先队列维护)
二者的区别在于一种是离线的,先处理后选择;一种是在线的,边处理边选择。
排序解法
用排序法常见的情况是输入一个包含几个(一般一到两个)权值的数组,通过排序然后遍历模拟计算的方法求出最优值。
后悔解法
思路是无论当前的选项是否最优都接受,然后进行比较,如果选择之后不是最优了,则反悔,舍弃掉这个选项;否则,正式接受。如此往复。
区别
与动态规划的区别
贪心算法与动态规划的不同在于它对每个子问题的解决方案都做出选择,不能回退。动态规划则会保存以前的运算结果,并根据以前的结果对当前进行选择,有回退功能。
例题
邻项交换法的例题
恰逢 H 国国庆,国王邀请 n 位大臣来玩一个有奖游戏。首先,他让每个大臣在左、右手上面分别写下一个整数,国王自己也在左、右手上各写一个整数。然后,让这 n 位大臣排成一排,国王站在队伍的最前面。排好队后,所有的大臣都会获得国王奖赏的若干金币,每位大臣获得的金币数分别是:排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数,然后向下取整得到的结果。
国王不希望某一个大臣获得特别多的奖赏,所以他想请你帮他重新安排一下队伍的顺序,使得获得奖赏最多的大臣,所获奖赏尽可能的少。注意,国王的位置始终在队伍的最前面。
解题思路
设排序后第 i i i 个大臣左右手上的数分别为 a i , b i a_i, b_i ai,bi。考虑通过邻项交换法推导贪心策略。
用 s s s 表示第 i i i 个大臣前面所有人的 a i a_i ai 的乘积,那么第 i i i 个大臣得到的奖赏就是 s b i \dfrac{s} {b_i} bis,第 i + 1 i + 1 i+1 个大臣得到的奖赏就是 s ⋅ a i b i + 1 \dfrac{s \cdot a_i} {b_{i+1}} bi+1s⋅ai。
如果我们交换第 i i i 个大臣与第 i + 1 i + 1 i+1 个大臣,那么此时的第 i i i 个大臣得到的奖赏就是 s b i + 1 \dfrac{s} {b_{i+1}} bi+1s,第 i + 1 i + 1 i+1 个大臣得到的奖赏就是 s ⋅ a i + 1 b i \dfrac{s \cdot a_{i+1}} {b_i} bis⋅ai+1。
如果交换前更优当且仅当
max ( s b i , s ⋅ a i b i + 1 ) < max ( s b i + 1 , s ⋅ a i + 1 b i ) \max \left(\dfrac{s} {b_i}, \dfrac{s \cdot a_i} {b_{i+1}}\right) < \max \left(\dfrac{s} {b_{i+1}}, \dfrac{s \cdot a_{i+1}} {b_i}\right) max(bis,bi+1s⋅ai)<max(bi+1s,bis⋅ai+1)
提取出相同的 s s s 并约分得到
max ( 1 b i , a i b i + 1 ) < max ( 1 b i + 1 , a i + 1 b i ) \max \left(\dfrac{1} {b_i}, \dfrac{a_i} {b_{i+1}}\right) < \max \left(\dfrac{1} {b_{i+1}}, \dfrac{a_{i+1}} {b_i}\right) max(bi1,bi+1ai)<max(bi+11,biai+1)
然后分式化成整式得到
max ( b i + 1 , a i ⋅ b i ) < max ( b i , a i + 1 ⋅ b i + 1 ) \max (b_{i+1}, a_i\cdot b_i) < \max (b_i, a_{i+1}\cdot b_{i+1}) max(bi+1,ai⋅bi)<max(bi,ai+1⋅bi+1)
实现的时候我们将输入的两个数用一个结构体来保存并重载运算符:
struct uv
{
int a, b;
bool operator<(const uv &x) const
{
return max(x.b, a * b) < max(b, x.a * x.b);
}
};
然后对这些结构体进行排序,最后按照排序后的顺序输出即可。
后悔法的例题
约翰的工作日从 0 0 0 时刻开始,有 1 0 9 10^9 109 个单位时间。在任一单位时间,他都可以选择编号 1 1 1 到 N N N 的 N ( 1 ≤ N ≤ 1 0 5 ) N(1 \leq N \leq 10^5) N(1≤N≤105) 项工作中的任意一项工作来完成。工作 i i i 的截止时间是 D i ( 1 ≤ D i ≤ 1 0 9 ) D_i(1 \leq D_i \leq 10^9) Di(1≤Di≤109),完成后获利是 P i ( 1 ≤ P i ≤ 1 0 9 ) P_i( 1\leq P_i\leq 10^9 ) Pi(1≤Pi≤109)。在给定的工作利润和截止时间下,求约翰能够获得的利润最大为多少。
解题思路
- 先假设每一项工作都做,将各项工作按截止时间排序后入队;
- 在判断第
i项工作做与不做时,若其截至时间符合条件,则将其与队中报酬最小的元素比较,若第i项工作报酬较高(后悔),则ans += a[i].p - q.top()。
用优先队列(小根堆)来维护队首元素最小。 - 当
a[i].d<=q.size()可以这么理解从0开始到a[i].d这个时间段只能做a[i].d个任务,而若q.size()>=a[i].d说明完成q.size()个任务时间大于等于a[i].d的时间,所以当第i个任务获利比较大的时候应该把最小的任务从优先级队列中换出。
参考代码
#include 复杂度分析
空间复杂度:当输入 n n n 个任务时使用 n n n 个 a a a 数组元素,优先队列中最差情况下会储存 n n n 个元素,则空间复杂度为 O ( n ) O(n) O(n)。
时间复杂度:sort 的时间复杂度为 O ( n log n ) O(n\log n) O(nlogn),维护优先队列的时间复杂度为 O ( n log n ) O(n\log n) O(nlogn),综上所述,时间复杂度为 O ( n log n ) O(n\log n) O(nlogn)。
排序
定义
排序算法(英语:Sorting algorithm)是一种将一组特定的数据按某种顺序进行排列的算法。排序算法多种多样,性质也大多不同。
性质
稳定性
稳定性是指相等的元素经过排序之后相对顺序是否发生了改变。
拥有稳定性这一特性的算法会让原本有相等键值的纪录维持相对次序,即如果一个排序算法是稳定的,当有两个相等键值的纪录 R R R 和 S S S,且在原本的列表中 R R R 出现在 S S S 之前,在排序过的列表中 R R R 也将会是在 S S S 之前。
基数排序、计数排序、插入排序、冒泡排序、归并排序是稳定排序。
选择排序、堆排序、快速排序、希尔排序不是稳定排序。
时间复杂度
时间复杂度用来衡量一个算法的运行时间和输入规模的关系,通常用 O O O 表示。
简单计算复杂度的方法一般是统计「简单操作」的执行次数,有时候也可以直接数循环的层数来近似估计。
时间复杂度分为最优时间复杂度、平均时间复杂度和最坏时间复杂度。程序设计竞赛中要考虑的一般是最坏时间复杂度,因为它代表的是算法运行水平的下界,在评测中不会出现更差的结果了。
基于比较的排序算法的时间复杂度下限是 O ( n log n ) O(n\log n) O(nlogn) 的。
当然也有不是 O ( n log n ) O(n\log n) O(nlogn) 的。例如,计数排序 的时间复杂度是 O ( n + w ) O(n+w) O(n+w),其中 w w w 代表输入数据的值域大小。
以下是几种排序算法的比较。
空间复杂度
与时间复杂度类似,空间复杂度用来描述算法空间消耗的规模。一般来说,空间复杂度越小,算法越好。
常见排序算法对比
| 排序算法 | 最好时间复杂度 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 | 排序方式 |
|---|---|---|---|---|---|---|
| 冒泡排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 | 比较 |
| 选择排序 | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 不稳定 | 比较 |
| 插入排序 | O ( n ) O(n) O(n) | O ( n 2 ) O(n^2) O(n2) | O ( n 2 ) O(n^2) O(n2) | O ( 1 ) O(1) O(1) | 稳定 | 比较 |
| 希尔排序 | O ( n ) O(n) O(n) | O ( n log 2 n ) O(n\log^2 n) O(nlog2n) | O ( n log 2 n ) O(n\log^2 n) O(nlog2n) | O ( 1 ) O(1) O(1) | 不稳定 | 比较 |
| 归并排序 | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | O ( n ) O(n) O(n) | 稳定 | 比较 |
| 快速排序 | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | O ( n 2 ) O(n^2) O(n2) | O ( log n ) O(\log n) O(logn) | 不稳定 | 比较 |
| 堆排序 | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | O ( n log n ) O(n\log n) O(nlogn) | O ( 1 ) O(1) O(1) | 不稳定 | 比较 |
| 计数排序 | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( k ) O(k) O(k) | 稳定 | 非比较 |
| 桶排序 | O ( n + k ) O(n+k) O(n+k) | O ( n + k ) O(n+k) O(n+k) | O ( n 2 ) O(n^2) O(n2) | O ( n + k ) O(n+k) O(n+k) | 稳定 | 非比较 |
| 基数排序 | O ( n k ) O(nk) O(nk) | O ( n k ) O(nk) O(nk) | O ( n k ) O(nk) O(nk) | O ( n + k ) O(n+k) O(n+k) | 稳定 | 非比较 |
- 平方阶( O ( n 2 ) O(n^2) O(n2))排序
各类简单排序,冒泡、选择、插入 - 线性对数阶( O ( n log n ) O(n\log n) O(nlogn))排序
快速排序、归并排序、堆排序 - O ( n 1 + § ) O(n^{1+\S}) O(n1+§) 排序, § \S § 是介于 0 0 0 到 1 1 1 之间的常数
希尔排序 - 线性阶( O ( n ) O(n) O(n))排序
基数排序、计数排序、桶排序
STL 中的排序
C++ STL 中最常用的排序函数是 sort。
旧版 C++ 标准中仅要求它的 平均 时间复杂度达到 O ( n log n ) O(n\log n) O(nlogn)。C++11 标准以及后续标准要求它的 最坏 时间复杂度达到 O ( n log n ) O(n\log n) O(nlogn)。
C++ 标准并未严格要求此函数的实现算法,具体实现取决于编译器。libstdc++ 中的实现使用了内省排序。
内省排序
定义
内省排序(英语:Introsort 或 Introspective sort)是快速排序和堆排序的结合,由 David Musser 于 1997 年发明。内省排序其实是对快速排序的一种优化,保证了最差时间复杂度为 O ( n log n ) O(n\log n) O(nlogn)。
性质
内省排序将快速排序的最大递归深度限制为 ⌊ log 2 n ⌋ \lfloor \log_2n \rfloor ⌊log2n⌋,超过限制时就转换为堆排序。这样既保留了快速排序内存访问的局部性,又可以防止快速排序在某些情况下性能退化为 O ( n 2 ) O(n^2) O(n2)。
实现
从 2000 年 6 月起,SGI C++ STL 的 stl_algo.h 中 sort() 函数的实现采用了内省排序算法。
应用
理解数据的特点
使用排序处理数据有利于理解数据的特点,方便我们之后的分析与视觉化。像一些生活中的例子比如词典,菜单,如果不是按照一定顺序排列的话,人们想要找到自己需要的东西的时间就会大大增加。
计算机需要处理大规模的数据,排序后,人们可以根据数据的特点和需求来设计计算机的后续处理流程。
降低时间复杂度
使用排序预处理可以降低求解问题所需要的时间复杂度,通常是一个以空间换取时间的平衡。如果一个排序好的列表需要被多次分析的话,只需要耗费一次排序所需要的资源是很划算的,因为之后的每次分析都可以减少很多时间。
示例:检查给定数列中是否有相等的元素
考虑一个数列,你需要检查其中是否有元素相等。
一个朴素的做法是检查每一个数对,并判断这一对数是否相等。时间复杂度是 O ( n 2 ) O(n^2) O(n2)。
我们不妨先对这一列数排序,之后不难发现:如果有相等的两个数,它们一定在新数列中处于相邻的位置上。这时,只需要 O ( n ) O(n) O(n) 地扫一遍新数列了。
总的时间复杂度是排序的复杂度 O ( n log n ) O(n\log n) O(nlogn)。
作为查找的预处理
排序是 二分查找 所要做的预处理工作。在排序后使用二分查找,可以以 O ( log n ) O(\log n) O(logn) 的时间在序列中查找指定的元素。
前缀和 & 差分
前缀和
定义
前缀和可以简单理解为「数列的前 n n n 项的和」,是一种重要的预处理方式,能大大降低查询的时间复杂度。
C++ 标准库中实现了前缀和函数 std::partial_sum,定义于头文件
例题
题目描述
有 N N N 个的正整数放到数组 A A A 里,现在要求一个新的数组 B B B,新数组的第 i i i 个数 B [ i ] B[i] B[i] 是原数组 A A A 第 0 0 0 到第 i i i 个数的和。
输入:
5
1 2 3 4 5
输出:
1 3 6 10 15
解题思路
递推:B[0] = A[0],对于 i ≥ 1 i \ge 1 i≥1 则 B[i] = B[i-1] + A[i]。
参考代码
#include 二维/多维前缀和
多维前缀和的普通求解方法几乎都是基于容斥原理。
示例:一维前缀和扩展到二维前缀和
比如我们有这样一个矩阵 a a a,可以视为二维数组:
1 2 4 3
5 1 2 4
6 3 5 9
我们定义一个矩阵 sum \textit{sum} sum 使得 sum x , y = ∑ i = 1 x ∑ j = 1 y a i , j \textit{sum}_{x,y} = \sum\limits_{i=1}^x \sum\limits_{j=1}^y a_{i,j} sumx,y=i=1∑xj=1∑yai,j,那么这个矩阵长这样:
1 3 7 10
6 9 15 22
12 18 29 45
第一个问题就是递推求 sum \textit{sum} sum 的过程, sum i , j = sum i − 1 , j + sum i , j − 1 − sum i − 1 , j − 1 + a i , j \textit{sum}_{i,j} = \textit{sum}_{i - 1,j} + \textit{sum}_{i,j - 1} - \textit{sum}_{i - 1,j - 1} + a_{i,j} sumi,j=sumi−1,j+sumi,j−1−sumi−1,j−1+ai,j。
因为同时加了 sum i − 1 , j 和 sum i , j − 1 \textit{sum}_{i - 1,j} 和 \textit{sum}_{i,j - 1} sumi−1,j和sumi,j−1,故重复了 sum i − 1 , j − 1 \textit{sum}_{i - 1,j - 1} sumi−1,j−1,减去。
第二个问题就是如何应用,譬如求 ( x 1 , y 1 ) − ( x 2 , y 2 ) (x_1,y_1) - (x_2,y_2) (x1,y1)−(x2,y2) 子矩阵的和。
那么,根据类似的思考过程,易得答案为 sum x 2 , y 2 − sum x 1 − 1 , y 2 − s u m x 2 , y 1 − 1 + s u m x 1 − 1 , y 1 − 1 \textit{sum}_{x_2,y_2} - \textit{sum}_{x_1 - 1,y_2} - sum_{x_2,y_1 - 1} + sum_{x_1 - 1,y_1 - 1} sumx2,y2−sumx1−1,y2−sumx2,y1−1+sumx1−1,y1−1。
例题
在一个 n × m n\times m n×m 的只包含 0 0 0 和 1 1 1 的矩阵里找出一个不包含 0 0 0 的最大正方形,输出边长。
参考代码
#include 其他
除了一维和二维前缀和以外,还有更高维的前缀和以及树上前缀和,这里不再赘述。
差分
解释
差分是一种和前缀和相对的策略,可以当做是求和的逆运算。
这种策略的定义是令 b i = { a i − a i − 1 i ∈ [ 2 , n ] a 1 i = 1 b_i=\begin{cases}a_i-a_{i-1}\,&i \in[2,n] \\ a_1\,&i=1\end{cases} bi={ai−ai−1a1i∈[2,n]i=1
性质
- a i a_i ai 的值是 b i b_i bi 的前缀和,即 a n = ∑ i = 1 n b i a_n=\sum\limits_{i=1}^nb_i an=i=1∑nbi
- 计算 a_i 的前缀和 s u m = ∑ i = 1 n a i = ∑ i = 1 n ∑ j = 1 i b j = ∑ i n ( n − i + 1 ) b i sum=\sum\limits_{i=1}^na_i=\sum\limits_{i=1}^n\sum\limits_{j=1}^{i}b_j=\sum\limits_{i}^n(n-i+1)b_i sum=i=1∑nai=i=1∑nj=1∑ibj=i∑n(n−i+1)bi
它可以维护多次对序列的一个区间加上一个数,并在最后询问某一位的数或是多次询问某一位的数。注意修改操作一定要在查询操作之前。
譬如使数组 a a a [ l , r ] [l,r] [l,r] 中的每个数加上一个 k k k,即
b l ← b l + k , b r + 1 ← b r + 1 − k b_l \leftarrow b_l + k,b_{r + 1} \leftarrow b_{r + 1} - k bl←bl+k,br+1←br+1−k
其中 b l + k = a l + k − a l − 1 , b r + 1 − k = a r + 1 − ( a r + k ) b_l+k=a_l+k-a_{l-1},b_{r+1}-k=a_{r+1}-(a_r+k) bl+k=al+k−al−1,br+1−k=ar+1−(ar+k) 最后做一遍前缀和就好了。
C++ 标准库中实现了差分函数 std::adjacent_difference,定义于头文件
二分
本章将简要介绍二分查找,由二分法衍生的三分法以及二分答案。
二分法
定义
二分查找(英语:binary search),也称折半搜索(英语:half-interval search)、对数搜索(英语:logarithmic search),是用来在一个有序数组中查找某一元素的算法。
过程
以在一个升序数组中查找一个数为例。
它每次考察数组当前部分的中间元素,如果中间元素刚好是要找的,就结束搜索过程;如果中间元素小于所查找的值,那么左侧的只会更小,不会有所查找的元素,只需到右侧查找;如果中间元素大于所查找的值同理,只需到左侧查找。
性质
时间复杂度
二分查找的最优时间复杂度为 O ( 1 ) O(1) O(1)。
二分查找的平均时间复杂度和最坏时间复杂度均为 O ( log n ) O(\log n) O(logn)。因为在二分搜索过程中,算法每次都把查询的区间减半,所以对于一个长度为 n n n 的数组,至多会进行 O ( log n ) O(\log n) O(logn) 次查找。
空间复杂度
迭代版本的二分查找的空间复杂度为 O ( 1 ) O(1) O(1)。
递归(无尾调用消除)版本的二分查找的空间复杂度为 O ( log n ) O(\log n) O(logn)。
实现
int binary_search(int start, int end, int key)
{
int ret = -1; // 未搜索到数据返回-1下标
int mid;
while (start <= end)
{
mid = start + ((end - start) >> 1); // 防止溢出
if (arr[mid] < key)
start = mid + 1;
else if (arr[mid] > key)
end = mid - 1;
else
{
ret = mid;
break;
}
}
return ret;
}
最大值最小化
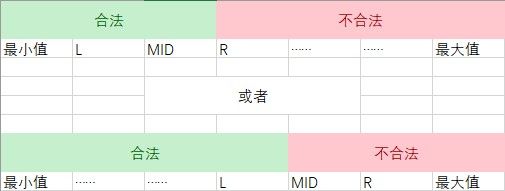
注意,这里的有序是广义的有序,如果一个数组中的左侧或者右侧都满足某一种条件,而另一侧都不满足这种条件,也可以看作是一种有序(如果把满足条件看做 1 1 1,不满足看做 0 0 0,至少对于这个条件的这一维度是有序的)。换言之,二分搜索法可以用来查找满足某种条件的最大(最小)的值。
要求满足某种条件的最大值的最小可能情况(最大值最小化),首先的想法是从小到大枚举这个作为答案的「最大值」,然后去判断是否合法。若答案单调,就可以使用二分搜索法来更快地找到答案。因此,要想使用二分搜索法来解这种「最大值最小化」的题目,需要满足以下三个条件:
- 答案在一个固定区间内;
- 可能查找一个符合条件的值不是很容易,但是要求能比较容易地判断某个值是否是符合条件的;
- 可行解对于区间满足一定的单调性。换言之,如果 x x x 是符合条件的,那么有 x + 1 x + 1 x+1 或者 x − 1 x - 1 x−1 也符合条件。(这样下来就满足了上面提到的单调性)
当然,最小值最大化是同理的。
STL 的二分查找
C++ 标准库中实现了查找首个不小于给定值的元素的函数 std::lower_bound 和查找首个大于给定值的元素的函数 std::upper_bound,二者均定义于头文件
二者均采用二分实现,所以调用前必须保证元素有序。
二分答案
解题的时候往往会考虑枚举答案然后检验枚举的值是否正确。若满足单调性,则满足使用二分法的条件。把这里的枚举换成二分,就变成了「二分答案」。
例题描述
伐木工人米尔科需要砍倒 M M M 米长的木材。这是一个对米尔科来说很容易的工作,因为他有一个漂亮的新伐木机,可以像野火一样砍倒森林。不过,米尔科只被允许砍倒单行树木。
米尔科的伐木机工作过程如下:米尔科设置一个高度参数 H H H(米),伐木机升起一个巨大的锯片到高度 H H H,并锯掉所有的树比 H H H 高的部分(当然,树木不高于 H H H 米的部分保持不变)。米尔科就得到树木被锯下的部分。
例如,如果一行树的高度分别为 20 , 15 , 10 , 17 20,~15,~10,~17 20, 15, 10, 17,米尔科把锯片升到 15 15 15 米的高度,切割后树木剩下的高度将是 15 , 15 , 10 , 15 15,~15,~10,~15 15, 15, 10, 15,而米尔科将从第 1 1 1 棵树得到 5 5 5 米木材,从第 4 4 4 棵树得到 2 2 2 米木材,共 7 7 7 米木材。
米尔科非常关注生态保护,所以他不会砍掉过多的木材。这正是他尽可能高地设定伐木机锯片的原因。你的任务是帮助米尔科找到伐木机锯片的最大的整数高度 H H H,使得他能得到木材至少为 M M M 米。即,如果再升高 1 1 1 米锯片,则他将得不到 M M M 米木材。
解题思路
我们可以在 1 1 1 到 1 0 9 10^9 109 中枚举答案,但是这种朴素写法肯定拿不到满分,因为从 1 1 1 枚举到 1 0 9 10^9 109 太耗时间。我们可以在 [ 1 , 1 0 9 ] [1,~10^9] [1, 109] 的区间上进行二分作为答案,然后检查各个答案的可行性(一般使用贪心法)。这就是二分答案。
参考代码
#include 看完了上面的代码,你肯定会有两个疑问:
三分法
引入
如果需要求出单峰函数的极值点,通常使用二分法衍生出的三分法求单峰函数的极值点。
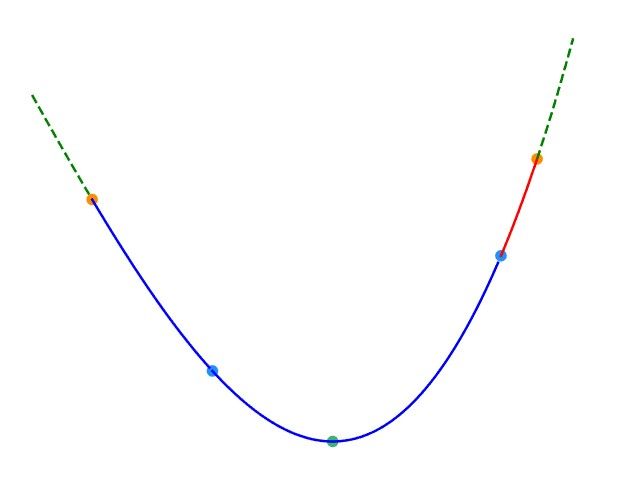
三分法与二分法的基本思想类似,但每次操作需在当前区间 [ l , r ] [l,r] [l,r](下图中除去虚线范围内的部分)内任取两点 l m i d , r m i d ( l m i d < r m i d ) lmid,rmid(lmid < rmid) lmid,rmid(lmid<rmid)(下图中的两蓝点)。如下图,如果 f ( l m i d ) < f ( r m i d ) f(lmid)
三分法每次操作会舍去两侧区间中的其中一个。为减少三分法的操作次数,应使两侧区间尽可能大。因此,每一次操作时的 l m i d lmid lmid 和 r m i d rmid rmid 分别取 m i d − ε mid-\varepsilon mid−ε 和 m i d + ε mid+\varepsilon mid+ε 是一个不错的选择。
实现
在实际使用中, ε \varepsilon ε 的取值一般为 1 0 − 6 ∼ − 8 10^{-6\sim-8} 10−6∼−8,因此在舍弃区间时,我们使用 m i d mid mid 来近似替代 l m i d lmid lmid 或 r m i d rmid rmid。
伪代码
1 Input. A range [ l , r ] meaning that the domain of f ( x ) . 2 Output. The maximum value of f ( x ) and the value of x at that time . 3 Method. 4 while r − l > ε 5 m i d ← l m i d + r m i d 2 6 l m i d ← m i d − ε 7 r m i d ← m i d + ε 8 if f ( l m i d ) < f ( r m i d ) 9 r ← m i d 10 else 11 l ← m i d \begin{array}{ll} 1 & \textbf{Input. } \text{A range } [l,r] \text{ meaning that the domain of } f(x) \text{.} \\ 2 & \textbf{Output. } \text{The maximum value of } f(x) \text{ and the value of } x \text{ at that time } \text{.} \\ 3 & \textbf{Method. } \\ 4 & \textbf{while } r - l > \varepsilon\\ 5 & \qquad mid\gets \frac{lmid+rmid}{2}\\ 6 & \qquad lmid\gets mid - \varepsilon \\ 7 & \qquad rmid\gets mid + \varepsilon \\ 8 & \qquad \textbf{if } f(lmid) < f(rmid) \\ 9 & \qquad \qquad r\gets mid \\ 10 & \qquad \textbf{else } \\ 11 & \qquad \qquad l\gets mid \end{array} 1234567891011Input. A range [l,r] meaning that the domain of f(x).Output. The maximum value of f(x) and the value of x at that time .Method. while r−l>εmid←2lmid+rmidlmid←mid−εrmid←mid+εif f(lmid)<f(rmid)r←midelse l←mid
C++
while (r - l > eps) {
mid = (lmid + rmid) / 2;
lmid = mid - eps;
rmid = mid + eps;
if (f(lmid) < f(rmid))
r = mid;
else
l = mid;
}
例题
题目描述
给定一个 N N N 次函数和范围 [ l , r ] [l, r] [l,r],求出使函数在 [ l , x ] [l, x] [l,x] 上单调递增且在 [ x , r ] [x, r] [x,r] 上单调递减的唯一的 x x x 的值。
解题思路
本题要求求 N N N 次函数在 [ l , r ] [l, r] [l,r] 取最大值时自变量的值,显然可以使用三分法。
参考代码
#include 倍增
定义
倍增法(英语:binary lifting),顾名思义就是翻倍。它能够使线性的处理转化为对数级的处理,大大地优化时间复杂度。
这个方法在很多算法中均有应用,其中最常用的是 RMQ 问题(区间最大/小值问题)和求 LCA(最近公共祖先)。
应用
RMQ 问题
RMQ 是 Range Maximum/Minimum Query 的缩写,表示区间最大(最小)值。
使用倍增思想解决 RMQ 问题的方法是 ST 表。
树上倍增求 LCA
最近公共祖先简称 LCA(Lowest Common Ancestor)。两个节点的最近公共祖先,就是这两个点的公共祖先里面,离根最远的那个。 为了方便,我们记某点集 S = { v 1 , v 2 , … , v n } S=\{v_1,v_2,\ldots,v_n\} S={v1,v2,…,vn} 的最近公共祖先为 LCA ( v 1 , v 2 , … , v n ) \text{LCA}(v_1,v_2,\ldots,v_n) LCA(v1,v2,…,vn) 或 LCA ( S ) \text{LCA}(S) LCA(S)。
LCA 问题可以使用倍增算法求解,也可以通过欧拉序转化为等规模的 RMQ 问题求解。
例题
题目描述
如何用尽可能少的砝码称量出 [ 0 , 31 ] [0,31] [0,31] 之间的所有重量?(只能在天平的一端放砝码)
解题思路
答案是使用 1 2 4 8 16 这五个砝码,可以称量出 [ 0 , 31 ] [0,31] [0,31] 之间的所有重量。同样,如果要称量 [ 0 , 127 ] [0,127] [0,127] 之间的所有重量,可以使用 1 2 4 8 16 32 64 这七个砝码。每次我们都选择 2 的整次幂作砝码的重量,就可以使用极少的砝码个数量出任意我们所需要的重量。
为什么说是极少呢?因为如果我们要量出 [ 0 , 1023 ] [0,1023] [0,1023] 之间的所有重量,只需要 10 个砝码,需要量出 [ 0 , 1048575 ] [0,1048575] [0,1048575] 之间的所有重量,只需要 20 个。如果我们的目标重量翻倍,砝码个数只需要增加 1。这叫「对数级」的增长速度,因为砝码的所需个数与目标重量的范围的对数成正比。
构造
引入
构造题是比赛中常见的一类题型。
从形式上来看,问题的答案往往具有某种规律性,使得在问题规模迅速增大的时候,仍然有机会比较容易地得到答案。
这要求解题时要思考问题规模增长对答案的影响,这种影响是否可以推广。例如,在设计动态规划方法的时候,要考虑从一个状态到后继状态的转移会造成什么影响。
特点
构造题一个很显著的特点就是高自由度,也就是说一道题的构造方式可能有很多种,但是会有一种较为简单的构造方式满足题意。看起来是放宽了要求,让题目变的简单了,但很多时候,正是这种高自由度导致题目没有明确思路而无从下手。
构造题另一个特点就是形式灵活,变化多样。并不存在一个通用解法或套路可以解决所有构造题,甚至很难找出解题思路的共性。
例题1
题目描述
codeforces Round #384 (Div. 2) C.Vladik and fractions
构造一组 x , y , z x,y,z x,y,z,使得对于给定的 n n n,满足 1 x + 1 y + 1 z = 2 n \dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=\dfrac{2}{n} x1+y1+z1=n2
样例1
输入:
3
输出:
2 7 42
样例2
输入:
7
输出:
7 8 56
解题思路
从样例二可以看出本题的构造方法。
显然 n , n + 1 , n ( n + 1 ) n,n+1,n(n+1) n,n+1,n(n+1) 为一组合法解。特殊地,当 n = 1 n=1 n=1 时,无解,这是因为 n + 1 n+1 n+1 与 n ( n + 1 ) n(n+1) n(n+1) 此时相等。
至于构造思路是怎么产生的,大概就是观察样例加上一点点数感了吧。此题对于数学直觉较强的人来说并不难。
例题2
题目描述
Luogu P3599 Koishi Loves Construction
Task1:试判断能否构造并构造一个长度为 n n n 的 1 … n 1\dots n 1…n 的排列,满足其 n n n 个前缀和在模 n n n 的意义下互不相同
Task2:试判断能否构造并构造一个长度为 n n n 的 1 … n 1\dots n 1…n 的排列,满足其 n n n 个前缀积在模 n n n 的意义下互不相同
解题思路
对于 task1:
当 n n n 为奇数时,无法构造出合法解;
当 n n n 为偶数时,可以构造一个形如 n , 1 , n − 2 , 3 , ⋯ n,1,n-2,3,\cdots n,1,n−2,3,⋯ 这样的数列。
首先,我们可以发现 n n n 必定出现在数列的第一位,否则 n n n 出现前后的两个前缀和必然会陷入模意义下相等的尴尬境地;
然后,我们考虑构造出整个序列的方式:
考虑通过构造前缀和序列的方式来获得原数列,可以发现前缀和序列两两之间的差在模意义下不能相等,因为前缀和序列的差分序列对应着原来的排列。
因此我们尝试以前缀和数列在模意义下为
0 , 1 , − 1 , 2 , − 2 , ⋯ 0,1,-1,2,-2,\cdots 0,1,−1,2,−2,⋯
这样的形式来构造这个序列,不难发现它完美地满足所有限制条件。
对于 task2:
当 n n n 为除 4 4 4 以外的合数时,无法构造出合法解
当 n n n 为质数或 4 4 4 时,可以构造一个形如 1 , 2 1 , 3 2 , ⋯ , n − 1 n − 2 , n 1,\dfrac{2}{1},\dfrac{3}{2},\cdots,\dfrac{n-1}{n-2},n 1,12,23,⋯,n−2n−1,n 这样的数列
先考虑什么时候有解:
显然,当 n n n 为合数时无解。因为对于一个合数来说,存在两个比它小的数 p , q p,q p,q 使得 p × q ≡ 0 ( m o d n ) p\times q \equiv 0 \pmod n p×q≡0(modn),如 ( 3 × 6 ) % 9 = 0 (3\times6)\%9=0 (3×6)%9=0。那么,当 p , q p,q p,q 均出现过后,数列的前缀积将一直为 0 0 0,故合数时无解。特殊地,我们可以发现 4 = 2 × 2 4=2\times 2 4=2×2,无满足条件的 p , q p,q p,q,因此存在合法解。
我们考虑如何构造这个数列:
和 task1 同样的思路,我们发现 1 1 1 必定出现在数列的第一位,否则 1 1 1 出现前后的两个前缀积必然相等;而 n n n 必定出现在数列的最后一位,因为 n n n 出现位置后的所有前缀积在模意义下都为 0 0 0。看完几组样例以后发现,所有样例中均有一组合法解满足前缀积在模意义下为 1 , 2 , 3 , ⋯ , n 1,2,3,\cdots,n 1,2,3,⋯,n,因此我们可以构造出上文所述的数列来满足这个条件。那么我们只需证明这 n n n 个数互不相同即可。
我们发现这些数均为 1 ⋯ n − 2 1 \cdots n-2 1⋯n−2 的逆元 + 1 +1 +1,因此各不相同,此题得解。