迷宫问题的所有路径，递归解法，不用栈，极精简56行，c/c++描述

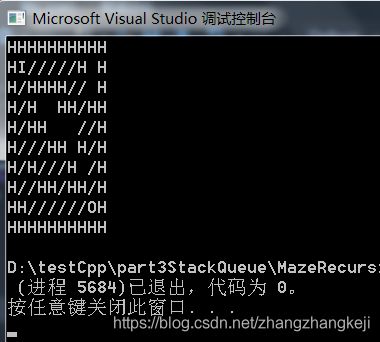
  如图的一个迷宫，是一个10 X 10的矩阵，以 H 表示墙壁障碍物，以空格表示可以走的路径。起点是坐标（1，1），字符 ‘I’,表示in，终点是坐标（8，8），以字符‘O’表示，out。总共有几条路径可以从起点到终点呢？，而且，我们必然可以从所有路径中找到最短路径。

  测试结果如下，同咱们的肉眼观察，只有三条路径。

  全部代码如下，只有这一个源文件，极为精简。充分应用了递归。充分发挥编译器提供的递归功能。

#include
using namespace std;
#define MAXSIZE 100
struct Step {
	int row;
	int column;
};
char maze[10][10] = {
	'H','H','H','H','H','H','H','H','H','H',
	'H',' ',' ',' ',' ',' ',' ','H',' ','H',
	'H',' ','H','H','H','H',' ',' ',' ','H',
	'H',' ','H',' ',' ','H','H',' ','H','H',
	'H',' ','H','H',' ',' ',' ',' ',' ','H',
	'H',' ',' ',' ','H','H',' ','H',' ','H',
	'H',' ','H',' ',' ',' ','H',' ',' ','H',
	'H',' ',' ','H','H',' ','H','H',' ','H',
	'H','H',' ',' ',' ',' ',' ',' ',' ','H',
	'H','H','H','H','H','H','H','H','H','H'
};
void findAllPath(Step steps[MAXSIZE], int lastStep,
	int inRow, int inColumn, int& outRow, int& outColumn) {
	if (maze[inRow][inColumn] == 'H')
		return;
	for (int i = 0; i <= lastStep; i++)
		if (inRow == steps[i].row && inColumn == steps[i].column)
			return;
	lastStep++;
	steps[lastStep].row = inRow;
	steps[lastStep].column = inColumn;
	if (inRow == outRow && inColumn == outColumn) {
		for (int i = 0; i <= lastStep; i++)
			maze[steps[i].row][steps[i].column] = '/';
		return;
	}

	findAllPath(steps, lastStep, inRow, inColumn + 1, outRow, outColumn);//right
	findAllPath(steps, lastStep, inRow + 1, inColumn, outRow, outColumn);//down
	findAllPath(steps, lastStep, inRow, inColumn - 1, outRow, outColumn);//left
	findAllPath(steps, lastStep, inRow - 1, inColumn, outRow, outColumn);//up
}
void printAllPath() {
	maze[1][1] = 'I';
	maze[8][8] = 'O';
	for (int row = 0; row <= 9; row++) {
		for (int column = 0; column <= 9; column++)
			cout << maze[row][column];
		cout << endl;
	}
}
int main() {
	Step steps[MAXSIZE];
	int inRow = 1, inColumn = 1, outRow = 8, outColumn = 8;
	findAllPath(steps,-1,inRow,inColumn,outRow,outColumn);
	printAllPath();
	return 0;
}

  整个程序包括一个核心的查找路径的函数findAllPath，一个输出矩阵数组的函数printAllPath，再就是主函数main。或许大家直接看代码就懂了。但我还要再逼逼几句。说下程序查找思路。从起点开始，沿上下左右任意方向，只要能到达终点，就是找到了一个完整的路径。如何用递归的方法查找出所有的路径呢？
  递归查找思路是，从起点空格查找到新的空格，并以新的空格为起点，再次调用查找函数，同时把已经走过的路径保存在一个数组里，当起点坐标等于终点坐标时，表示找到了一个完整路径，而此时数组里就存储了对应路径的完整信息，即经过的每一步的字符的坐标。
  用栈的方法，我们同样可以找到一条或者是所有路径。栈里保存了路径中的每一步信息，即每个空格的坐标。找到一条路径后，从终点开始退栈，相当于原路返回，同时核对路径走过的每一个空格，是否有剩余的方向也是对应着空格，若是，则把相邻的这个空格入栈，作为新路径的一部分，继续往终点方向查找，若原路径中的空格没有剩余合适的方向，即剩余的方向全是墙壁H或者是本路径里走过的前一个空格，则继续退栈。直至退栈到起点，当起点也没有剩余方向是可以走的空格时，表示已经查询完了所有路径，程序结束。
  递归思路中，可以不用栈，但也要用一个数组存储路径中走过的每一个步的坐标（非墙壁H，即为空格，或者是上一条路径中走过的‘/’也可以，路径只要不完全重合，就是新路径）。同时设置一个变量int lastStep存储数组中最后一步的数组下标。因为c/c++不允许使用变长数组，只能使用足够长的定长数组。但数组里存储了几步了呢？所有咱们用lastStep存储数组里最后一个步的下标。步是一个结构体变量，存储每一个字符的行列坐标。当最后一步是终点时，就表示找到了一条路径。并把路径里的空格全部改为斜杠‘/’。以便最后在屏幕上显示。
  从数组里最后一步，查找下一个步时，有上下左右四个方向，遇到的是墙壁H，则墙壁H不能入数组，遇到的空格或者‘/’是路径数组里已有的，也不能再入数组，否则就会形成死循环。定下这条规则后，新入数组的路径必能一步步接近终点。
  那么找到一条路径后如何像栈的回溯一样继续查找新的路径呢？栈是进行了退栈，可是我们用数组怎么做呢？如何让lastStep伴随着路径返回同步减少呢，始终指向数组里最后一个步？从终点开始返回继续查找新路径，或者说伴随着递归结束，返回被调函数，如何让lastStep自动也减少呢？
  这里我们巧妙运用了程序顺序执行时只会从上到下执行编译的规则，保证了从右下左上四个方向（右和下为优先探测方向）探测新路径时的不重不漏。也利用了递归调用属于函数调用，参数进行值传递时，被调函数的实参值不会因调用而发生改变的规则。设置lastStep为值传递，这样递归调用结束回到被调函数后，被调函数的lastStep始终没有发生改变，始终指向被调函数里路径数组里的最后一步。
  数组里到底存储了多少数据不重要。我们要保证的是程序执行到本递归函数时，数组里存储的已经走过的路径是准确的，和正在执行本查找函数保持对应。以便于本函数探测完数组里最后一步的右下左上所有方向。lastStep值采用值传递，恰好可以满足递归调用时的数据同步需求，本函数从形参数组里接收的已走过路径和已走过路径最后一步的数组下标lastStep始终保持对应。
谢谢阅读。