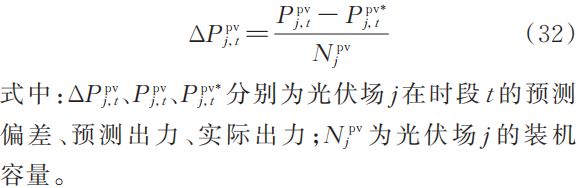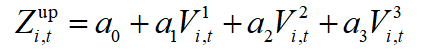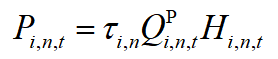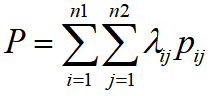(文章复现)梯级水光互补系统最大化可消纳电量期望短期优化调度模型matlab代码

参考文献：

[1]罗彬,陈永灿,刘昭伟等.梯级水光互补系统最大化可消纳电量期望短期优化调度模型[J].电力系统自动化,2023,47(10):66-75.

1.基本原理

1.1 目标函数

        考虑光伏出力的不确定性，以梯级水光互补系统的可消纳电量期望最大为目标，函数可表示为：

1.2约束条件

1.2.1 电站约束

1）水量平衡约束

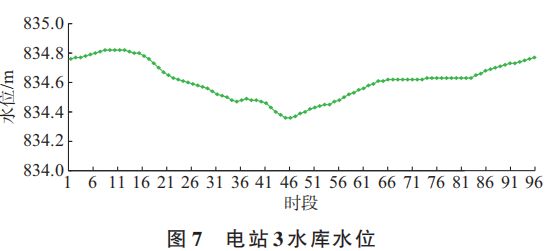
2）水库水位约束

 3）初始水位和末水位控制

4）出库流量约束

5）电站出力约束

6）水位-库容关系

7）尾水位-泄流量关系

1.2.2 机组约束

1）机组出力约束

2）机组发电流量约束

3）机组振动区约束

4）机组开、停机持续时间约束

 

机组在调度期内的最大开机次数，以避免频繁开停机。

5）机组出力爬坡约束

6）机组出力波动限制约束

7）机组发电水头约束

8）水头损失函数

9）机组动力特性关系

1.2.3 电网约束

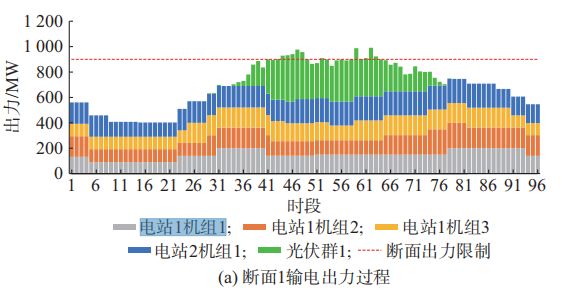
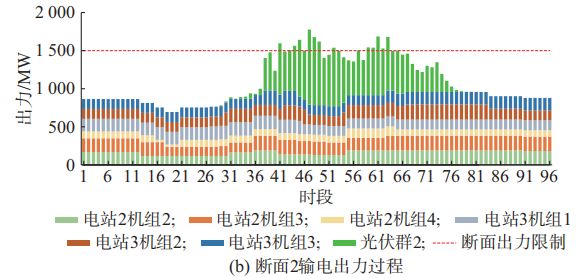
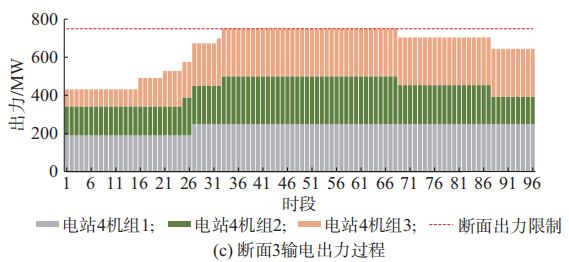
1）梯级水电出力范围约束

2）分区断面约束

从目标函数和分区断面约束可以看出，弃电量中未设置弃水、弃光的优先级，模型目标会使得梯级水电在允许出力范围内优先蓄水减发，以提升受阻断面内光伏消纳量，从而提升互补系统整体可消纳水平，但为保障电网供电支撑无法继续减发时，受到分区断面限制而造成弃光也不可避免。

2.模型求解

2.1 模型转换

        MILP模型构建的关键在于模型的线性化转换 ，所提模型非线性约束包括式（10）、式（11）、式（16）、式（19）、式（21）和式（22）。其中，水位-库容、尾水位-泄流量以及水头损失函数可采用分段线性的方式进行处理［22］。 机组的动力特性参考文献［26］，采用三角形权值技术进行处理。特殊地，对于季调节及以上电站，日内始末水位变化幅度较小，可在初始水位附近采用线性函数表示水位库容关系。

        1）机组振动区约束线性化

        大型机组可能存在多个振动区，将出力在最大最小出力范围内划分为多个非连续的安全运行区间。借鉴文献［21］，文中假设机组振动区不随机组水头变化而改变，即固定的振动区，假设机组有 K 个振动区，则有 K + 1 个安全运行区间，即

        2）水电机组出力波动限制约束线性化

        水电机组出力的频繁波动表现为相邻时段出力的向上或向下调节。区别于已有文献中采用的关联搜索［27］ 和负荷重构［28］ 等方法，文中创新性地通过引入调节指标变量进行处理，可有效提高求解效率。

 

        因此 ，式（19）的非线性约束可用式（29）—式（31）替代。如图1所示机组状态变化示意图，当机组稳定出力时间达到 te 后，机组具有上调、下调和平稳出力 3 种有效状态，假设此时为 t0 时刻，若 t1 时刻上调或下调出力，调整之后则仅有平稳出力状态有效，上调和下调的状态暂时无效，直到稳定出力时间再次达到 te 后，机组上调和下调的状态重新有效，如此逐时段约束保证机组出力的稳定性。 

 

2.2 光伏出力场景构建

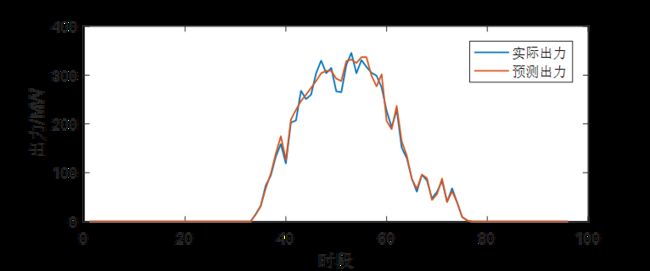
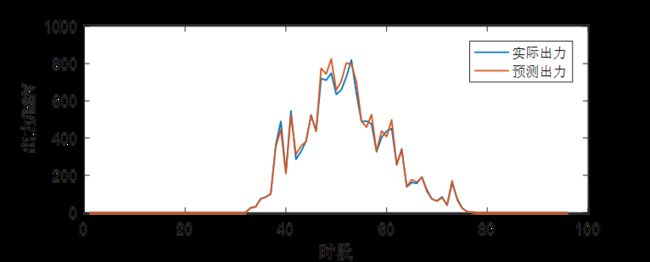
        受天气变化、预测方法等因素影响，光伏预测出力与实际出力之间的偏差客观存在。文中以历史偏差数据为样本，采用模糊聚类分析，构建光伏出力场景，具体方法流程如下。

        1）出力偏差处理

        2）模糊聚类分析

        以光伏场站历史日内96 点预测出力与实际出力偏差曲线为样本，进行模糊聚类分析，并采用聚类综合质量确定最佳聚类数，最后以各类别的模糊聚类中心构建预测出力偏差场景，具体公式和详细步骤可参考文献［29］。

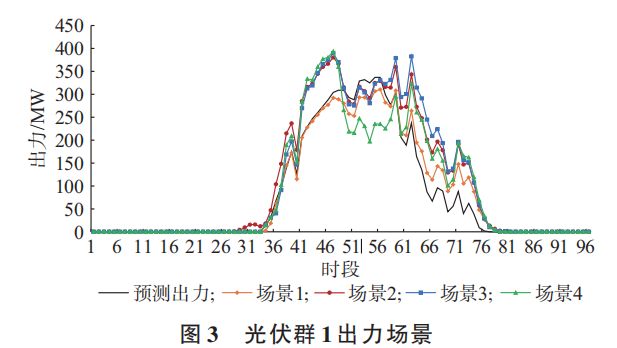
        3）光伏出力场景

2.3 求解流程

        本文所述的互补系统最大化可消纳电量期望模型的求解步骤如下：

        步骤 1：读取基础数据并设置计算条件。包括区间流量、梯级发电计划、光伏预测出力、光伏历史预测与实际出力、分区断面约束、爬坡能力等。

        步骤 2：模型转换处理。采用 2.1 节所述模型转换方法，对非线性约束进行线性化处理。

        步骤 3：光伏出力场景构建。根据计划日光伏预测出力以及 2.2 节所述方法构建光伏出力场景。

        步骤 4：模型求解。将目标函数与转化后的约束结合构成的 MILP 模型，在 Java 环境中，编码调用CPLEX 求解类，实现模型求解，附录 Á 给出了编码和求解示例。

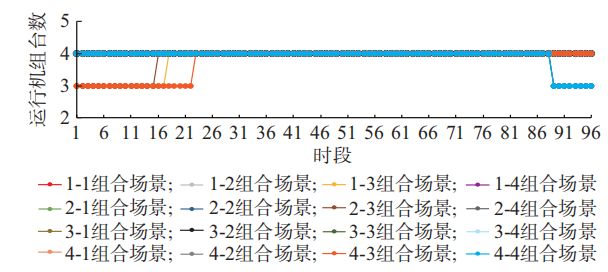
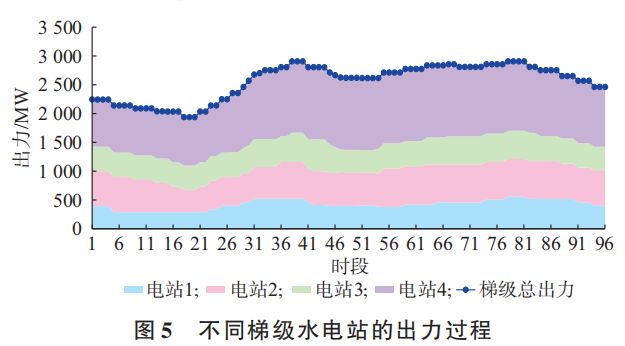
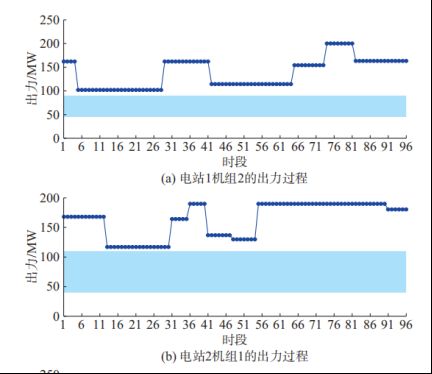
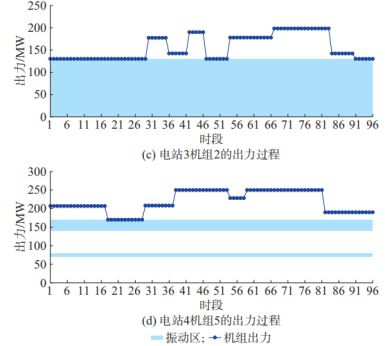
        步骤 5：结果输出。输出互补系统整体可消纳电量期望值，不同组合场景下的电站出力、机组出力、机组开停机、出库流量、水库水位等结果信息。

3.编程思路分析

3.1参数和变量定义

表1 相关参数

 

 表2 决策变量

 

3.2编程思路

        根据对文献内容的解读，可以设计下面的编程思路：

        步骤1：输入所需数据

算例分析用到的部分数据可以从原文中找到，大部分数据文献中都没有给出，只能参考其他文献进行设置。然后将所有需要的数据，按照表1的定义格式输入即可。包括区间流量、梯级发电计划、光伏预测出力、光伏历史预测与实际出力、分区断面约束、爬坡能力等。

        步骤2：光伏出力的场景生成与削减

        这部分就是根据计划日光伏预测出力以及原文中2.2节所述方法构建光伏的出力场景。原文中只是简单提到采用了参考文献[29]中所用方法进行场景生成与削减，并未详细介绍，此类方法比较简单，网上也能找到很多示例。另外，本来这个模型就是涉及非常多0-1变量，问题规模比较大，如果再加上多个场景，变量的数目将呈倍数增加，所以在复现的代码中，我就没有写场景生成与缩减的程序，直接给出了数据，选取典型的光伏出力场景作为算例。如果有需要的话可以自己修改数据，或者加入场景生成与削减的代码。

        步骤3：定义决策变量

        这一步比较简单，按照表2，初始化决策变量即可，同时每个决策变量的维度以及类型(sdpvar还是binvar)不要出错。另外，代码中变量定义的方式和文献中稍微有点不一样，这里不再详细介绍，具体可以去代码中查看。

        步骤4：写目标函数和约束条件

        写目标函数比较简单，按照给定的数据和定义的变量，写出目标函数即可。约束条件的处理比较复杂，文中只给出了约束条件16和19的线性化方法，其他几个非线性约束都是一笔带过，只说了用到某某文献中的方法。方便起见，我在这里把所有非线性约束都写出来，并介绍处理方法：

        1）式10

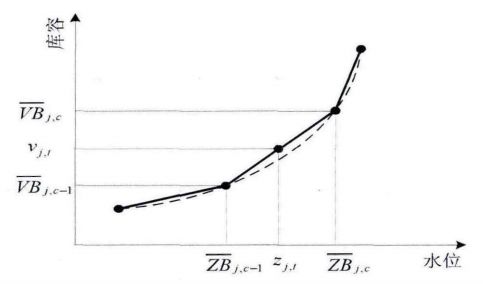
        原文中只给出了水位和库容的关系示意，一般情况下水位可以表示为库容的三次多项式，具体如下：

        四个不同的水电站水位-库容关系可以分别表示为：

y1=0.0006x^3-0.0811x^2+4.769x+1031, 10<=x<=45

y1=0.0269x^3-0.8958x^2+14.77x+891.8, 3.6<=x<=8.8

y1=0.01307x^3-0.699x^2+10.41x+803.5, 10<=x<=25

y1=0.005465x^3-0.1435x^2+3.495x+700.2, 5<=x<=22

        针对上述非线性函数关系，可采用分段线性化的方法将其转为线性约束，如图所示：

2）式11

        尾水位是泄流量的非线性函数，通常表示为泄流量的2次多项式：

        四个不同的水电站尾水位-泄流量关系可以分别表示为：

y2=7.619e-07q^2-0.000672q+976.1

y2=7.081e-08q^2-9.372e-05q+839.1

y2=7.086e-08q^2+0.00032345q+752.6

y2=1.327e-07q^2-0.0005827q+655.9

        针对上述非线性函数关系，可采用分段线性化的方法将其转为线性约束，和约束10处理方法一致。

        3）式16、19

        原文中有详细解释，此处不再赘述。

        4）式21

        约束21是一个二次约束，也可以通过分段线性化的方式转为线性约束。不再赘述。

        5）式22

        水电站的非线性出力曲线，可以表示如下：

 

为了说明采用三角权值法是如何对这个表达式进行线性化的，首先把表达式简化如下：

        假设将Q的取值范围分为n1-1个区间，区间的端点值分别为Q1,Q2,...,Qn1，将H的取值范围分为n2-1个区间，区间的端点值分别为H1,H2,...,Hn2。那么对于任意的Q和H，都可以表示为区间端点值的线性组合，例如Q的取值在Q1和Q2之间，就可以用Q1和Q2表示Q，H的取值范围在H3和H4之间，就可以用H3和H4表示H。

        我们令pij=Hi×Qj，那么表达式也可以表示为：

        下面举个例子，假设H取值范围是[10,25]，分为3个区间，区间端点分别为H1=10, H2=15, H3=20, H4=25，H取值范围是[80,100]，分为4个区间，区间端点分别为H1=80, H2=85，H3=90, H4=95, H5=100。假设H是13，Q是86，就可以写成H=0.6H1+0.4H2，Q=0.8Q2+0.2Q3，QH就可以写成(0.6H1+0.4H2)(0.8Q2+0.2Q3)。也就是λ21=0.6×0.8，λ31=0.6×0.2，λ22=0.4×0.8，λ32=0.4×0.2。因此，可以将机组的输出功率表示为变量λij和已知量pij的表达式，从非线性表达式转为线性表达式。

步骤5：求解模型

        原文中使用的是java和cplex求解，这份代码使用的是matlab+yalmip+cplex求解。

步骤6：输出结果

        按原文中的格式输出优化结果，但由于文中提供的数据非常少，大部分数据都是自己设定的，所以结果肯定不一样，但原理都是一样的。

4.Matlab代码

        完整的matlab代码可以从这个链接获取：

https://download.csdn.net/download/weixin_44209907/88130711

5.运行结果分析

5.1光伏出力曲线

 5.2运行机组台数

 

5.3梯级水电站群出力 

 

5.4水电机组出力 

 

 5.5梯级水电站水位变化

 5.6各个断面出力