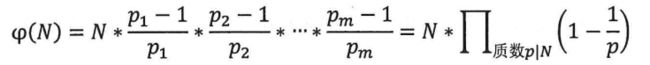c++数学知识
数学知识
1.质数判定
2.质数筛选 —— 埃氏筛,线性筛
3.质因子分解.
4.试除法求约数,倍数法求约数
5.约数个数
6.约数和
7.最大公约数
8.欧拉函数,筛法求欧拉函数
质数
质数判定
暴力试除法
bool primes(int x){
for(int i=2;i<x;i++)if(x%2==0)return 0;
return 1;
}//O(N)
暴力优化
bool primes(int x){
for(int i=2;i<=x/i;i++)if(x%2==0)return 0;
return 1;
}//O(sqrt(N))
Miller_Robbin(随机性算法,快,用不到)
typedef long long ll;
ll qpow(ll a, ll n, ll p) // 快速幂
{
ll ans = 1;
while (n)
{
if (n & 1)
ans = (__int128)ans * a % p; // 注意!中间结果可能溢出,需要使用__int128过渡
a = (__int128)a * a % p;
n >>= 1;
}
return ans;
}
bool is_prime(ll x)
{
if (x < 3) // 特判1,2
return x == 2;
if (x % 2 == 0) // 特判偶数
return false;
ll A[] = {2, 325, 9375, 28178, 450775, 9780504, 1795265022}, d = x - 1, r = 0;
while (d % 2 == 0) // 算出d, r
d /= 2, ++r;
// 或:r = __builtin_ctz(d), d >>= r;
for (auto a : A)
{
ll v = qpow(a, d, x); // a^d
// 如果a^d≡0,说明是a是x的倍数;如果a^d≡1或-1,说明这串数接下来一定都是1,不用继续计算
if (v <= 1 || v == x - 1)
continue;
for (int i = 0; i < r; ++i)
{
v = (__int128)v * v % x; // 同样使用__int128过渡
if (v == x - 1 && i != r - 1) // 得到-1,说明接下来都是1,可以退出了
{
v = 1;
break;
}
// 在中途而非开头得到1,却没有经过-1,说明存在其他数字y≠-1满足y^2≡1,则x一定不是奇素数
if (v == 1)
return false;
}
if (v != 1) // 查看是不是以1结尾
return false;
}
return true;
}//O(7*logN)对longlong范围有效
质数筛选——筛选1—N之间的所有质数
埃氏筛
int v[N];
void primes(int x){
memset(v,0,sizeof(v));
for(int i=2;i<=x;i++){
if(v[i])continue;
ans++;
cout<<i<<endl;
for(int j=1;j<=x/i;j++)v[i*j]=1;
}
}
线性筛法
int v[N],prime[N],m;
void primes(int x){
memset(v,0,sizeof(v));
m=0;
for(int i=2;i<=x;i++){
if(v[i]==0){v[i]=i;prime[++m]=i;}
for(int j=1;j<=m;j++){
if(prime[j]>v[i]||prime[j]>x/i)break;
v[i*prime[j]]=prime[j];
}
}
for(int i=1;i<=m;i++)cout<<prime[i]<<endl;
}
质因数分解
算术基本定理
试除法
int m,p[N],c[N];
void divide(int x){
m=0;
for(int i=2;i<=x/i;i++){
if(x % i == 0){
p[++m] = i, c[m]=0;
while(x%i==0)x/=i,c[m]++;
}
}
if(x>1)p[++m]=x,c[m]=1;
for(int i =1;i<=m;i++)cout<<p[i]<<"^"<<c[i]<<endl;
}
约数
试除法求约数,倍数法求约数
求N的正约数集合——试除法
int factor[1600],m=0;
for(int i=1;i<=n/i;i++){
if (n% i == 0){
factor[++m] = i;
if ( i != n/i) factor[++m] = n/i;
}
}
for(int i =1; i <= m; i++){
cout<<factor[i]<<endl;
}
试除法的推论:一个整数N的约数个数上界是2*sqrt(N)。
求1~N每个数的正约数集合——倍数法
vector<int>factor[500010];
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n / i; j++)
factor[i * j].push_back(i);
for (int i = 1; i <= n; i++) {
int tmp=factor[i].size();
for (int j = 0; j <tmp; j++)
printf("%d\n", factor[i][j]);
puts("");
}
倍数法的推论:1~N每个数的约数个数之和大约是N*logN。
最大公约数
GCD(a,b):a,b的最大公约数
int gcd(int a,int b){
return b ? gcd(b, a % b) : a;
}
互质:gcd(a,b)==1。
欧拉函数:1~N中与N互质的数的个数被称为欧拉函数即为Φ(N)。
根据欧拉函数的计算式,我们只需要分解质因数,即可顺便求出欧拉函数。
int phi(int n){
int ans=n;
for(int i = 2; i <= n/i; i++){
if (n % i == 0){
ans = ans/i * (i - 1);
while(n % i == 0)n /= i;
}
}
if(n > 1)ans = ans / n * (n - 1);
return ans;
}
推论1~2:
- 任意n>1,1~n中与n互质的数的和为n*φ(n)/2。
- 若a,b互质,这φ(ab)=φ(a)φ(b)。
积性函数
如果当 ab 互质时,有f(ab)=f(a)*f(b),那么称函数f为积性函数。