梯度下降算法

目录

梯度下降法

随机梯度下降法

实验分析

mini-batch 

---

梯度下降法

import numpy as np
import matplotlib.pyplot as plt

w = 1.0
def forward(x):
    """
    :param x: 样本数据中的每一个 x
    :return: 返回前向传播的值
    """
    print("w = ",w)
    return x * w

def cost(x_data, y_data):
    """
    :param x_data: 样本数据
    :param y_data: 样本数据
    :return: 返回len(x_data)个样本的平均损失值
    """
    cost = 0
    for x,y in zip(x_data,y_data):
        y_dict = forward(x)
        cost = cost + (y_dict - y)*(y_dict - y)
    return cost/len(x_data)

def gradient(x_data, y_data):
    """
    :param x_data: 样本数据
    :param y_data: 样本数据
    :return: 返回len(x_data)个样本的平均梯度值
    """
    grad = 0
    for x,y in zip(x_data,y_data):
        grad = grad + 2 * x * (x * w -y)
    return grad/len(x_data)

def model(x_data,y_data):
    """
    :param x_data: 样本数据
    :param y_data: 样本数据
    :return: 返回迭代次数和每一次迭代的平均损失值
    """
    global w
    epoch_list = []
    cost_list = []
    for epoch in range(100):
        cost_val = cost(x_data, y_data)
        grad_val = gradient(x_data, y_data)
        w = w - 0.01 * grad_val
        print('epoch:', epoch, 'w=', w, 'loss=', cost_val)
        epoch_list.append(epoch)
        cost_list.append(cost_val)
    return (epoch_list,cost_list)

if __name__ == "__main__":
    x_data = [1.0, 2.0, 3.0]
    y_data = [2.0, 4.0, 6.0]
    print('predict (before training)', 4, forward(4))
    epoch_list,cost_list = model(x_data,y_data)
    print('predict (after training)', 4, forward(4))
    plt.plot(epoch_list, cost_list)
    plt.ylabel('cost')
    plt.xlabel('epoch')
    plt.show()

随机梯度下降法

随机梯度下降法在神经网络中被证明是有效的。效率较低(时间复杂度较高)，学习性能较好。

随机梯度下降法和梯度下降法的主要区别在于：

1、损失函数由cost()更改为loss()。cost是计算所有训练数据的损失，loss是计算一个训练数据的损失。对应于源代码则是少了两个for循环。

2、梯度函数gradient()由计算所有训练数据的梯度更改为计算一个训练数据的梯度。

3、本算法中的随机梯度主要是指，每次拿一个训练数据来训练，然后更新梯度参数。本算法中梯度总共更新100(epoch)x3 = 300次。梯度下降法中梯度总共更新100(epoch)次。
 

import numpy as np
import matplotlib.pyplot as plt

w = 1.0
def forward(x):
    """
    :param x: 样本数据中的每一个 x
    :return: 返回前向传播的值
    """
    print("w = ",w)
    return x * w

def loss(x, y):
    """
    :param x: x_data中的每一个样本x
    :param y: y_data中的每一个样本y
    :return: 返回一个样本的损失值
    """
    y_dict = forward(x)
    return (y_dict - y)*(y_dict - y)

def gradient(x, y):
    """
    :param x: x_data中的每一个样本x
    :param y: y_data中的每一个样本y
    :return: 返回一个样本的梯度下降值
    """
    return 2 * x * (x * w - y)

def model(x_data,y_data):
    """
    :param x_data: 样本数据
    :param y_data: 样本数据
    :return: 返回迭代次数和每一个样本的损失值
    """
    global w
    epoch_list = []
    loss_list = []
    w_list = []
    for epoch in range(100):
        for x, y in zip(x_data,y_data):
            loss_val = loss(x, y)
            grad_val = gradient(x, y)
            w = w - 0.01 * grad_val
            print('epoch:', epoch, 'w=', w, 'loss=', loss_val)
        epoch_list.append(epoch)
        loss_list.append(loss_val)
        w_list.append(w)
    return (epoch_list,loss_list,w_list)

if __name__ == "__main__":
    x_data = [1.0, 2.0, 3.0]
    y_data = [2.0, 4.0, 6.0]
    print('predict (before training)', 4, forward(4))
    epoch_list,loss_list,w_list = model(x_data,y_data)
    print('predict (after training)', 4, forward(4))
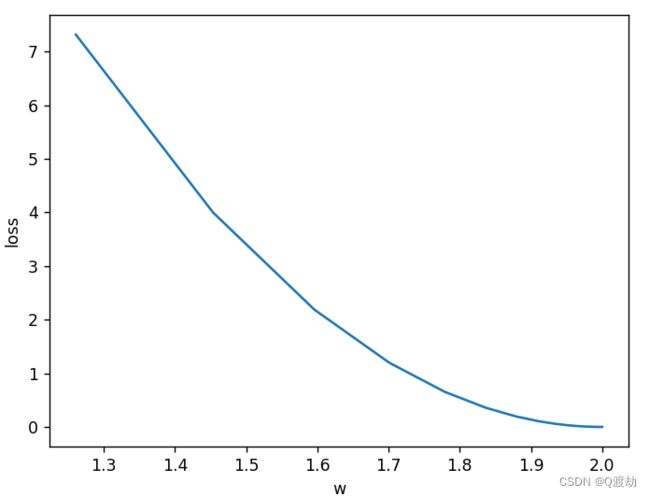
    plt.plot(w_list,loss_list)
    plt.ylabel('loss')
    plt.xlabel('w')
    plt.show()

实验分析

可以看到当 w = 2 时，找到了最优解，即有模型 y^ = 2x

mini-batch 

是对梯度下降算法和随机梯度下降算法的折中算法，既有梯度下降算法时间复杂度低的优点，也有随机梯度下降算法学习性能高的优点！所以目前深度学习算法底层的梯度下降算法大多指的是mini-batch