【机器学习07】K-Means聚类(聚类篇)
8 K-Means聚类(聚类篇)
8.1 简介
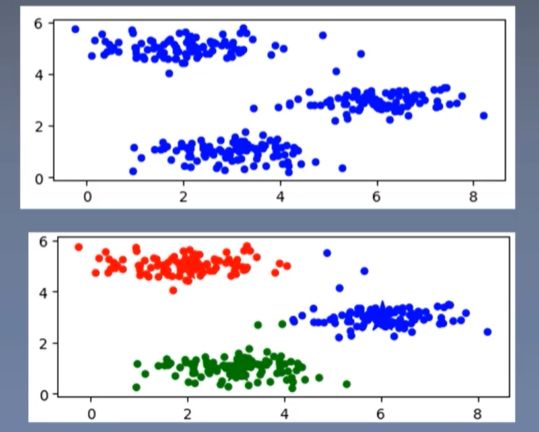
聚类(Clustering):是一种无监督学习算法,即将无分类的数据分为K类
K-Means(K-均值)聚类:选取K个初始聚类中心(质心)
步骤:
repeat:
- 对每个样本点,计算得到距其最近的质心,将其类别标为该质心所对应的cluster
- 重新计算K个cluster对应的质心
until:质心不再发生变化
8.2 距离计算公式
(1)Minkowski(闵可夫斯基距离,若p=2,则成为欧式距离)
d ( x , y ) = ( ∑ i = 1 n ∣ x i − y i ∣ p ) 1 p d\left( {x,y} \right) = {\left( {\sum\limits_{i = 1}^n {{{\left| {{x_i} - {y_i}} \right|}^p}} } \right)^{\frac{1}{p}}} d(x,y)=(i=1∑n∣xi−yi∣p)p1
(2)cosine similarity(余弦相似度):若值越大,则距离越近;反之则距离越远
s ( x , y ) = cos ( θ ) = x T y ∣ x ∣ ⋅ ∣ y ∣ = ∑ i = 1 n x i y i ∑ i = 1 n x i 2 ∑ i = 1 n y i 2 s\left( {x,y} \right) = \cos \left( \theta \right) = \frac{{{x^T}y}}{{\left| x \right| \cdot \left| y \right|}} = \frac{{\sum\limits_{i = 1}^n {{x_i}{y_i}} }}{{\sqrt {\sum\limits_{i = 1}^n {x_i^2} } \sqrt {\sum\limits_{i = 1}^n {y_i^2} } }} s(x,y)=cos(θ)=∣x∣⋅∣y∣xTy=i=1∑nxi2i=1∑nyi2i=1∑nxiyi
(3)Pearson coefficient(皮尔逊相关系数):值在[-1,1]之间,若值越接近于1则越相关(距离越近);反之则越不相关(距离越远)
p ( x , y ) = c o v ( x , y ) σ x σ y = ∑ i = 1 n ( x i − μ x ) ( y i − μ y ) ∑ i = 1 n ( x i − μ x ) 2 ∑ i = 1 n ( y i − μ y ) 2 p(x,y) = \frac{{{\mathop{\rm cov}} (x,y)}}{{{\sigma _x}{\sigma _y}}} = \frac{{\sum\limits_{i = 1}^n {({x_i} - {\mu _x})({y_i} - {\mu _y})} }}{{\sqrt {\sum\limits_{i = 1}^n {{{({x_i} - {\mu _x})}^2}} } \sqrt {\sum\limits_{i = 1}^n {{{({y_i} - {\mu _y})}^2}} } }} p(x,y)=σxσycov(x,y)=i=1∑n(xi−μx)2i=1∑n(yi−μy)2i=1∑n(xi−μx)(yi−μy)
K-Means代码实现:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
def loaddata():
data = np.loadtxt('data/cluster_data.csv',delimiter=',')
return data
X = loaddata()
# 散点图
plt.scatter(X[:, 0], X[:, 1], s=20)
# 随机初始化聚类中心(质心)
def kMeansInitCentroids(X, K):
# 从X的数据中随机取k个作为质心
index = np.random.randint(0,len(X)-1,K)
return X[index]
# 计算数据点到聚类中心(质心)的距离,并判断该数据点属于哪个质心(哪一个类别)
def findClosestCentroids(X, centroids):
# idx中数据表明对应X的样本数据是属于哪一个质心(哪一个类别)
idx = np.zeros(len(X)).reshape(X.shape[0],-1)
for i in range(len(X)):
minDistance = float('inf'); # 初始无限大
index = 0
for k in range(len(centroids)):
# 距离计算:使用欧式距离
distance = np.sum(np.power(X[i]-centroids[k],2))
if(distance<minDistance):
minDistance = distance
index = k
idx[i]=index
return idx
# 重新计算聚类中心(质心)
def computeCentroids(X, idx):
K = set(np.ravel(idx).tolist()) # 找到所有聚类中心索引
K = list(K)
centroids = np.ndarray((len(K),X.shape[1]))
for i in range(len(K)):
# 选择数据X中类别为k[i]的数据
data = X[np.where(idx==K[i])[0]]
# 重新计算聚类中心
# axis:设置轴,axis=0:按列运算
centroids[i] = np.sum(data,axis=0)/len(data)
return centroids
# K-Means算法
def K_Means(X, K, max_iters):
# 初始化聚类中心(质心)
initial_centroids = kMeansInitCentroids(X,K)
# 迭代
for i in range(max_iters):
if i==0:
centroids = initial_centroids
# 计算样本到质心的距离,并返回每个样本所属的质心
idx = findClosestCentroids(X, centroids)
# 重新计算聚类中心(质心)
centroids = computeCentroids(X, idx)
return idx,centroids
idx,centroids = K_Means(X, 3, 8)
print("X中属于的类别:",idx)
print("聚类中心(质心):",centroids)
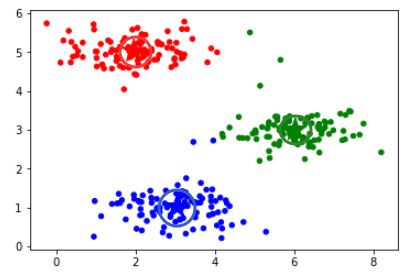
# 可视化
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
# c=np.ravel(idx):根据idx的取值匹配cmp属性来设置颜色
plt.scatter(X[:, 0], X[:, 1], c=np.ravel(idx), cmap=cm_dark, s=20)
# c=np.arange(len(centroids)):根据centroidsd的取值匹配cmp属性来设置颜色
plt.scatter(centroids[:, 0], centroids[:, 1], c=np.arange(len(centroids)), cmap=cm_dark, marker='*', s=500)
plt.show()
8.3 Sklearn之K-means聚类
K-Means相关API:
# sklearn库
from sklearn.cluster import KMeans
# 创建模型(定义K-Means聚类)
model=KMeans(n_clusters=聚类中心(质心)个数,max_iter=最大迭代次数)
# 训练模型
# 输入:一个二维数组表示的样本矩阵
# 输出:每个样本最终的结果
model.fit(输入)
print("聚类中心(质心):",model.cluster_centers_)
print("每个样本所属的簇(类别):",model.labels_)
案例:加载cluster_data.csv数据文件,基于sklearn库实现K-Means聚类模型
import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
# sklearn库
from sklearn.cluster import KMeans
def loaddata():
data = np.loadtxt('data/cluster_data.csv',delimiter=',')
return data
X = loaddata()
# 散点图
plt.scatter(X[:, 0], X[:, 1], s=20)
# 创建模型(定义K-Means聚类)
model=KMeans(n_clusters=3,max_iter=10)
# 训练模型
model.fit(X)
print("聚类中心(质心):",model.cluster_centers_)
print("每个样本所属的簇(类别):",model.labels_)
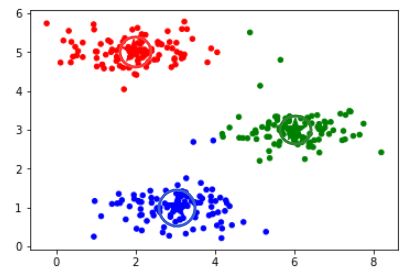
# 可视化
cm_dark = mpl.colors.ListedColormap(['g', 'r','b'])
# c=model.labels_:根据model.labels_的取值匹配cmp属性来设置颜色
plt.scatter(X[:, 0], X[:, 1], c=model.labels_, cmap=cm_dark, s=20)
# c=np.arange(len(model.cluster_centers_)):根据model.cluster_centers_的取值匹配cmp属性来设置颜色
plt.scatter(model.cluster_centers_[:, 0], model.cluster_centers_[:, 1], c=np.arange(len(model.cluster_centers_)), cmap=cm_dark, marker='*', s=500)
plt.show()
8.4 案例:亚洲足球队聚类分析
import numpy as np
import pandas as pd
# sklearn库
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler
# 读取csv文件,并添加列索引
df = pd.read_csv("data/football_team_data.csv",index_col="国家")
print(df)
# 获取数据
X = df.values
# 数据标准化
X = StandardScaler().fit_transform(X)
# 创建模型(定义K-Means)
model = KMeans(n_clusters=3,max_iter=10)
# 训练模型
model.fit(X)
# 添加新的一列来存放聚类结果标签
df["聚类"]=model.labels_
print(df)