Linux内核中红黑树节点的插入原理分析
红黑树是一种特化的AVL树(平衡二叉树),都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡,从而获得较高的查找性能。它虽然是复杂的,但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的: 它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目。普通的二叉查找树在极端情况下可退化成链表,此时的增删查效率比较低。平衡的二叉树(如AVL、红黑树等)能较好的解决这个问题。
一、红黑树的性质
1,每个结点是红的或黑的
2,根结点是黑的
3,每个叶子结点是黑的
4,如果一个结点是红的,则它的两个儿子都是黑的
5,对每个结点,从该结点到其子孙结点所有路径上的包含相同数目的黑结点
二、红黑树结构体的定义
红黑树的定义在/include/linux/rbtree.h中实现:
struct rb_node {
unsigned long __rb_parent_color;
struct rb_node *rb_right;
struct rb_node *rb_left;
} __attribute__((aligned(sizeof(long))));
/* The alignment might seem pointless, but allegedly CRIS needs it */
struct rb_root {
struct rb_node *rb_node;
};
成员rb_parent_color同时存储两种数据,一是其双亲结点的地址,另一是此结点的着色。attribute((aligned(sizeof(long))))属性保证了红黑树中的每个结点的首地址都是32位对齐的(在32位机上),也就是说每个结点首地址的bit[1]和bit[0]都是0,因此就可以使用bit[0]来存储结点的颜色属性而不干扰到其双亲结点首地址的存储。
三、红黑树节点的插入
红黑树使用时的插入方法在Documentation/rbtree.txt文件内有定义:
int my_insert(struct rb_root *root, struct mytype *data)
{
struct rb_node **new = &(root->rb_node), *parent = NULL;
/* Figure out where to put new node */
while (*new) {
struct mytype *this = container_of(*new, struct mytype, node);
int result = strcmp(data->keystring, this->keystring);
parent = *new;
if (result < 0)
new = &((*new)->rb_left);
else if (result > 0)
new = &((*new)->rb_right);
else
return FALSE;
}
/* Add new node and rebalance tree. */
rb_link_node(&data->node, parent, new);
rb_insert_color(&data->node, root);
return TRUE;
}
这个函数主要有三个步骤:
第一,搜索新节点要插入的位置。
第二,初始化新节点。
第三、将新节点插入到红黑树内。
2.1、搜索新节点要插入的位置
搜索新节点要插入的位置,主要是比较新节点的数据和已知红黑树的节点大小,从而判断出位置。
2.2、初始化新节点
初始化新节点调用的是函数:
static inline void rb_link_node(struct rb_node * node, struct rb_node * parent,
struct rb_node ** rb_link)
该函数在linux/include/linux/rbtree.h文件内定义
static inline void rb_link_node(struct rb_node * node, struct rb_node * parent,
struct rb_node ** rb_link)
{
node->__rb_parent_color = (unsigned long)parent;
node->rb_left = node->rb_right = NULL;
*rb_link = node;
}
在linux/include/linux/rbtree_augmented.h文件内有如下定义
#define RB_RED 0
#define RB_BLACK 1
所以当在一个红黑树插入一个节点时初始化此节点的颜色为红色。
2.3、将新节点插入到红黑树内
rb_insert_color是供外部调用的插入函数,真正实现插入算法的函数是__rb_insert。该函数在文件linux/lib/rbtree.c文件内:
static __always_inline void
__rb_insert(struct rb_node *node, struct rb_root *root,
void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
struct rb_node *parent = rb_red_parent(node), *gparent, *tmp;
while (true) {
/*
* Loop invariant: node is red
*
* If there is a black parent, we are done.
* Otherwise, take some corrective action as we don't
* want a red root or two consecutive red nodes.
*/
/* while 循环退出的条件:(1)寻找到根节点 (2)parent 为黑色 */
//---------------------------------------------------------- 情况1 & 情况2
if (!parent) {
rb_set_parent_color(node, NULL, RB_BLACK);
break;
} else if (rb_is_black(parent))
break;
/* 到了这里,node 的父节点颜色一定是 Red */
gparent = rb_red_parent(parent);
tmp = gparent->rb_right;
if (parent != tmp) { /* parent == gparent->rb_left */
if (tmp && rb_is_red(tmp)) {
//-------------------------------------------------- 情况3
/*
* Case 1 - color flips
*
* G g
* / \ / \
* p u --> P U
* / /
* n n
*
* However, since g's parent might be red, and
* 4) does not allow this, we need to recurse
* at g.
*/
rb_set_parent_color(tmp, gparent, RB_BLACK);
rb_set_parent_color(parent, gparent, RB_BLACK);
node = gparent;
parent = rb_parent(node);
rb_set_parent_color(node, parent, RB_RED);
continue;
}
tmp = parent->rb_right;
if (node == tmp) {
//-------------------------------------------------- 情况4
/*
* Case 2 - left rotate at parent
*
* G G
* / \ / \
* p U --> n U
* \ /
* n p
*
* This still leaves us in violation of 4), the
* continuation into Case 3 will fix that.
*/
parent->rb_right = tmp = node->rb_left;
node->rb_left = parent;
if (tmp)
rb_set_parent_color(tmp, parent,
RB_BLACK);
rb_set_parent_color(parent, node, RB_RED);
augment_rotate(parent, node);
parent = node;
tmp = node->rb_right;
}
//------------------------------------------------------ 情况5
/*
* Case 3 - right rotate at gparent
*
* G P
* / \ / \
* p U --> n g
* / \
* n U
*/
gparent->rb_left = tmp; /* == parent->rb_right */
parent->rb_right = gparent;
if (tmp)
rb_set_parent_color(tmp, gparent, RB_BLACK);
__rb_rotate_set_parents(gparent, parent, root, RB_RED);
augment_rotate(gparent, parent);
break;
} else {
tmp = gparent->rb_left;
if (tmp && rb_is_red(tmp)) {
/* Case 1 - color flips */
rb_set_parent_color(tmp, gparent, RB_BLACK);
rb_set_parent_color(parent, gparent, RB_BLACK);
node = gparent;
parent = rb_parent(node);
rb_set_parent_color(node, parent, RB_RED);
continue;
}
tmp = parent->rb_left;
if (node == tmp) {
/* Case 2 - right rotate at parent */
parent->rb_left = tmp = node->rb_right;
node->rb_right = parent;
if (tmp)
rb_set_parent_color(tmp, parent,
RB_BLACK);
rb_set_parent_color(parent, node, RB_RED);
augment_rotate(parent, node);
parent = node;
tmp = node->rb_left;
}
/* Case 3 - left rotate at gparent */
gparent->rb_right = tmp; /* == parent->rb_left */
parent->rb_left = gparent;
if (tmp)
rb_set_parent_color(tmp, gparent, RB_BLACK);
__rb_rotate_set_parents(gparent, parent, root, RB_RED);
augment_rotate(gparent, parent);
break;
}
}
}
当在一个红黑树插入一个节点时初始化此节点的颜色为红色,但如果新节点父节点也为红色,将会违背红黑树的性质:一条路径上不能出现相邻的两个红色节点。这时就要根据具体的情况进行分析处理,根据穷举的方法,有下面五种情况,通过这五种情况的不同操作来使红黑树保持平衡。
2.3.1、情况1
当前红黑树为空,即插入的节点是根节点。此时需要将节点的颜色由红色变为黑色以满足性质2。

代码为:
if (!parent) {
rb_set_parent_color(node, NULL, RB_BLACK);
break;
}
当寻找到根节点时退出while循环。
2.3.2、情况2
插入节点N的父节点P为黑色,此时满足性质4和性质5,不需要调整。
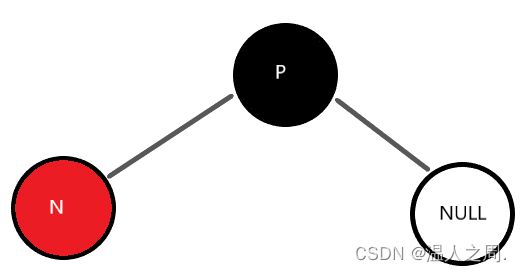
代码为:
else if (rb_is_black(parent))
break;
2.3.3、情况3
插入节点N的父节点P是红色,叔叔节点U也是红色,由性质4得P和U的父节点G为黑色。
此时由于N和P均为红色,破坏了性质4,需要进行调整。这种情况下,先将P和U的颜色染成黑色,再将G的颜色染成红色。此时经过G路径上的黑色节点的数量不变,性质5仍然满足。但需要注意的是G染成红色后,可能和它的父节点形成连续的红色节点,此时需要递归向上调整。
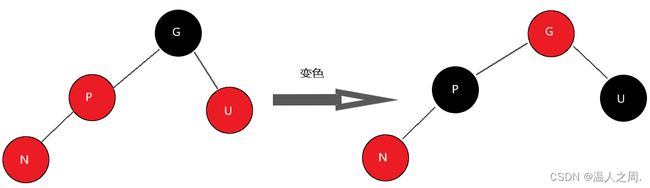
代码为
tmp = gparent->rb_right;//祖父节点的右孩子
if (parent != tmp) { /* parent == gparent->rb_left *///父节点是祖父节点的左孩子
if (tmp && rb_is_red(tmp)) {//叔节点不为空,且叔节点为红色(此时父节点为红色)
/*
* Case 1 - color flips
*
* G g
* / \ / \
* p u --> P U
* / /
* n n
*
* However, since g's parent might be red, and
* 4) does not allow this, we need to recurse
* at g.
*/
rb_set_parent_color(tmp, gparent, RB_BLACK);//设置叔节点为黑色
rb_set_parent_color(parent, gparent, RB_BLACK);//设置父节点为黑色
node = gparent;
parent = rb_parent(node);
rb_set_parent_color(node, parent, RB_RED);//设置祖父节点为红色
continue;//向上递归循环调整
}
以上代码是新插入节点N在其祖父节点G的左子树的情况,右子树情况对称同理。
2.3.4、情况4
插入节点N的父节点为红色,叔叔节点U为黑色。节点N是P的右孩子,且节点P是G的左孩子。
此时先对节点P进行左旋,调整N与P的位置。接下来按照情况5来处理,以满足性质4。
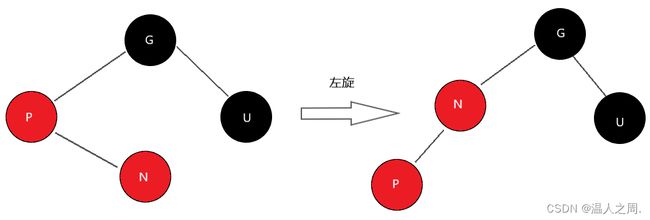
代码为
tmp = parent->rb_right;//父节点的右孩子
if (node == tmp) {//节点为父节点的右孩子
/*
* Case 2 - left rotate at parent
*
* G G
* / \ / \
* p U --> n U
* \ /
* n p
*
* This still leaves us in violation of 4), the
* continuation into Case 3 will fix that.
*/
parent->rb_right = tmp = node->rb_left;//将节点的左孩子,赋值给temp和父节点的右孩子(之前父节点的右孩子为该节点)
node->rb_left = parent;//将父节点赋值为节点的左孩子
if (tmp)//如果赋值前该节点存在左孩子
rb_set_parent_color(tmp, parent,
RB_BLACK);//将运算前节点左孩子(也是运算后父节点的右孩子变为黑色),
rb_set_parent_color(parent, node, RB_RED);//设置父节点为红色
augment_rotate(parent, node);
parent = node;//将父节点赋值为该节点
tmp = node->rb_right;
}
2.3.5、情况5
某次调整后,子树中节点N的父节点为红色,叔叔节点U为黑色。节点N是P的左孩子,且节点P是G的左孩子。
此时对G进行右旋,调整P和G的位置,并交换颜色。使得性质4被满足。

代码为
/*
* Case 3 - right rotate at gparent
*
* G P
* / \ / \
* p U --> n g
* / \
* n U
*/
gparent->rb_left = tmp; /* == parent->rb_right */
parent->rb_right = gparent;
if (tmp)
rb_set_parent_color(tmp, gparent, RB_BLACK);
__rb_rotate_set_parents(gparent, parent, root, RB_RED);
augment_rotate(gparent, parent);
break;
四、红黑树节点插入的实例流程分析
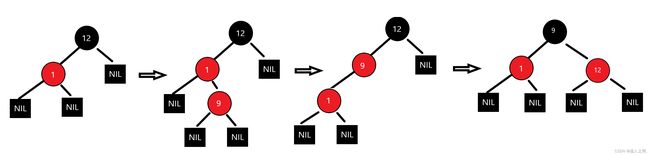
通过插入12 1 9 2 0 完成红黑树流程分析。
4.1、添加12

说明:符合2.3章节的情况一,添加的节点若是根节点,则直接将其设置为黑色。
4.2、添加1
搜索新节点1要插入的位置为根节点的左子叶,且初始化为红色,则直接添加。

说明:符合2.3章节的情况二,插入节点N的父节点P为黑色,不需要调整。
4.3、添加9
调整红黑树步骤:
第一步、符合2.3章节的情况四,插入节点9的父节点1为红色,叔叔节点U为黑色。节点9是1的右孩子,且节点1是12的左孩子。此时先对节点1进行左旋,调整1与9的位置。
第二步、符合2.3章节的情况五,子树中节点1的父节点9为红色,叔叔节点U为黑色。节点1是9的左孩子,且节点9是节点12的左孩子。
此时对节点12进行右旋,调整节点9和节点12的位置,并交换颜色。
4.4、添加2
搜索新节点2要插入的位置为节点1右子叶。

调整红黑树步骤:
第一步、符合2.3章节的情况三,插入节点2的父节点1是红色,叔叔节点12也是红色,此时由于节点2和节点1均为红色,破坏了性质4,需要进行调整。这种情况下,先将节点1和节点12的颜色染成黑色,再将节点9的颜色染成红色。此时经过节点9路径上的黑色节点的数量不变,性质5仍然满足。
第二步、符合2.3章节的情况一,节点9为根节点,将节点9设为黑色。
4.5、添加0
搜索新节点0要插入的位置为节点1左子叶。

此时,不需要调整,已经是一课红黑树。
以此类推,所有红黑树节点的添加,皆遵循以上流程。