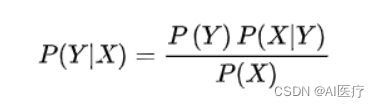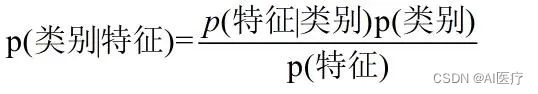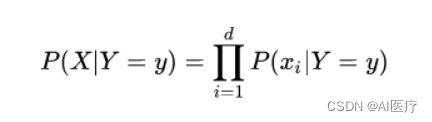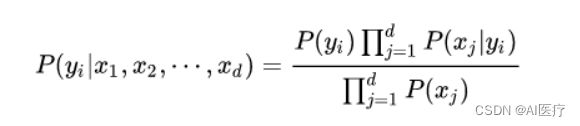机器学习之朴素贝叶斯（Naive Bayes）

1 朴素贝叶斯算法介绍

朴素贝叶斯是经典的机器学习算法之一，也是为数不多的基于概率论的分类算法。朴素贝叶斯分类器(Naive Bayes Classifier 或 NBC)发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率，是应用最为广泛的分类算法之一。

朴素贝叶斯方法是在贝叶斯算法的基础上进行了相应的简化，即假定给定目标值时属性之间相互条件独立。虽然这个简化方式在一定程度上降低了贝叶斯分类算法的分类效果，但是在实际的应用场景中，极大地简化了贝叶斯方法的复杂性。

朴素贝叶斯对于给定的训练集，首先基于特征条件独立假设学习输入输出的联合概率分布；然后基于此模型，对给定的输入 x，利用贝叶斯定理求出后验概率最大的输出 y。

 

1.1 贝叶斯

贝叶斯是英国数学家。1702年出生于伦敦，贝叶斯在数学方面主要研究概率论。对于统计决策函数、统计推断、统计的估算等做出了贡献。他的统计学概率理论称为贝叶斯Thomas Bayes。在贝叶斯之前，人们已经能够计算“正向概率”，如“假设袋子里面有 N 个白球，M 个黑球，你伸手进去摸一把，摸出黑球的概率是M/(M+N)”。而一个自然而然的问题是反过来：“如果我们事先并不知道袋子里面黑白球的比例，而是闭着眼睛摸出一个（或好几个）球，观察这些取出来的球的颜色之后，那么我们可以就此对袋子里面的黑白球的比例作出什么样的推测”。这个问题，就是所谓的逆向概率问题。贝叶斯就是为解决这种逆向概率而生。

1.2 概率

（1）先验概率

通过经验判断事情发生的概率，P(A)是 A 的先验概率，之所以称为“先验”是因为它不考虑任何 B 方面的因素。

（2）后验概率

发生结果后，推测原因的概率。属于条件概率的一种，贝叶斯就是用来解决后验概率。
P(A|B)是已知 B 发生后 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。p(房地产|垃圾邮件）代表垃圾邮件中房地产出现的频率。

（3）条件概率

事件A在另一个事件B已经发生的条件下发生的概率，表示P(A|B)

1.3 贝叶斯公式

设有样本数据集D={d1,d2,...,dn}，对应样本数据的特征属性集为X={x1,x2,...,xd}类变量为Y={y1,y2,...ym} ，即D可以分为ym类别。其中{x1,x2,...,xd} 相互独立且随机，则Y的先验概率P(Y) ，Y的后验概率P(Y|X) ，由朴素贝叶斯算法可得，后验概率可以由先验概率P(Y) ,证据P(X) ,类条件概率P(X|Y)计算出

 在分类算法里面应用，可以转换成下面的表达式

 朴素贝叶斯基于各特征之间相互独立，在给定类别为y的情况下，上式可以进一步表示为下式：

 由于P(X)的大小是固定不变的，因此在比较后验概率时，只比较上式的分子部分即可,因此可以得到一个样本数据属于类别yi的朴素贝叶斯计算：

 

2 朴素贝叶斯算法的优缺点

朴素贝叶斯算法是一种基于概率统计的分类算法，它假设特征之间相互独立，并利用贝叶斯定理进行分类。该算法具有以下优点和缺点：

2.1 朴素贝叶斯算法优点：

• 简单高效：朴素贝叶斯算法的计算速度相对较快，训练和预测的时间复杂度较低。它的实现也相对简单，不需要大量的参数调整。

• 处理高维数据：朴素贝叶斯算法在处理高维数据时表现良好。由于假设特征之间独立，算法能够处理大量特征的情况，并且不容易受到维度灾难的影响。

• 对小样本数据有效：即使在小样本情况下，朴素贝叶斯算法也能够表现出较好的分类性能。由于它利用概率估计来进行分类，可以更好地利用有限的训练数据。

• 处理分类和文本特征：朴素贝叶斯算法在处理分类问题和文本分类问题时具有优势。它能够对文本特征进行建模，并在文本分类、垃圾邮件过滤等任务中取得良好的效果。

2.2 朴素贝叶斯算法缺点：

• 特征独立性假设：朴素贝叶斯算法假设特征之间相互独立，但在实际情况中，很多特征可能存在相关性。这种独立性假设可能导致模型的准确性下降。

• 对数据分布的假设：朴素贝叶斯算法假设特征的概率分布为高斯分布或多项式分布等。如果数据的真实分布与这些假设不符，模型的表现可能会受到影响。

• 欠拟合问题：由于特征独立性假设，朴素贝叶斯算法可能无法准确地捕捉特征之间的复杂关系。在某些情况下，它可能会出现欠拟合问题，导致分类性能不佳。

• 缺乏调节参数的能力：朴素贝叶斯算法的参数通常是根据训练数据进行估计的，缺乏自适应调节的能力。这意味着它可能无法灵活地适应不同类型的数据和分类任务。

尽管朴素贝叶斯算法存在一些限制，但它在许多实际应用中仍然表现出色，特别是在文本分类和简单分类问题上。在特征独立性假设适用且数据量较小的情况下，朴素贝叶斯算法是一个简单而有效的选择。

3 朴素贝叶斯算法的应用场景

朴素贝叶斯算法在许多领域和应用中都有广泛的应用。以下是一些常见的应用场景：

• 文本分类：朴素贝叶斯算法在文本分类任务中表现出色。它可以用于垃圾邮件过滤、情感分析、新闻分类等。通过对文本特征进行建模，可以将文本数据自动分类到不同的类别。

• 电子商务推荐系统：朴素贝叶斯算法可以用于电子商务推荐系统中的商品分类和个性化推荐。通过对用户历史购买数据和商品特征进行建模，可以预测用户对新商品的喜好，并向其推荐相关的商品。

• 垃圾邮件过滤：由于朴素贝叶斯算法在处理文本分类任务中的优秀表现，它被广泛应用于垃圾邮件过滤。通过训练模型，可以自动识别垃圾邮件，并将其过滤出来，提高用户的邮件使用体验。

• 文本生成与自然语言处理：朴素贝叶斯算法可用于文本生成和自然语言处理任务，如语言模型和词性标注。通过对语料库中的文本进行学习，可以建立一个模型来生成新的文本或对文本进行标注。

• 疾病诊断：朴素贝叶斯算法在医学领域中的应用也很广泛。它可以用于疾病诊断，通过对患者的症状和医学测试结果进行建模，预测患者可能患有的疾病，并辅助医生做出诊断决策。

• 图像分类：尽管朴素贝叶斯算法在处理图像数据方面的表现不如其他深度学习方法，但它仍然可以用于简单的图像分类任务。通过对图像特征进行建模，可以将图像自动分类到不同的类别。

需要注意的是，朴素贝叶斯算法在处理复杂关系和高维数据上可能存在限制，适用于特征独立性假设适用的情况下。在现实应用中，通常会将朴素贝叶斯算法与其他算法和技术相结合，以提高分类的准确性和性能。

4 基于朴素贝叶斯对新闻数据进行分类

4.1 代码实现

# 朴素贝叶斯算法
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.model_selection import train_test_split


def nb_news():
    """
    用朴素贝叶斯算法对新闻进行分类
    """
    # 1.获取数据
    news = fetch_20newsgroups(subset="all")

    # 2.划分数据集
    x_train, x_test, y_train, y_test = train_test_split(news.data, news.target, test_size=0.25)

    # 3.特征工程：文本特征抽取-tfidf
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4.朴素贝叶斯算法预估器流程
    estimator = MultinomialNB()
    estimator.fit(x_train, y_train)

    # 5.模型评估
    # 方法1：直接比对真实值和预测值
    y_predict = estimator.predict(x_test)
    print(f"文章类型/预测类型：{y_test}/{y_predict}\n")

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print(f"预测准确率为：{score}\n")

    return None


if __name__ == "__main__":
    # 用朴素贝叶斯算法对新闻进行分类
    nb_news()

4.2 结果展示

文章类型:2,预测类型：2
文章类型:12,预测类型：12
文章类型:0,预测类型：0
文章类型:2,预测类型：2
文章类型:14,预测类型：14
文章类型:4,预测类型：4
文章类型:3,预测类型：3
文章类型:12,预测类型：12
文章类型:15,预测类型：15
文章类型:2,预测类型：2
文章类型:16,预测类型：16
文章类型:6,预测类型：6
文章类型:11,预测类型：11
文章类型:2,预测类型：2
文章类型:7,预测类型：7
文章类型:3,预测类型：3
文章类型:5,预测类型：5
文章类型:4,预测类型：4
文章类型:14,预测类型：14
文章类型:8,预测类型：8
文章类型:14,预测类型：14
文章类型:1,预测类型：1
文章类型:11,预测类型：11
文章类型:13,预测类型：13
文章类型:8,预测类型：8
文章类型:4,预测类型：4
文章类型:7,预测类型：7
文章类型:17,预测类型：17
文章类型:7,预测类型：7
文章类型:5,预测类型：2
文章类型:7,预测类型：7
文章类型:0,预测类型：0
文章类型:13,预测类型：13
文章类型:12,预测类型：12

预测准确率为：0.8478353140916808

最终的预测准确率达到84.7%