32.利用fmincon 解决 最小费用问题(matlab程序)
1.简述
fmincon函数非线性约束下的最优化问题
fmincon函数,既是求最小约束非线性多变量函数
该函数被用于求如下函数的最小值
语法如下:
x = fmincon(fun,x0,A,b)
x = fmincon(fun,x0,A,b,Aeq,beq)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fmincon(problem)
[x,fval] = fmincon(…)
[x,fval,exitflag] = fmincon(…)
[x,fval,exitflag,output] = fmincon(…)
[x,fval,exitflag,output,lambda] = fmincon(…)
[x,fval,exitflag,output,lambda,grad]= fmincon(…)
[x,fval,exitflag,output,lambda,grad,hessian]= fmincon(…)
对于fmincon函数,其exitflag参数中的数字:
1、一阶最优性条件满足容许范围
2、X的变化小于容许范围
3、目标函数的变化小于容许范围
4、重要搜索方向小于规定的容许范围并且约束违背小于options.TolCon
5、重要方向导数小于规定的容许范围并且约束违背小于options.TolCon
0、到达最大迭代次数或到达函数评价
-1、算法由输出函数终止
-2、无可行点
、
2.代码
主函数:
%% 最小费用问题
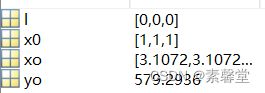
x0=[1,1,1];
l=zeros(1,3);
[xo,yo]=fmincon('f1219',x0,[],[],[],[],l,[],'fcon1219')
子函数:
function [X,FVAL,EXITFLAG,OUTPUT,LAMBDA,GRAD,HESSIAN] = fmincon(FUN,X,A,B,Aeq,Beq,LB,UB,NONLCON,options,varargin)
%FMINCON finds a constrained minimum of a function of several variables.
% FMINCON attempts to solve problems of the form:
% min F(X) subject to: A*X <= B, Aeq*X = Beq (linear constraints)
% X C(X) <= 0, Ceq(X) = 0 (nonlinear constraints)
% LB <= X <= UB (bounds)
%
% FMINCON implements four different algorithms: interior point, SQP,
% active set, and trust region reflective. Choose one via the option
% Algorithm: for instance, to choose SQP, set OPTIONS =
% optimoptions('fmincon','Algorithm','sqp'), and then pass OPTIONS to
% FMINCON.
%
% X = FMINCON(FUN,X0,A,B) starts at X0 and finds a minimum X to the
% function FUN, subject to the linear inequalities A*X <= B. FUN accepts
% input X and returns a scalar function value F evaluated at X. X0 may be
% a scalar, vector, or matrix.
%
% X = FMINCON(FUN,X0,A,B,Aeq,Beq) minimizes FUN subject to the linear
% equalities Aeq*X = Beq as well as A*X <= B. (Set A=[] and B=[] if no
% inequalities exist.)
%
% X = FMINCON(FUN,X0,A,B,Aeq,Beq,LB,UB) defines a set of lower and upper
% bounds on the design variables, X, so that a solution is found in
% the range LB <= X <= UB. Use empty matrices for LB and UB
% if no bounds exist. Set LB(i) = -Inf if X(i) is unbounded below;
% set UB(i) = Inf if X(i) is unbounded above.
%
% X = FMINCON(FUN,X0,A,B,Aeq,Beq,LB,UB,NONLCON) subjects the minimization
% to the constraints defined in NONLCON. The function NONLCON accepts X
% and returns the vectors C and Ceq, representing the nonlinear
% inequalities and equalities respectively. FMINCON minimizes FUN such
% that C(X) <= 0 and Ceq(X) = 0. (Set LB = [] and/or UB = [] if no bounds
% exist.)
%
% X = FMINCON(FUN,X0,A,B,Aeq,Beq,LB,UB,NONLCON,OPTIONS) minimizes with
% the default optimization parameters replaced by values in OPTIONS, an
% argument created with the OPTIMOPTIONS function. See OPTIMOPTIONS for
% details. For a list of options accepted by FMINCON refer to the
% documentation.
%
% X = FMINCON(PROBLEM) finds the minimum for PROBLEM. PROBLEM is a
% structure with the function FUN in PROBLEM.objective, the start point
% in PROBLEM.x0, the linear inequality constraints in PROBLEM.Aineq
% and PROBLEM.bineq, the linear equality constraints in PROBLEM.Aeq and
% PROBLEM.beq, the lower bounds in PROBLEM.lb, the upper bounds in
% PROBLEM.ub, the nonlinear constraint function in PROBLEM.nonlcon, the
% options structure in PROBLEM.options, and solver name 'fmincon' in
% PROBLEM.solver. Use this syntax to solve at the command line a problem
% exported from OPTIMTOOL.
%
% [X,FVAL] = FMINCON(FUN,X0,...) returns the value of the objective
% function FUN at the solution X.
%
% [X,FVAL,EXITFLAG] = FMINCON(FUN,X0,...) returns an EXITFLAG that
% describes the exit condition. Possible values of EXITFLAG and the
% corresponding exit conditions are listed below. See the documentation
% for a complete description.
%
% All algorithms:
% 1 First order optimality conditions satisfied.
% 0 Too many function evaluations or iterations.
% -1 Stopped by output/plot function.
% -2 No feasible point found.
% Trust-region-reflective, interior-point, and sqp:
% 2 Change in X too small.
% Trust-region-reflective:
% 3 Change in objective function too small.
% Active-set only:
% 4 Computed search direction too small.
% 5 Predicted change in objective function too small.
% Interior-point and sqp:
% -3 Problem seems unbounded.
%
% [X,FVAL,EXITFLAG,OUTPUT] = FMINCON(FUN,X0,...) returns a structure
% OUTPUT with information such as total number of iterations, and final
% objective function value. See the documentation for a complete list.
%
% [X,FVAL,EXITFLAG,OUTPUT,LAMBDA] = FMINCON(FUN,X0,...) returns the
% Lagrange multipliers at the solution X: LAMBDA.lower for LB,
% LAMBDA.upper for UB, LAMBDA.ineqlin is for the linear inequalities,
% LAMBDA.eqlin is for the linear equalities, LAMBDA.ineqnonlin is for the
% nonlinear inequalities, and LAMBDA.eqnonlin is for the nonlinear
% equalities.
%
% [X,FVAL,EXITFLAG,OUTPUT,LAMBDA,GRAD] = FMINCON(FUN,X0,...) returns the
% value of the gradient of FUN at the solution X.
%
% [X,FVAL,EXITFLAG,OUTPUT,LAMBDA,GRAD,HESSIAN] = FMINCON(FUN,X0,...)
% returns the value of the exact or approximate Hessian of the Lagrangian
% at X.
%
% Examples
% FUN can be specified using @:
% X = fmincon(@humps,...)
% In this case, F = humps(X) returns the scalar function value F of
% the HUMPS function evaluated at X.
%
% FUN can also be an anonymous function:
% X = fmincon(@(x) 3*sin(x(1))+exp(x(2)),[1;1],[],[],[],[],[0 0])
% returns X = [0;0].
%
% If FUN or NONLCON are parameterized, you can use anonymous functions to
% capture the problem-dependent parameters. Suppose you want to minimize
% the objective given in the function myfun, subject to the nonlinear
% constraint mycon, where these two functions are parameterized by their
% second argument a1 and a2, respectively. Here myfun and mycon are
% MATLAB file functions such as
%
% function f = myfun(x,a1)
% f = x(1)^2 + a1*x(2)^2;
%
% function [c,ceq] = mycon(x,a2)
% c = a2/x(1) - x(2);
% ceq = [];
%
% To optimize for specific values of a1 and a2, first assign the values
% to these two parameters. Then create two one-argument anonymous
% functions that capture the values of a1 and a2, and call myfun and
% mycon with two arguments. Finally, pass these anonymous functions to
% FMINCON:
%
% a1 = 2; a2 = 1.5; % define parameters first
% options = optimoptions('fmincon','Algorithm','interior-point'); % run interior-point algorithm
% x = fmincon(@(x) myfun(x,a1),[1;2],[],[],[],[],[],[],@(x) mycon(x,a2),options)
%
% See also OPTIMOPTIONS, OPTIMTOOL, FMINUNC, FMINBND, FMINSEARCH, @, FUNCTION_HANDLE.
% Copyright 1990-2018 The MathWorks, Inc.
defaultopt = struct( ...
'Algorithm','interior-point', ...
'AlwaysHonorConstraints','bounds', ...
'DerivativeCheck','off', ...
'Diagnostics','off', ...
'DiffMaxChange',Inf, ...
'DiffMinChange',0, ...
'Display','final', ...
'FinDiffRelStep', [], ...
'FinDiffType','forward', ...
'ProblemdefOptions', struct, ...
'FunValCheck','off', ...
'GradConstr','off', ...
'GradObj','off', ...
'HessFcn',[], ...
'Hessian',[], ...
'HessMult',[], ...
'HessPattern','sparse(ones(numberOfVariables))', ...
'InitBarrierParam',0.1, ...
'InitTrustRegionRadius','sqrt(numberOfVariables)', ...
'MaxFunEvals',[], ...
'MaxIter',[], ...
'MaxPCGIter',[], ...
'MaxProjCGIter','2*(numberOfVariables-numberOfEqualities)', ...
'MaxSQPIter','10*max(numberOfVariables,numberOfInequalities+numberOfBounds)', ...
'ObjectiveLimit',-1e20, ...
'OutputFcn',[], ...
'PlotFcns',[], ...
'PrecondBandWidth',0, ...
'RelLineSrchBnd',[], ...
'RelLineSrchBndDuration',1, ...
'ScaleProblem','none', ...
'SubproblemAlgorithm','ldl-factorization', ...
'TolCon',1e-6, ...
'TolConSQP',1e-6, ...
'TolFun',1e-6, ...
'TolFunValue',1e-6, ...
'TolPCG',0.1, ...
'TolProjCG',1e-2, ...
'TolProjCGAbs',1e-10, ...
'TolX',[], ...
'TypicalX','ones(numberOfVariables,1)', ...
'UseParallel',false ...
);
% If just 'defaults' passed in, return the default options in X
if nargin==1 && nargout <= 1 && strcmpi(FUN,'defaults')
X = defaultopt;
return
end
if nargin < 10
options = [];
if nargin < 9
NONLCON = [];
if nargin < 8
UB = [];
if nargin < 7
LB = [];
if nargin < 6
Beq = [];
if nargin < 5
Aeq = [];
if nargin < 4
B = [];
if nargin < 3
A = [];
end
end
end
end
end
end
end
end
if nargin == 1
if isa(FUN,'struct')
[FUN,X,A,B,Aeq,Beq,LB,UB,NONLCON,options] = separateOptimStruct(FUN);
else % Single input and non-structure.
error(message('optimlib:fmincon:InputArg'));
end
end
% No options passed. Set options directly to defaultopt after
allDefaultOpts = isempty(options);
% Prepare the options for the solver
options = prepareOptionsForSolver(options, 'fmincon');
% Check for non-double inputs
msg = isoptimargdbl('FMINCON', {'X0','A','B','Aeq','Beq','LB','UB'}, ...
X, A, B, Aeq, Beq, LB, UB);
if ~isempty(msg)
error('optimlib:fmincon:NonDoubleInput',msg);
end
% Check for complex X0
if ~isreal(X)
error('optimlib:fmincon:ComplexX0', ...
getString(message('optimlib:commonMsgs:ComplexX0','Fmincon')));
end
% Set options to default if no options were passed.
if allDefaultOpts
% Options are all default
options = defaultopt;
end
if nargout > 4
computeLambda = true;
else
computeLambda = false;
end
activeSet = 'active-set';
sqp = 'sqp';
trustRegionReflective = 'trust-region-reflective';
interiorPoint = 'interior-point';
sqpLegacy = 'sqp-legacy';
sizes.xShape = size(X);
XOUT = X(:);
sizes.nVar = length(XOUT);
% Check for empty X
if sizes.nVar == 0
error(message('optimlib:fmincon:EmptyX'));
end
display = optimget(options,'Display',defaultopt,'fast',allDefaultOpts);
flags.detailedExitMsg = contains(display,'detailed');
switch display
case {'off','none'}
verbosity = 0;
case {'notify','notify-detailed'}
verbosity = 1;
case {'final','final-detailed'}
verbosity = 2;
case {'iter','iter-detailed'}
verbosity = 3;
case 'testing'
verbosity = 4;
otherwise
verbosity = 2;
end
% Set linear constraint right hand sides to column vectors
% (in particular, if empty, they will be made the correct
% size, 0-by-1)
B = B(:);
Beq = Beq(:);
% Check for consistency of linear constraints, before evaluating
% (potentially expensive) user functions
% Set empty linear constraint matrices to the correct size, 0-by-n
if isempty(Aeq)
Aeq = reshape(Aeq,0,sizes.nVar);
end
if isempty(A)
A = reshape(A,0,sizes.nVar);
end
[lin_eq,Aeqcol] = size(Aeq);
[lin_ineq,Acol] = size(A);
% These sizes checks assume that empty matrices have already been made the correct size
if Aeqcol ~= sizes.nVar
error(message('optimlib:fmincon:WrongNumberOfColumnsInAeq', sizes.nVar))
end
if lin_eq ~= length(Beq)
error(message('optimlib:fmincon:AeqAndBeqInconsistent'))
end
if Acol ~= sizes.nVar
error(message('optimlib:fmincon:WrongNumberOfColumnsInA', sizes.nVar))
end
if lin_ineq ~= length(B)
error(message('optimlib:fmincon:AeqAndBinInconsistent'))
end
% End of linear constraint consistency check
Algorithm = optimget(options,'Algorithm',defaultopt,'fast',allDefaultOpts);
% Option needed for processing initial guess
AlwaysHonorConstraints = optimget(options,'AlwaysHonorConstraints',defaultopt,'fast',allDefaultOpts);
% Determine algorithm user chose via options. (We need this now
% to set OUTPUT.algorithm in case of early termination due to
% inconsistent bounds.)
if ~any(strcmpi(Algorithm,{activeSet, sqp, trustRegionReflective, interiorPoint, sqpLegacy}))
error(message('optimlib:fmincon:InvalidAlgorithm'));
end
OUTPUT.algorithm = Algorithm;
[XOUT,l,u,msg] = checkbounds(XOUT,LB,UB,sizes.nVar);
if ~isempty(msg)
EXITFLAG = -2;
[FVAL,LAMBDA,GRAD,HESSIAN] = deal([]);
OUTPUT.iterations = 0;
OUTPUT.funcCount = 0;
OUTPUT.stepsize = [];
if strcmpi(OUTPUT.algorithm,activeSet) || strcmpi(OUTPUT.algorithm,sqp)|| strcmpi(OUTPUT.algorithm,sqpLegacy)
OUTPUT.lssteplength = [];
else % trust-region-reflective, interior-point
OUTPUT.cgiterations = [];
end
if strcmpi(OUTPUT.algorithm,interiorPoint) || strcmpi(OUTPUT.algorithm,activeSet) || ...
strcmpi(OUTPUT.algorithm,sqp) || strcmpi(OUTPUT.algorithm,sqpLegacy)
OUTPUT.constrviolation = [];
end
OUTPUT.firstorderopt = [];
OUTPUT.message = msg;
X(:) = XOUT;
if verbosity > 0
disp(msg)
end
return
end
% Get logical list of finite lower and upper bounds
finDiffFlags.hasLBs = isfinite(l);
finDiffFlags.hasUBs = isfinite(u);
lFinite = l(finDiffFlags.hasLBs);
uFinite = u(finDiffFlags.hasUBs);
% Create structure of flags and initial values, initialize merit function
% type and the original shape of X.
flags.meritFunction = 0;
initVals.xOrigShape = X;
diagnostics = strcmpi(optimget(options,'Diagnostics',defaultopt,'fast',allDefaultOpts),'on');
funValCheck = strcmpi(optimget(options,'FunValCheck',defaultopt,'fast',allDefaultOpts),'on');
derivativeCheck = strcmpi(optimget(options,'DerivativeCheck',defaultopt,'fast',allDefaultOpts),'on');
% Gather options needed for finitedifferences
% Write checked DiffMaxChange, DiffMinChage, FinDiffType, FinDiffRelStep,
% GradObj and GradConstr options back into struct for later use
options.DiffMinChange = optimget(options,'DiffMinChange',defaultopt,'fast',allDefaultOpts);
options.DiffMaxChange = optimget(options,'DiffMaxChange',defaultopt,'fast',allDefaultOpts);
if options.DiffMinChange >= options.DiffMaxChange
error(message('optimlib:fmincon:DiffChangesInconsistent', sprintf( '%0.5g', options.DiffMinChange ), sprintf( '%0.5g', options.DiffMaxChange )))
end
% Read in and error check option TypicalX
[typicalx,ME] = getNumericOrStringFieldValue('TypicalX','ones(numberOfVariables,1)', ...
ones(sizes.nVar,1),'a numeric value',options,defaultopt);
if ~isempty(ME)
throw(ME)
end
checkoptionsize('TypicalX', size(typicalx), sizes.nVar);
options.TypicalX = typicalx;
options.FinDiffType = optimget(options,'FinDiffType',defaultopt,'fast',allDefaultOpts);
options = validateFinDiffRelStep(sizes.nVar,options,defaultopt);
options.GradObj = optimget(options,'GradObj',defaultopt,'fast',allDefaultOpts);
options.GradConstr = optimget(options,'GradConstr',defaultopt,'fast',allDefaultOpts);
flags.grad = strcmpi(options.GradObj,'on');
% Notice that defaultopt.Hessian = [], so the variable "hessian" can be empty
hessian = optimget(options,'Hessian',defaultopt,'fast',allDefaultOpts);
% If calling trust-region-reflective with an unavailable Hessian option value,
% issue informative error message
if strcmpi(OUTPUT.algorithm,trustRegionReflective) && ...
~( isempty(hessian) || strcmpi(hessian,'on') || strcmpi(hessian,'user-supplied') || ...
strcmpi(hessian,'off') || strcmpi(hessian,'fin-diff-grads') )
error(message('optimlib:fmincon:BadTRReflectHessianValue'))
end
if ~iscell(hessian) && ( strcmpi(hessian,'user-supplied') || strcmpi(hessian,'on') )
flags.hess = true;
else
flags.hess = false;
end
if isempty(NONLCON)
flags.constr = false;
else
flags.constr = true;
end
% Process objective function
if ~isempty(FUN) % will detect empty string, empty matrix, empty cell array
% constrflag in optimfcnchk set to false because we're checking the objective, not constraint
funfcn = optimfcnchk(FUN,'fmincon',length(varargin),funValCheck,flags.grad,flags.hess,false,Algorithm);
else
error(message('optimlib:fmincon:InvalidFUN'));
end
% Process constraint function
if flags.constr % NONLCON is non-empty
flags.gradconst = strcmpi(options.GradConstr,'on');
% hessflag in optimfcnchk set to false because hessian is never returned by nonlinear constraint
% function
%
% constrflag in optimfcnchk set to true because we're checking the constraints
confcn = optimfcnchk(NONLCON,'fmincon',length(varargin),funValCheck,flags.gradconst,false,true);
else
flags.gradconst = false;
confcn = {'','','','',''};
end
[rowAeq,colAeq] = size(Aeq);
if strcmpi(OUTPUT.algorithm,activeSet) || strcmpi(OUTPUT.algorithm,sqp) || strcmpi(OUTPUT.algorithm,sqpLegacy)
% See if linear constraints are sparse and if user passed in Hessian
if issparse(Aeq) || issparse(A)
warning(message('optimlib:fmincon:ConvertingToFull', Algorithm))
end
if flags.hess % conflicting options
flags.hess = false;
warning(message('optimlib:fmincon:HessianIgnoredForAlg', Algorithm));
if strcmpi(funfcn{1},'fungradhess')
funfcn{1}='fungrad';
elseif strcmpi(funfcn{1},'fun_then_grad_then_hess')
funfcn{1}='fun_then_grad';
end
end
elseif strcmpi(OUTPUT.algorithm,trustRegionReflective)
% Look at constraint type and supplied derivatives, and determine if
% trust-region-reflective can solve problem
isBoundedNLP = isempty(NONLCON) && isempty(A) && isempty(Aeq); % problem has only bounds and no other constraints
isLinEqNLP = isempty(NONLCON) && isempty(A) && isempty(lFinite) ...
&& isempty(uFinite) && colAeq > rowAeq;
if isBoundedNLP && flags.grad
% if only l and u then call sfminbx
elseif isLinEqNLP && flags.grad
% if only Aeq beq and Aeq has more columns than rows, then call sfminle
else
linkToDoc = addLink('Choosing the Algorithm', 'optim', 'helptargets.map', ...
'choose_algorithm', false);
if ~isBoundedNLP && ~isLinEqNLP
error(message('optimlib:fmincon:ConstrTRR', linkToDoc))
else
% The user has a problem that satisfies the TRR constraint
% restrictions but they haven't supplied gradients.
error(message('optimlib:fmincon:GradOffTRR', linkToDoc))
end
end
end
% Process initial point
shiftedX0 = false; % boolean that indicates if initial point was shifted
if any(strcmpi(OUTPUT.algorithm,{activeSet,sqp, sqpLegacy}))
if strcmpi(OUTPUT.algorithm,sqpLegacy)
% Classify variables: finite lower bounds, finite upper bounds
xIndices = classifyBoundsOnVars(l,u,sizes.nVar,false);
end
% Check that initial point strictly satisfies the bounds on the variables.
violatedLowerBnds_idx = XOUT(finDiffFlags.hasLBs) < l(finDiffFlags.hasLBs);
violatedUpperBnds_idx = XOUT(finDiffFlags.hasUBs) > u(finDiffFlags.hasUBs);
if any(violatedLowerBnds_idx) || any(violatedUpperBnds_idx)
finiteLbIdx = find(finDiffFlags.hasLBs);
finiteUbIdx = find(finDiffFlags.hasUBs);
XOUT(finiteLbIdx(violatedLowerBnds_idx)) = l(finiteLbIdx(violatedLowerBnds_idx));
XOUT(finiteUbIdx(violatedUpperBnds_idx)) = u(finiteUbIdx(violatedUpperBnds_idx));
X(:) = XOUT;
shiftedX0 = true;
end
elseif strcmpi(OUTPUT.algorithm,trustRegionReflective)
%
% If components of initial x not within bounds, set those components
% of initial point to a "box-centered" point
%
if isempty(Aeq)
arg = (u >= 1e10); arg2 = (l <= -1e10);
u(arg) = inf;
l(arg2) = -inf;
xinitOutOfBounds_idx = XOUT < l | XOUT > u;
if any(xinitOutOfBounds_idx)
shiftedX0 = true;
XOUT = startx(u,l,XOUT,xinitOutOfBounds_idx);
X(:) = XOUT;
end
else
% Phase-1 for sfminle nearest feas. pt. to XOUT. Don't print a
% message for this change in X0 for sfminle.
XOUT = feasibl(Aeq,Beq,XOUT);
X(:) = XOUT;
end
elseif strcmpi(OUTPUT.algorithm,interiorPoint)
% Variables: fixed, finite lower bounds, finite upper bounds
xIndices = classifyBoundsOnVars(l,u,sizes.nVar,true);
% If honor bounds mode, then check that initial point strictly satisfies the
% simple inequality bounds on the variables and exactly satisfies fixed variable
% bounds.
if strcmpi(AlwaysHonorConstraints,'bounds') || strcmpi(AlwaysHonorConstraints,'bounds-ineqs')
violatedFixedBnds_idx = XOUT(xIndices.fixed) ~= l(xIndices.fixed);
violatedLowerBnds_idx = XOUT(xIndices.finiteLb) <= l(xIndices.finiteLb);
violatedUpperBnds_idx = XOUT(xIndices.finiteUb) >= u(xIndices.finiteUb);
if any(violatedLowerBnds_idx) || any(violatedUpperBnds_idx) || any(violatedFixedBnds_idx)
XOUT = shiftInitPtToInterior(sizes.nVar,XOUT,l,u,Inf);
X(:) = XOUT;
shiftedX0 = true;
end
end
end
% Display that x0 was shifted in order to honor bounds
if shiftedX0
if verbosity >= 3
if strcmpi(OUTPUT.algorithm,interiorPoint)
fprintf(getString(message('optimlib:fmincon:ShiftX0StrictInterior')));
fprintf('\n');
else
fprintf(getString(message('optimlib:fmincon:ShiftX0ToBnds')));
fprintf('\n');
end
end
end
% Evaluate function
initVals.g = zeros(sizes.nVar,1);
HESSIAN = [];
switch funfcn{1}
case 'fun'
try
initVals.f = feval(funfcn{3},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:ObjectiveError', ...
getString(message('optimlib:fmincon:ObjectiveError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
case 'fungrad'
try
[initVals.f,initVals.g] = feval(funfcn{3},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:ObjectiveError', ...
getString(message('optimlib:fmincon:ObjectiveError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
case 'fungradhess'
try
[initVals.f,initVals.g,HESSIAN] = feval(funfcn{3},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:ObjectiveError', ...
getString(message('optimlib:fmincon:ObjectiveError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
case 'fun_then_grad'
try
initVals.f = feval(funfcn{3},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:ObjectiveError', ...
getString(message('optimlib:fmincon:ObjectiveError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
try
initVals.g = feval(funfcn{4},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:GradientError', ...
getString(message('optimlib:fmincon:GradientError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
case 'fun_then_grad_then_hess'
try
initVals.f = feval(funfcn{3},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:ObjectiveError', ...
getString(message('optimlib:fmincon:ObjectiveError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
try
initVals.g = feval(funfcn{4},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:GradientError', ...
getString(message('optimlib:fmincon:GradientError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
try
HESSIAN = feval(funfcn{5},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:HessianError', ...
getString(message('optimlib:fmincon:HessianError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
otherwise
error(message('optimlib:fmincon:UndefinedCallType'));
end
% Check that the objective value is a scalar
if numel(initVals.f) ~= 1
error(message('optimlib:fmincon:NonScalarObj'))
end
% Check that the objective gradient is the right size
initVals.g = initVals.g(:);
if numel(initVals.g) ~= sizes.nVar
error('optimlib:fmincon:InvalidSizeOfGradient', ...
getString(message('optimlib:commonMsgs:InvalidSizeOfGradient',sizes.nVar)));
end
% Evaluate constraints
switch confcn{1}
case 'fun'
try
[ctmp,ceqtmp] = feval(confcn{3},X,varargin{:});
catch userFcn_ME
if strcmpi('MATLAB:maxlhs',userFcn_ME.identifier)
error(message('optimlib:fmincon:InvalidHandleNonlcon'))
else
optim_ME = MException('optimlib:fmincon:NonlconError', ...
getString(message('optimlib:fmincon:NonlconError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
end
initVals.ncineq = ctmp(:);
initVals.nceq = ceqtmp(:);
initVals.gnc = zeros(sizes.nVar,length(initVals.ncineq));
initVals.gnceq = zeros(sizes.nVar,length(initVals.nceq));
case 'fungrad'
try
[ctmp,ceqtmp,initVals.gnc,initVals.gnceq] = feval(confcn{3},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:NonlconError', ...
getString(message('optimlib:fmincon:NonlconError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
initVals.ncineq = ctmp(:);
initVals.nceq = ceqtmp(:);
case 'fun_then_grad'
try
[ctmp,ceqtmp] = feval(confcn{3},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:NonlconError', ...
getString(message('optimlib:fmincon:NonlconError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
initVals.ncineq = ctmp(:);
initVals.nceq = ceqtmp(:);
try
[initVals.gnc,initVals.gnceq] = feval(confcn{4},X,varargin{:});
catch userFcn_ME
optim_ME = MException('optimlib:fmincon:NonlconFunOrGradError', ...
getString(message('optimlib:fmincon:NonlconFunOrGradError')));
userFcn_ME = addCause(userFcn_ME,optim_ME);
rethrow(userFcn_ME)
end
case ''
% No nonlinear constraints. Reshaping of empty quantities is done later
% in this file, where both cases, (i) no nonlinear constraints and (ii)
% nonlinear constraints that have one type missing (equalities or
% inequalities), are handled in one place
initVals.ncineq = [];
initVals.nceq = [];
initVals.gnc = [];
initVals.gnceq = [];
otherwise
error(message('optimlib:fmincon:UndefinedCallType'));
end
% Check for non-double data typed values returned by user functions
if ~isempty( isoptimargdbl('FMINCON', {'f','g','H','c','ceq','gc','gceq'}, ...
initVals.f, initVals.g, HESSIAN, initVals.ncineq, initVals.nceq, initVals.gnc, initVals.gnceq) )
error('optimlib:fmincon:NonDoubleFunVal',getString(message('optimlib:commonMsgs:NonDoubleFunVal','FMINCON')));
end
sizes.mNonlinEq = length(initVals.nceq);
sizes.mNonlinIneq = length(initVals.ncineq);
% Make sure empty constraint and their derivatives have correct sizes (not 0-by-0):
if isempty(initVals.ncineq)
initVals.ncineq = reshape(initVals.ncineq,0,1);
end
if isempty(initVals.nceq)
initVals.nceq = reshape(initVals.nceq,0,1);
end
if isempty(initVals.gnc)
initVals.gnc = reshape(initVals.gnc,sizes.nVar,0);
end
if isempty(initVals.gnceq)
initVals.gnceq = reshape(initVals.gnceq,sizes.nVar,0);
end
[cgrow,cgcol] = size(initVals.gnc);
[ceqgrow,ceqgcol] = size(initVals.gnceq);
if cgrow ~= sizes.nVar || cgcol ~= sizes.mNonlinIneq
error(message('optimlib:fmincon:WrongSizeGradNonlinIneq', sizes.nVar, sizes.mNonlinIneq))
end
if ceqgrow ~= sizes.nVar || ceqgcol ~= sizes.mNonlinEq
error(message('optimlib:fmincon:WrongSizeGradNonlinEq', sizes.nVar, sizes.mNonlinEq))
end
if diagnostics
% Do diagnostics on information so far
diagnose('fmincon',OUTPUT,flags.grad,flags.hess,flags.constr,flags.gradconst,...
XOUT,sizes.mNonlinEq,sizes.mNonlinIneq,lin_eq,lin_ineq,l,u,funfcn,confcn);
end
% Create default structure of flags for finitedifferences:
% This structure will (temporarily) ignore some of the features that are
% algorithm-specific (e.g. scaling and fault-tolerance) and can be turned
% on later for the main algorithm.
finDiffFlags.fwdFinDiff = strcmpi(options.FinDiffType,'forward');
finDiffFlags.scaleObjConstr = false; % No scaling for now
finDiffFlags.chkFunEval = false; % No fault-tolerance yet
finDiffFlags.chkComplexObj = false; % No need to check for complex values
finDiffFlags.isGrad = true; % Scalar objective
% For parallel finite difference (if needed) we need to send the function
% handles now to the workers. This avoids sending the function handles in
% every iteration of the solver. The output from 'setOptimFcnHandleOnWorkers'
% is a onCleanup object that will perform cleanup task on the workers.
UseParallel = optimget(options,'UseParallel',defaultopt,'fast',allDefaultOpts);
ProblemdefOptions = optimget(options, 'ProblemdefOptions',defaultopt,'fast',allDefaultOpts);
FromSolve = false;
if ~isempty(ProblemdefOptions) && isfield(ProblemdefOptions, 'FromSolve')
FromSolve = ProblemdefOptions.FromSolve;
end
cleanupObj = setOptimFcnHandleOnWorkers(UseParallel,funfcn,confcn,FromSolve);
% Check derivatives
if derivativeCheck && ... % User wants to check derivatives...
(flags.grad || ... % of either objective or ...
flags.gradconst && sizes.mNonlinEq+sizes.mNonlinIneq > 0) % nonlinear constraint function.
validateFirstDerivatives(funfcn,confcn,X, ...
l,u,options,finDiffFlags,sizes,varargin{:});
end
% Flag to determine whether to look up the exit msg.
flags.makeExitMsg = logical(verbosity) || nargout > 3;
% call algorithm
if strcmpi(OUTPUT.algorithm,activeSet) % active-set
defaultopt.MaxIter = 400; defaultopt.MaxFunEvals = '100*numberofvariables'; defaultopt.TolX = 1e-6;
defaultopt.Hessian = 'off';
problemInfo = []; % No problem related data
[X,FVAL,LAMBDA,EXITFLAG,OUTPUT,GRAD,HESSIAN]=...
nlconst(funfcn,X,l,u,full(A),B,full(Aeq),Beq,confcn,options,defaultopt, ...
finDiffFlags,verbosity,flags,initVals,problemInfo,varargin{:});
elseif strcmpi(OUTPUT.algorithm,trustRegionReflective) % trust-region-reflective
if (strcmpi(funfcn{1}, 'fun_then_grad_then_hess') || strcmpi(funfcn{1}, 'fungradhess'))
Hstr = [];
elseif (strcmpi(funfcn{1}, 'fun_then_grad') || strcmpi(funfcn{1}, 'fungrad'))
n = length(XOUT);
Hstr = optimget(options,'HessPattern',defaultopt,'fast',allDefaultOpts);
if ischar(Hstr)
if strcmpi(Hstr,'sparse(ones(numberofvariables))')
Hstr = sparse(ones(n));
else
error(message('optimlib:fmincon:InvalidHessPattern'))
end
end
checkoptionsize('HessPattern', size(Hstr), n);
end
defaultopt.MaxIter = 400; defaultopt.MaxFunEvals = '100*numberofvariables'; defaultopt.TolX = 1e-6;
defaultopt.Hessian = 'off';
% Trust-region-reflective algorithm does not compute constraint
% violation as it progresses. If the user requests the output structure,
% we need to calculate the constraint violation at the returned
% solution.
if nargout > 3
computeConstrViolForOutput = true;
else
computeConstrViolForOutput = false;
end
if isempty(Aeq)
defaultopt.MaxPCGIter = 'max(1,floor(numberOfVariables/2))';
[X,FVAL,LAMBDA,EXITFLAG,OUTPUT,GRAD,HESSIAN] = ...
sfminbx(funfcn,X,l,u,verbosity,options,defaultopt,computeLambda,initVals.f,initVals.g, ...
HESSIAN,Hstr,flags.detailedExitMsg,computeConstrViolForOutput,flags.makeExitMsg,varargin{:});
else
defaultopt.MaxPCGIter = [];
[X,FVAL,LAMBDA,EXITFLAG,OUTPUT,GRAD,HESSIAN] = ...
sfminle(funfcn,X,sparse(Aeq),Beq,verbosity,options,defaultopt,computeLambda,initVals.f, ...
initVals.g,HESSIAN,Hstr,flags.detailedExitMsg,computeConstrViolForOutput,flags.makeExitMsg,varargin{:});
end
elseif strcmpi(OUTPUT.algorithm,interiorPoint)
defaultopt.MaxIter = 1000; defaultopt.MaxFunEvals = 3000; defaultopt.TolX = 1e-10;
defaultopt.Hessian = 'bfgs';
mEq = lin_eq + sizes.mNonlinEq + nnz(xIndices.fixed); % number of equalities
% Interior-point-specific options. Default values for lbfgs memory is 10, and
% ldl pivot threshold is 0.01
options = getIpOptions(options,sizes.nVar,mEq,flags.constr,defaultopt,10,0.01);
[X,FVAL,EXITFLAG,OUTPUT,LAMBDA,GRAD,HESSIAN] = barrier(funfcn,X,A,B,Aeq,Beq,l,u,confcn,options.HessFcn, ...
initVals.f,initVals.g,initVals.ncineq,initVals.nceq,initVals.gnc,initVals.gnceq,HESSIAN, ...
xIndices,options,finDiffFlags,flags.makeExitMsg,varargin{:});
elseif strcmpi(OUTPUT.algorithm,sqp)
defaultopt.MaxIter = 400; defaultopt.MaxFunEvals = '100*numberofvariables';
defaultopt.TolX = 1e-6; defaultopt.Hessian = 'bfgs';
% Validate options used by sqp
options = getSQPOptions(options,defaultopt,sizes.nVar);
% Call algorithm
[X,FVAL,EXITFLAG,OUTPUT,LAMBDA,GRAD,HESSIAN] = sqpInterface(funfcn,X,full(A),full(B),full(Aeq),full(Beq), ...
full(l),full(u),confcn,initVals.f,full(initVals.g),full(initVals.ncineq),full(initVals.nceq), ...
full(initVals.gnc),full(initVals.gnceq),sizes,options,finDiffFlags,verbosity,flags.makeExitMsg,varargin{:});
else % sqpLegacy
defaultopt.MaxIter = 400; defaultopt.MaxFunEvals = '100*numberofvariables';
defaultopt.TolX = 1e-6; defaultopt.Hessian = 'bfgs';
% Validate options used by sqp
options = getSQPOptions(options,defaultopt,sizes.nVar);
% Call algorithm
[X,FVAL,EXITFLAG,OUTPUT,LAMBDA,GRAD,HESSIAN] = sqpLineSearch(funfcn,X,full(A),full(B),full(Aeq),full(Beq), ...
full(l),full(u),confcn,initVals.f,full(initVals.g),full(initVals.ncineq),full(initVals.nceq), ...
full(initVals.gnc),full(initVals.gnceq),xIndices,options,finDiffFlags, ...
verbosity,flags.detailedExitMsg,flags.makeExitMsg,varargin{:});
end
% Force a cleanup of the handle object. Sometimes, MATLAB may
% delay the cleanup but we want to be sure it is cleaned up.
delete(cleanupObj);
3.运行结果