二分图算法（染色法 匈牙利算法）

---

二分图算法总览

二分图的概念

1.二分图的定义

一个图 $G=(V,E)$ 被称为二分图（Bipartite Graph），当且仅当顶点集 $V$ 可以分割成两个互不相交的子集 $U$ 和 $W$，使得 $E$ 中的每一条边都连接一个 $U$ 中的顶点和一个 $W$ 中的顶点。

换句话说，二分图就是图中的顶点可以分成两类，每条边都只连接这两类顶点中的一个。

例如：


这就是一个明显的二分图，集合A与B中的点互不相连。

2.二分图的特点

1. 图 $G$ 中的顶点可以分成两个互不相交的子集 $U$ 和 $W$，$V=U\cup W$。
2. 对于任意一条边 $(u,w)$，必有 $u\in U$，$w\in W$。也就是说，每条边都连接 $U$ 和 $W$ 中的顶点。
3. 不存在属于同一顶点集的两点之间有边相连。$U$ 中的顶点只连接 $W$ 中的顶点，$W$ 中的顶点只连接 $U$ 中的顶点。
4. 一个图是二分图，当且仅当它不包含奇数长度的环。

注意：

• 二分图当且仅当图中没有奇数环
• 当图中没有奇数环一定是二分图
• 任何无回路的图均是二分图
  
• 二分图不一定是连通图

3.二分图的应用

二分图的一些常见应用场景包括:

1. 匹配问题
   二分图可以用于描述匹配关系。例如,在求解Stable Marriage问题时，男生集合和女生集合构成二分图的两个顶点集，边表示男生和女生之间的偏好。求解这个二分图的最大匹配，就可以得到一个稳定的匹配方案。

2. 网络流问题
   很多网络流问题可以建模为二分图。例如在网络最大流问题中，源点集和汇点集分别作为二分图的两个顶点集，边和边上的流量构成二分图。求解这个二分图的最大流就等价于求原网络的最大流。

3. 图的着色问题
   如果将每个颜色看成一个顶点集，图的节点看成另一个顶点集，则图的着色问题可以转换为在对应的二分图中求最大匹配。

4. 关系建模
   二分图可以建模表达两个不同类型实体集合之间的关系。例如，学生-课程的关系可以用学生集合和课程集合构成的二分图来表示。

5. 调度问题
   将任务看成一个顶点集，处理器资源看成另一个顶点集，二分图的边表示任务和处理器之间的关系，求解二分图的最大匹配可以用于调度资源。

染色法（判断二分图）

染色法是判断图是否为二分图的一种算法。

基本思想是:

①为图 $G$ 中的每个顶点赋予红色或蓝色这两种不同的颜色。

②如果存在一条边的两个端点颜色相同，则该图不是二分图。

③如果所有的边两端点颜色均不同，则该图是二分图。

算法步骤

1. 创建一个标记数组 $color[]$，将所有顶点标记为未染色，初始化为 $0$。

2. 遍历所有顶点，对于每个未染色的顶点 $v$：
   (1) 使用红色或蓝色对其染色，$color[v]=1$ 或 $2$。
   (2) 将与顶点 $v$ 相连的所有顶点染成不同颜色。

3. 检查每条边的两个端点颜色是否不同：
   (1) 若存在一条边其两个端点颜色相同，则返回 false，该图不是二分图。
   (2) 若所有边两端点颜色均不同，则返回 true，该图是二分图。

分析：

• 时间复杂度 $O(n+m)$，需要遍历所有顶点和边。
• 空间复杂度 $O(n)$，需要颜色标记数组。
• 可以在线性时间内判断二分图，效率较高。

算法运用

染色法判定二分图

题目描述：
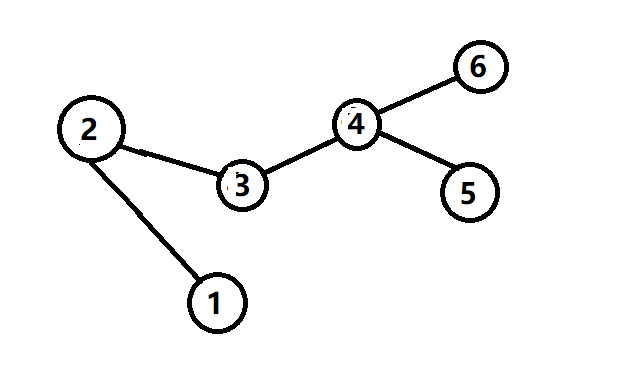
给定一个 $n$ 个点 $m$ 条边的无向图，图中可能存在重边和自环。

请你判断这个图是否是二分图。

输入格式：
第一行包含两个整数 $n$ 和 $m$。

接下来 $m$ 行，每行包含两个整数 $u$ 和 $v$，表示点 $u$ 和点 $v$ 之间存在一条边。

输出格式：
如果给定图是二分图，则输出 Yes，否则输出 No。

数据范围：
$1\le n,m\le 10^5$

输入样例：

4 4
1 3
1 4
2 3
2 4

输出样例：

Yes

代码实现：

这里采用DFS实现，其实也可以用BFS实现。

#include
#include

using namespace std;

const int N = 1e5 + 10; // 定义最大顶点数
int h[N], e[N], ne[N], idx; // 邻接表相关数组
int n, m; // n为顶点数，m为边数
int color[N]; // 记录顶点颜色，初始化为0，表示未访问过

// 添加边的函数
void add(int a, int b)
{
    e[idx] = b; // 边的终点
    ne[idx] = h[a]; // 与顶点a相连的上一条边的编号
    h[a] = idx++; // h[a]存储与顶点a相连的最后一条边的编号
}

// 深度优先搜索函数，用于判断图是否为二分图
bool dfs(int u, int c)
{
    color[u] = c; // 将顶点u标记为颜色c
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i]; // 与顶点u相连的顶点j
        if (!color[j]) // 如果顶点j未被标记
		{
		 	// 标记与顶点u相反的颜色，递归调用dfs函数
			// 如果递归返回false，说明不是二分图，直接返回false
			if (!dfs(j, 3 - c)) return false;
		}
		// 如果顶点j已被标记，并且颜色与顶点u相同，说明不是二分图，返回false
        else if (color[j] == c) return false; 
    }
    return true; // 如果顶点u及其邻接点都符合二分图定义，则返回true
}

int main()
{
    cin.tie(0);
    ios::sync_with_stdio(false);
    memset(h, -1, sizeof h); // 初始化邻接表数组为-1
    cin >> n >> m; // 输入顶点数和边数
    for (int i = 0; i < m; ++i)
    {
        int a, b;
        cin >> a >> b; // 输入边的两个顶点
        add(a, b), add(b, a); // 添加无向边
    }
    bool flag = true; // 初始化标志位为true
    for (int i = 1; i <= n; ++i)
    {
        if (!color[i] && !dfs(i, 1)) // 对每个未被标记的顶点进行dfs染色，如果返回false，则不是二分图
        {
            flag = false; // 将标志位设为false
            break; // 直接跳出循环
        }
    }
    if (flag) // 如果标志位为true，输出"Yes"
        cout << "Yes" << endl;
    else // 否则输出"No"
        cout << "No" << endl;
    return 0;
}

tip：
妙用 $3-c$ 来表示与当前顶点相反的颜色。

扩展问题：

关押罪犯

匈牙利算法（计算二分图的最大匹配）

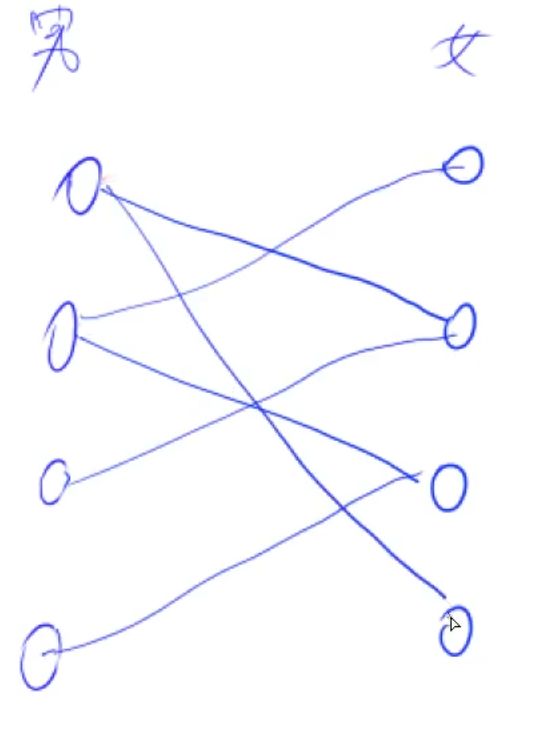
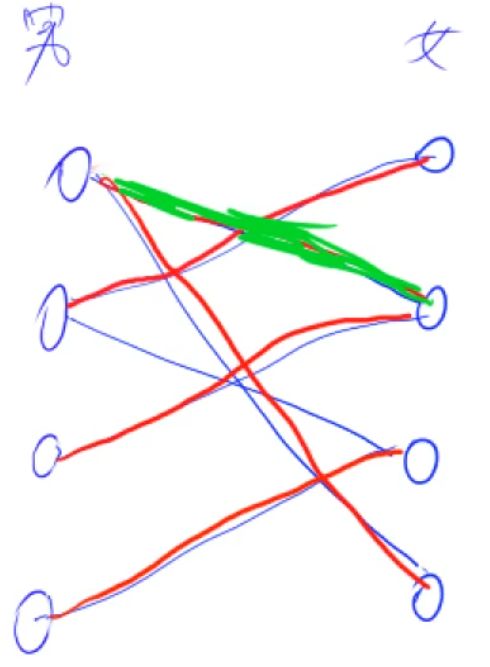
匈牙利算法（Hungarian algorithm）是用于解决二分图最大匹配问题。其基本思想是通过寻找增广路径来不断增加匹配的边数，直到无法找到新的增广路径为止。

二分图的匹配

• 二分图的匹配：给定一个二分图 $G$，在 $G$ 的一个子图 $M$ 中，$M$ 的边集 $E$ 中的任意两条边都不依附于同一个顶点，则称 $M$ 是一个匹配。

• 二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。

匹配前：

匹配后：

算法步骤

下面是匈牙利算法的具体步骤：

1. 初始化：将所有顶点的匹配状态置为未匹配（$match$ 数组初始化为 $0$）。

2. 遍历左侧顶点：对于二分图的每个左侧顶点i，开始寻找增广路径。

• 将当前左侧顶点i的状态数组 $st$ 初始化为 $false$，用于标记增广路径中的顶点是否已经被访问。
• 对当前左侧顶点 $i$，尝试在其邻接表中寻找一个未匹配的右侧顶点 $j$（如果存在），或者找到一个能够与右侧顶点 $j$ 存在增广路径的未匹配顶点。
• 若找到这样的顶点 $j$，则将右侧顶点 $j$ 与左侧顶点i进行匹配（即将 $match[j]$ 设置为 $i$），表示找到一条增广路径。

3. 增加匹配数：在找到一条增广路径后，将匹配数 $res$ 加 $1$。

4. 重复步骤 $2$ 和步骤 $3$：重复执行上述步骤，直到无法找到新的增广路径为止。

5. 输出结果：最终匹配的边数 $res$ 即为二分图的最大匹配数。

算法应用

二分图的最大匹配

题目描述：
给定一个二分图，其中左半部包含 $n_1$ 个点（编号 $1\sim n_1$），右半部包含 $n_2$ 个点（编号 $1\sim n_2$），二分图共包含 $m$ 条边。

数据保证任意一条边的两个端点都不可能在同一部分中。

请你求出二分图的最大匹配数。

输入格式：
第一行包含三个整数 $n_1、n_2和m$。

接下来 $m$ 行，每行包含两个整数 $u$ 和 $v$，表示左半部点集中的点 $u$ 和右半部点集中的点 $v$ 之间存在一条边。

输出格式：
输出一个整数，表示二分图的最大匹配数。

数据范围：
$1\le n_1,n_2\le 500$
$1\le u\le n_1$
$1\le v\le n_2$
$1\le m\le 10^5$

输入样例：

2 2 4
1 1
1 2
2 1
2 2

输出样例：

2

代码实现：

#define _CRT_SECURE_NO_WARNINGS

#include
#include

using namespace std;

const int N = 510, M = 1e5 + 10;
int n1, n2, m;
bool st[N]; // 数组用于在DFS过程中标记访问过的节点
int h[N], e[M], ne[M], idx, match[N]; // 图的表示和匹配数组

void add(int a, int b)
{
    e[idx] = b; // 将节点 'b' 添加到节点 'a' 的邻接表中
    ne[idx] = h[a]; // 更新节点 'a' 的邻接表指针
    h[a] = idx++; // 更新节点 'a' 的邻接表头指针，idx自增表示下一个插入的边的索引
}

bool find(int x)
{
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i]; // j为节点x的邻居节点
        if (st[j]) continue; // 如果节点j已经被访问过，则跳过
        st[j] = true; // 标记节点j为已访问
        if (match[j] == 0 || find(match[j])) // 如果节点j未匹配或者节点j的匹配节点能够寻找到增广路径
        {
            match[j] = x; // 将节点x匹配给节点j
            return true; // 返回成功匹配
        }
    }
    return false; // 无法找到增广路径，返回失败
}

int main()
{
    cin.tie(0); // 提高输入输出的效率
    ios::sync_with_stdio(false); // 关闭输入输出流的同步
    int res = 0; // 最大匹配数初始化为0
    memset(h, -1, sizeof h); // 初始化邻接表头指针为-1
    cin >> n1 >> n2 >> m; // 输入图的节点数和边数
    for (int i = 0; i < m; ++i)
    {
        int a, b;
        cin >> a >> b; // 输入图的边
        add(a, b); // 将边添加到邻接表中
    }
    for (int i = 1; i <= n1; ++i)
    {
        memset(st, false, sizeof st); // 每次匹配前都要将访问数组st重置为false
        if (find(i)) res++; // 尝试将节点i匹配，如果匹配成功，则最大匹配数加1
    }
    cout << res << endl; // 输出最大匹配数
}

扩展问题：

棋盘覆盖