- 智驾技术全链条解析
TrustZone_
智驾智驾
智驾技术全链条解析(2025年最新版)智驾技术涵盖从环境感知到车辆控制的完整闭环,涉及硬件、算法、数据与系统集成等多个领域。以下结合行业最新进展(截至2025年3月)进行深度拆解:一、感知技术:汽车的“感官系统”多传感器融合架构•核心传感器类型:◦激光雷达:华为ADS3.0采用200米探测距离的激光雷达,实现高精度三维建模,但成本较高(约2500元/颗);◦毫米波雷达:用于穿透雨雾探测,比亚迪天神
- 代码随想录算法营Day62 | 寻宝(Prim算法,kruskal算法)
寂枫zero
算法python
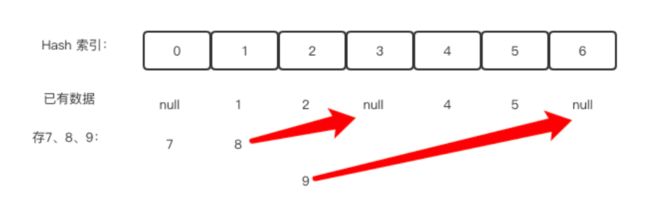
寻宝(Prim算法,kruskal算法)在世界的某个区域,有一些分散的神秘岛屿,每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路,方便运输。不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将所有岛屿联通起来(注意:这是一个无向图)。给定一张地图,其中包括了所有的岛屿,以及它们之间的距离。以最小化公路建设长度,确保可以链接到所有岛屿。最小生成树P
- 考研复习之记忆方法
herosunly
考名校研究生经验分享考研
大家好,我是herosunly。985院校硕士毕业,现担任算法研究员一职,热衷于大模型算法的研究与应用。曾担任百度千帆大模型比赛、BPAA算法大赛评委,编写微软OpenAI考试认证指导手册。曾获得阿里云天池比赛第一名,CCF比赛第二名,科大讯飞比赛第三名。授权多项发明专利。对机器学习和深度学习拥有自己独到的见解。曾经辅导过若干个非计算机专业的学生进入到算法行业就业。希望和大家一起成长进步。
- 数据挖掘|关联分析与Apriori算法详解
皖山文武
数据挖掘商务智能数据挖掘关联分析Apriori算法机器学习
数据挖掘|关联分析与Apriori算法1.关联分析2.关联规则相关概念2.1项目2.2事务2.3项目集2.4频繁项目集2.5支持度2.6置信度2.7提升度2.8强关联规则2.9关联规则的分类3.Apriori算法3.1Apriori算法的Python实现3.2基于mlxtend库的Apriori算法的Python实现1.关联分析关联规则分析(Association-rulesAnalysis)是数
- OPPO机器学习算法岗(AI智能体)内推
飞300
人工智能业界资讯
专注于以端设备为中心的AI智能体研究与应用,研究方向包括但不限于智能体与多智能体框架、大模型推理与规划、大模型工具使用等。1、负责大模型驱动的AI智能体框架的实现、评估与优化,并参与构建产品原型;2、设计微调方案、适配算法和调优工程方案,结合智能体应用,实现最佳效果与性能;3、跟踪与研究AI智能体相关前沿技术,并针对大模型推理与规划、工具使用、结构化输出等提出创新性方案。推荐码:X3448036
- 跨领域算法安全优化与可解释实践
智能计算研究中心
其他
内容概要作为系统性研究框架,《跨领域算法安全优化与可解释实践》从算法研发的全生命周期切入,重点解决多领域交叉应用中的核心矛盾。通过整合联邦学习的分布式架构与量子计算的高效特性,构建兼顾隐私保护与运算效率的算法优化范式,同时引入动态可解释性分析技术,为医疗影像诊断、金融风险预测等高敏感场景提供决策透明度保障。在技术路径层面,研究聚焦特征工程的鲁棒性设计、超参数的自适应调优策略,以及生成对抗网络在数据
- 智能算法安全与跨领域创新实践
智能计算研究中心
其他
内容概要在智能算法快速渗透各行业的背景下,安全治理与技术创新已成为驱动跨领域应用的核心议题。当前研究重点围绕算法可解释性增强、动态风险评估及数据安全防护展开,通过融合联邦学习的分布式协作框架、量子计算的算力突破以及注意力机制的特征聚焦能力,构建起多模态技术融合的创新路径。在应用场景层面,医疗影像诊断、金融风险预测与自动驾驶系统等关键领域已形成算法效能与安全性的双重验证体系,其中超参数优化、特征工程
- 算力安全创新驱动未来趋势endofsentence
智能计算研究中心
其他
内容概要算力安全与技术创新正在重塑全球算力生态,其核心驱动力来自异构计算、边缘计算及量子计算等前沿技术的深度融合。当前算力架构正经历从集中式向分布式演进,通过异构加速芯片、动态资源调度算法及绿色能效优化,显著提升算力基础设施的可扩展性与可靠性。例如,异构计算通过CPU、GPU、FPGA的协同加速,使复杂模型训练效率提升40%以上。关键数据:根据IDC预测,到2025年全球智能算力需求将增长30倍,
- STM32实时时钟(RTC)代码深度解析 | 零基础入门STM32第三十九步
触角01010001
STM32stm32单片机嵌入式硬件
主题内容教学目的/扩展视频RTC时钟的使用重点课程RTC时钟的原理,电路原理分析,固件库分析,驱动程序分析。在超级终端上显示时钟。做可修改的超级终端显示RTC的项目。师从洋桃电子,杜洋老师文章目录一、RTC初始化流程分析1.1时钟与备份域配置1.2初始化检测机制二、时间处理核心算法2.1闰年判断算法2.2时间戳转换(Unix时间)三、时间读取与转换3.1读取计数器值3.2星期计算算法四、中断处理机
- 1.动手学习深度学习课程安排及深度学习数学基础
Unknown To Known
动手学习深度学习深度学习人工智能
视频资源B站:动手学习深度学习——李沐目录目标内容将学到什么1.N维数组样例2.访问2维数组元素3.数据操作4.线性代数5.矩阵计算6.自动求导目标介绍深度学习景点和最新模型LeNetAlexNetVGGResNetLSTMBERT…机器学习基础损失函数,目标函数,过拟合,优化实践使用pytorch实现介绍的知识点在真实数据上体验算法效果内容深度学习基础——线性神经网络,多层感知机卷积神经网络——
- Python实现链表反转:迭代与递归双解法详解
达不溜先生 ୧⍢⃝୨
python数据结构链表算法leetcode
目录一、问题描述二、核心代码实现2.1迭代法实现迭代法中的prev初始值是None的原因:关键步骤图解2.2递归法实现递归法中要设置head.next=None的原因递归过程拆解三、方法对比与选择建议一、问题描述链表反转是数据结构中的基础算法问题,常见于面试和算法题库(如LeetCode#206)。要求将单向链表的节点顺序完全倒置二、核心代码实现2.1迭代法实现时间复杂度:O(n)空间复杂度:O(
- H100架构解析与性能优化策略
智能计算研究中心
其他
内容概要NVIDIAH100GPU作为面向高性能计算与人工智能领域的旗舰级产品,其架构设计与优化策略在计算效率、显存带宽及并行任务处理等方面实现了显著突破。本文将从核心架构创新与典型场景调优两个维度展开:首先解析第三代TensorCore的稀疏计算加速机制、FP8混合精度支持特性及其对矩阵运算的优化效果;其次,针对显存子系统中HBM3堆栈布局、L2缓存分区策略以及数据预取算法的协同优化进行拆解;最
- Java快排算法详解
大梦谁先觉i
数据结构与算法算法java排序算法
快排算法底层基本思想:先取出数列中的第一个数作为基准数。将数列中比基准数大的数全部放在他的右边,比基准数小的数全部放在它的左边。然后在对左右两部分重复第二步,直到各个区间只有一个数。具体Java代码实现publicclassQuickSort{publicstaticvoidsort(int[]array,intlow,inthigh){if(low=benchmark){high--;}//比基
- 【排序算法】选择排序
啥也不会干的小码
排序算法排序算法算法c语言
一、定义:选择排序(Selectionsort)是一种简单直观的排序算法。第一次从待排序的数据(元素)中选出最小(或最大)的一个元素,存放在数组的起始位置,然后再从剩余的没有排序的元素中寻找到最小(大)元素,然后放到已排序的数组的末尾。以此类推,直到全部待排序的数据元素的个数为零。对于数据量大的排序就没啥用了,排的比较慢。二、原理:1、对于待排序的数组,我们从首元素开始,将首元素的下标用min记住
- 归并排序(二叉树的后续遍历思想和数组的双指针技巧)
冰火同学
力扣算法排序算法数据结构
这次归并排序就只讲思路了,代码实现放到下次刷题再做首先确认一下归并排序的时间复杂度是NlogN的时间复杂度。实现归并排序的算法,我认为有几个困难需要克服掉1、首先就是要明确归并排序的算法思想,就是二叉数据的后序遍历,就是先从中间分割成两个子数组,然后继续分,直到只剩下一个元素,那么此时就是有序的,这个和构造二叉树时的分解思想十分相似,把子问题全部解决,那问题也就都解决了,至于我们只关注其中一个节点
- 第 146 题「LRU缓存机制」(手撸LRU算法)
冰火同学
力扣缓存数据结构算法
首选用比较通俗的语言来讲一讲LRU算法,那手机内存来举例子,就是当内存超出了手机设置的内存后,就要删除了内存,那删除那部分内存呢,LRU算法就是提供一个策略来选择那些需要缓存需要被删除掉,就是谁隔得最远就删除掉谁。LRU算法的描述怎么描述呢,其实上述描述的就是LRU算法要实现的逻辑只不多是人能理解的活,那么如何从写代码的角度来说一下实现LRU算法的逻辑呢,这个时候就要通过基础的数据结构结合来讲LR
- C语言实现排序之选择排序算法
Seraphina_Lily
C语言排序算法排序算法c语言算法
1.代码#include#include#include//函数声明int*create_and_generate_random_array(intsize);voidprint_array(int*array,intsize);voidselection_sort(int*array,intsize);intgenerate_random_size();intmain(){intsize=gen
- 如何有效管理 JavaScript 中的内存:垃圾回收与最佳实践
名之以父
JavaScript前端安全javascript前端框架react.jsvue.js网络
“垃圾回收是现代编程语言的核心特性之一,它使得开发者可以专注于功能实现,而无需担心内存管理的细节。”——在JavaScript中,垃圾回收(GC)是一个自动化的内存管理过程,它帮助我们确保不再使用的内存得到释放。尽管JavaScript的垃圾回收机制非常强大,但如果对其原理和工作方式不够了解,也可能导致一些性能问题和内存泄漏。本文将深入探讨JavaScript中的垃圾回收机制、算法以及如何优化垃圾
- 卡尔曼滤波算法c语言stm32,卡尔曼滤波算法及C语言实现_源代码
weixin_39643255
卡尔曼滤波算法c语言stm32
a往南向北2019-01-1620:39:2011340收藏111分类专栏:C语言嵌入式文章标签:卡尔曼滤波C代码卡尔曼滤波理论很容易就可以在MATLAB软件环境下实现,但是,实际的硬件板子上还是需要C语言,当然可以自动代码生成,还有一种就是直接手动编写C语言。1.前言在google上搜索卡尔曼滤波,很容易找到以下这个帖子:http://blog.csdn.net/lanbing510/artic
- 《算法二》选择排序算法及它的时间复杂度
code 旭
算法选择排序算法算法选择排序时间复杂度
1.选择排序算法选择排序算法的时间复杂度为O(N^2)选择排序算法规则:1.指定位置的数和后面的数比较2.如果指定位置的数大,则两个数交换位置3.向后移动一个位置,和指定位置的数进行比较假设数组大小n,第一轮比较n-1次,最小的数排在了最前面第二轮比较,第一个数已经是最小不用比较,此轮比较n-2次,第二小的排在第二个位置。依次类推,最后一轮,一次比较,最后得出有序的数列1.1和冒泡排序算法相比选择
- K-means 算法核心原理
code 旭
AI人工智能学习算法kmeans机器学习
一、K-means算法核心原理1.算法目标将n个样本划分到k个簇中,使得每个样本到所属簇中心的距离平方和最小。2.数学公式目标函数(SSE,簇内平方误差):J=∑i=1k∑x∈Ci∥x−μi∥2J=\sum_{i=1}^k\sum_{x\inC_i}\|x-\mu_i\|^2J=i=1∑kx∈Ci∑∥x−μi∥2其中:CiC_iCi表示第iii个簇μi\mu_iμi表示第iii个簇的质心二、算法步
- XGBoost常见面试题(五)——模型对比
月亮月亮要去太阳
机器学习经验分享
XGBoost与GBDT的区别机器学习算法中GBDT和XGBOOST的区别有哪些?-知乎基分类器:传统GBDT以CART树作为基分类器,xgboost还支持线性分类器,这个时候xgboost相当于带L1和L2正则化项的逻辑斯蒂回归(分类问题)或者线性回归(回归问题)。导数:传统GBDT在优化时只用到一阶导数信息,xgboost则对代价函数进行了二阶泰勒展开,同时用到了一阶和二阶导数。同时xgboo
- 【算法】BFS(最短路径问题、拓扑排序)
秦jh_
算法算法数据结构c++
个人主页:秦jh_-CSDN博客系列专栏:https://blog.csdn.net/qinjh_/category_12862161.html?fromshare=blogcolumn&sharetype=blogcolumn&sharerId=12862161&sharerefer=PC&sharesource=qinjh_&sharefrom=from_link目录边权为1的最短路径问题多源
- MPU6050 卡尔曼滤波算法 四元数欧拉姿态解算 STM32 CubeMX HAL库 MDKkeil5 零基础移植
辛尘大海
算法stm32嵌入式硬件
文章目录一、在cubemx开启IIC并设置好对应的IIC引脚二、generatecode生成代码三、复制以下的全部代码新建分别保存放到IncSrc文件夹中1.MPU6050.h2.MPU6050.C四、如何使用总结一、在cubemx开启IIC并设置好对应的IIC引脚二、generatecode生成代码(记得生成单个c.h.文件)!!!!!!三、复制以下的全部代码新建分别保存放到IncSrc文件夹中
- 常用图像增强算法原理及 OpenCV C++ 实现
埃菲尔铁塔_CV算法
opencv计算机视觉人工智能c++算法机器学习
一、引言图像增强是数字图像处理中的一个重要分支,其目的是改善图像的视觉效果,突出图像中的重要信息,或者将图像转换为更适合人或机器分析处理的形式。在实际应用中,图像增强技术广泛应用于医学影像、遥感图像、安防监控等领域。本文将详细介绍常用的图像增强算法原理,并给出基于OpenCVC++库的实现代码。二、图像增强算法分类图像增强算法可以分为空间域增强和频域增强两大类。空间域增强是直接对图像的像素值进行操
- 算法与数据结构(回文数)
a_j58
数据结构
题目思路对于这个我的第一想法就是转换为字符串然后判断字符串是否为回文,它会消耗额外的地址空间。还有一种想法就是将数字反转并判断是否为回文,但可能需要处理数字溢出的问题。若要避免出现数字溢出的问题,我们可以只反转它的一半,若前半部分和后半部分相同,则说明它是一个回文数。如123321,我们将它的后半部分反转,得到123,它与前半部分相同,说明它是一个回文数。算法首先,我们可以先考虑到它的一些临界情况
- 垃圾收集算法与收集器
HBryce24
JVMjvm
在JVM中,垃圾收集(GarbageCollection,GC)算法的核心目标是自动回收无用对象的内存,同时尽量减少对应用性能的影响。以下是JVM中主要垃圾收集算法的原理、流程及实际应用场景的详细介绍:一、标记-清除算法(Mark-Sweep)原理标记阶段:从GCRoots(如栈引用、静态变量)出发,遍历对象图,标记所有存活对象。清除阶段:扫描堆内存,回收未被标记的对象所占用的内存(直接释放,不整
- 【二分算法】-- 三种二分模板总结
雨雨雨雨点子
算法算法java开发语言leetcode
文章目录1.特点2.学习中的侧重点2.1算法原理2.2模板2.2.1朴素二分模板(easy-->有局限)2.2.2查找左边界的二分模板2.2.3查找右边界的二分模板1.特点二分算法是最恶心,细节最多,最容易写出死循环的算法====但是,一旦掌握了之后,二分算法就是最简单的算法。其实并不是一定要二分,三分,四分也都可以,但是根据概率学中的求期望数学中可知,二分是效率最高的。如果是三分的话,我们就像是
- 卡尔曼滤波算法从理论到实践:在STM32中的嵌入式实现
DOMINICHZL
STM32算法stm32嵌入式硬件
摘要:卡尔曼滤波(KalmanFilter)是传感器数据融合领域的经典算法,在姿态解算、导航定位等嵌入式场景中广泛应用。本文将从公式推导、代码实现、参数调试三个维度深入解析卡尔曼滤波,并给出基于STM32硬件的完整工程案例。一、卡尔曼滤波核心思想1.1什么是卡尔曼滤波?卡尔曼滤波是一种最优递归估计算法,通过融合预测值(系统模型)与观测值(传感器数据),在噪声干扰环境下实现对系统状态的动态估计。其核
- 递推和递归_一文学会递归递推
HR刀姐
递推和递归
递归算法和递推算法无论是在ACM竞赛还是项目工程上都有着极为广泛的应用,但想要完全掌握两者的思想并不容易,对于刚刚接触编程的人来说更是这样,我在初次接触递归递推时就吃了很多的苦头,除了当时对编程语言不太熟悉之外,最大的原因就是难以理解其中的思想,本文将二者结合代码分别讲解,力求以"理论+实践"的方式使读者明白两种算法。一箭双雕,一文双递。一.递归和递推的区别学习递归递推的一个容易遇到的问题就是混淆
- 如何用ruby来写hadoop的mapreduce并生成jar包
wudixiaotie
mapreduce
ruby来写hadoop的mapreduce,我用的方法是rubydoop。怎么配置环境呢:
1.安装rvm:
不说了 网上有
2.安装ruby:
由于我以前是做ruby的,所以习惯性的先安装了ruby,起码调试起来比jruby快多了。
3.安装jruby:
rvm install jruby然后等待安
- java编程思想 -- 访问控制权限
百合不是茶
java访问控制权限单例模式
访问权限是java中一个比较中要的知识点,它规定者什么方法可以访问,什么不可以访问
一:包访问权限;
自定义包:
package com.wj.control;
//包
public class Demo {
//定义一个无参的方法
public void DemoPackage(){
System.out.println("调用
- [生物与医学]请审慎食用小龙虾
comsci
生物
现在的餐馆里面出售的小龙虾,有一些是在野外捕捉的,这些小龙虾身体里面可能带有某些病毒和细菌,人食用以后可能会导致一些疾病,严重的甚至会死亡.....
所以,参加聚餐的时候,最好不要点小龙虾...就吃养殖的猪肉,牛肉,羊肉和鱼,等动物蛋白质
- org.apache.jasper.JasperException: Unable to compile class for JSP:
商人shang
maven2.2jdk1.8
环境: jdk1.8 maven tomcat7-maven-plugin 2.0
原因: tomcat7-maven-plugin 2.0 不知吃 jdk 1.8,换成 tomcat7-maven-plugin 2.2就行,即
<plugin>
- 你的垃圾你处理掉了吗?GC
oloz
GC
前序:本人菜鸟,此文研究学习来自网络,各位牛牛多指教
1.垃圾收集算法的核心思想
Java语言建立了垃圾收集机制,用以跟踪正在使用的对象和发现并回收不再使用(引用)的对象。该机制可以有效防范动态内存分配中可能发生的两个危险:因内存垃圾过多而引发的内存耗尽,以及不恰当的内存释放所造成的内存非法引用。
垃圾收集算法的核心思想是:对虚拟机可用内存空间,即堆空间中的对象进行识别
- shiro 和 SESSSION
杨白白
shiro
shiro 在web项目里默认使用的是web容器提供的session,也就是说shiro使用的session是web容器产生的,并不是自己产生的,在用于非web环境时可用其他来源代替。在web工程启动的时候它就和容器绑定在了一起,这是通过web.xml里面的shiroFilter实现的。通过session.getSession()方法会在浏览器cokkice产生JESSIONID,当关闭浏览器,此
- 移动互联网终端 淘宝客如何实现盈利
小桔子
移動客戶端淘客淘寶App
2012年淘宝联盟平台为站长和淘宝客带来的分成收入突破30亿元,同比增长100%。而来自移动端的分成达1亿元,其中美丽说、蘑菇街、果库、口袋购物等App运营商分成近5000万元。 可以看出,虽然目前阶段PC端对于淘客而言仍旧是盈利的大头,但移动端已经呈现出爆发之势。而且这个势头将随着智能终端(手机,平板)的加速普及而更加迅猛
- wordpress小工具制作
aichenglong
wordpress小工具
wordpress 使用侧边栏的小工具,很方便调整页面结构
小工具的制作过程
1 在自己的主题文件中新建一个文件夹(如widget),在文件夹中创建一个php(AWP_posts-category.php)
小工具是一个类,想侧边栏一样,还得使用代码注册,他才可以再后台使用,基本的代码一层不变
<?php
class AWP_Post_Category extends WP_Wi
- JS微信分享
AILIKES
js
// 所有功能必须包含在 WeixinApi.ready 中进行
WeixinApi.ready(function(Api) {
// 微信分享的数据
var wxData = {
&nb
- 封装探讨
百合不是茶
JAVA面向对象 封装
//封装 属性 方法 将某些东西包装在一起,通过创建对象或使用静态的方法来调用,称为封装;封装其实就是有选择性地公开或隐藏某些信息,它解决了数据的安全性问题,增加代码的可读性和可维护性
在 Aname类中申明三个属性,将其封装在一个类中:通过对象来调用
例如 1:
//属性 将其设为私有
姓名 name 可以公开
- jquery radio/checkbox change事件不能触发的问题
bijian1013
JavaScriptjquery
我想让radio来控制当前我选择的是机动车还是特种车,如下所示:
<html>
<head>
<script src="http://ajax.googleapis.com/ajax/libs/jquery/1.7.1/jquery.min.js" type="text/javascript"><
- AngularJS中安全性措施
bijian1013
JavaScriptAngularJS安全性XSRFJSON漏洞
在使用web应用中,安全性是应该首要考虑的一个问题。AngularJS提供了一些辅助机制,用来防护来自两个常见攻击方向的网络攻击。
一.JSON漏洞
当使用一个GET请求获取JSON数组信息的时候(尤其是当这一信息非常敏感,
- [Maven学习笔记九]Maven发布web项目
bit1129
maven
基于Maven的web项目的标准项目结构
user-project
user-core
user-service
user-web
src
- 【Hive七】Hive用户自定义聚合函数(UDAF)
bit1129
hive
用户自定义聚合函数,用户提供的多个入参通过聚合计算(求和、求最大值、求最小值)得到一个聚合计算结果的函数。
问题:UDF也可以提供输入多个参数然后输出一个结果的运算,比如加法运算add(3,5),add这个UDF需要实现UDF的evaluate方法,那么UDF和UDAF的实质分别究竟是什么?
Double evaluate(Double a, Double b)
- 通过 nginx-lua 给 Nginx 增加 OAuth 支持
ronin47
前言:我们使用Nginx的Lua中间件建立了OAuth2认证和授权层。如果你也有此打算,阅读下面的文档,实现自动化并获得收益。SeatGeek 在过去几年中取得了发展,我们已经积累了不少针对各种任务的不同管理接口。我们通常为新的展示需求创建新模块,比如我们自己的博客、图表等。我们还定期开发内部工具来处理诸如部署、可视化操作及事件处理等事务。在处理这些事务中,我们使用了几个不同的接口来认证:
&n
- 利用tomcat-redis-session-manager做session同步时自定义类对象属性保存不上的解决方法
bsr1983
session
在利用tomcat-redis-session-manager做session同步时,遇到了在session保存一个自定义对象时,修改该对象中的某个属性,session未进行序列化,属性没有被存储到redis中。 在 tomcat-redis-session-manager的github上有如下说明: Session Change Tracking
As noted in the &qu
- 《代码大全》表驱动法-Table Driven Approach-1
bylijinnan
java算法
关于Table Driven Approach的一篇非常好的文章:
http://www.codeproject.com/Articles/42732/Table-driven-Approach
package com.ljn.base;
import java.util.Random;
public class TableDriven {
public
- Sybase封锁原理
chicony
Sybase
昨天在操作Sybase IQ12.7时意外操作造成了数据库表锁定,不能删除被锁定表数据也不能往其中写入数据。由于着急往该表抽入数据,因此立马着手解决该表的解锁问题。 无奈此前没有接触过Sybase IQ12.7这套数据库产品,加之当时已属于下班时间无法求助于支持人员支持,因此只有借助搜索引擎强大的
- java异常处理机制
CrazyMizzz
java
java异常关键字有以下几个,分别为 try catch final throw throws
他们的定义分别为
try: Opening exception-handling statement.
catch: Captures the exception.
finally: Runs its code before terminating
- hive 数据插入DML语法汇总
daizj
hiveDML数据插入
Hive的数据插入DML语法汇总1、Loading files into tables语法:1) LOAD DATA [LOCAL] INPATH 'filepath' [OVERWRITE] INTO TABLE tablename [PARTITION (partcol1=val1, partcol2=val2 ...)]解释:1)、上面命令执行环境为hive客户端环境下: hive>l
- 工厂设计模式
dcj3sjt126com
设计模式
使用设计模式是促进最佳实践和良好设计的好办法。设计模式可以提供针对常见的编程问题的灵活的解决方案。 工厂模式
工厂模式(Factory)允许你在代码执行时实例化对象。它之所以被称为工厂模式是因为它负责“生产”对象。工厂方法的参数是你要生成的对象对应的类名称。
Example #1 调用工厂方法(带参数)
<?phpclass Example{
- mysql字符串查找函数
dcj3sjt126com
mysql
FIND_IN_SET(str,strlist)
假如字符串str 在由N 子链组成的字符串列表strlist 中,则返回值的范围在1到 N 之间。一个字符串列表就是一个由一些被‘,’符号分开的自链组成的字符串。如果第一个参数是一个常数字符串,而第二个是type SET列,则 FIND_IN_SET() 函数被优化,使用比特计算。如果str不在strlist 或st
- jvm内存管理
easterfly
jvm
一、JVM堆内存的划分
分为年轻代和年老代。年轻代又分为三部分:一个eden,两个survivor。
工作过程是这样的:e区空间满了后,执行minor gc,存活下来的对象放入s0, 对s0仍会进行minor gc,存活下来的的对象放入s1中,对s1同样执行minor gc,依旧存活的对象就放入年老代中;
年老代满了之后会执行major gc,这个是stop the word模式,执行
- CentOS-6.3安装配置JDK-8
gengzg
centos
JAVA_HOME=/usr/java/jdk1.8.0_45
JRE_HOME=/usr/java/jdk1.8.0_45/jre
PATH=$PATH:$JAVA_HOME/bin:$JRE_HOME/bin
CLASSPATH=.:$JAVA_HOME/lib/dt.jar:$JAVA_HOME/lib/tools.jar:$JRE_HOME/lib
export JAVA_HOME
- 【转】关于web路径的获取方法
huangyc1210
Web路径
假定你的web application 名称为news,你在浏览器中输入请求路径: http://localhost:8080/news/main/list.jsp 则执行下面向行代码后打印出如下结果: 1、 System.out.println(request.getContextPath()); //可返回站点的根路径。也就是项
- php里获取第一个中文首字母并排序
远去的渡口
数据结构PHP
很久没来更新博客了,还是觉得工作需要多总结的好。今天来更新一个自己认为比较有成就的问题吧。 最近在做储值结算,需求里结算首页需要按门店的首字母A-Z排序。我的数据结构原本是这样的:
Array
(
[0] => Array
(
[sid] => 2885842
[recetcstoredpay] =&g
- java内部类
hm4123660
java内部类匿名内部类成员内部类方法内部类
在Java中,可以将一个类定义在另一个类里面或者一个方法里面,这样的类称为内部类。内部类仍然是一个独立的类,在编译之后内部类会被编译成独立的.class文件,但是前面冠以外部类的类名和$符号。内部类可以间接解决多继承问题,可以使用内部类继承一个类,外部类继承一个类,实现多继承。
&nb
- Caused by: java.lang.IncompatibleClassChangeError: class org.hibernate.cfg.Exten
zhb8015
maven pom.xml关于hibernate的配置和异常信息如下,查了好多资料,问题还是没有解决。只知道是包冲突,就是不知道是哪个包....遇到这个问题的分享下是怎么解决的。。
maven pom:
<dependency>
<groupId>org.hibernate</groupId>
<ar
- Spark 性能相关参数配置详解-任务调度篇
Stark_Summer
sparkcachecpu任务调度yarn
随着Spark的逐渐成熟完善, 越来越多的可配置参数被添加到Spark中来, 本文试图通过阐述这其中部分参数的工作原理和配置思路, 和大家一起探讨一下如何根据实际场合对Spark进行配置优化。
由于篇幅较长,所以在这里分篇组织,如果要看最新完整的网页版内容,可以戳这里:http://spark-config.readthedocs.org/,主要是便
- css3滤镜
wangkeheng
htmlcss
经常看到一些网站的底部有一些灰色的图标,鼠标移入的时候会变亮,开始以为是js操作src或者bg呢,搜索了一下,发现了一个更好的方法:通过css3的滤镜方法。
html代码:
<a href='' class='icon'><img src='utv.jpg' /></a>
css代码:
.icon{-webkit-filter: graysc