代码随想录算法训练营第二天| 19. 删除链表的倒数第 N 个结点， 02.07. 链表相交， 24. 两两交换链表中的节点， 142. 环形链表 II

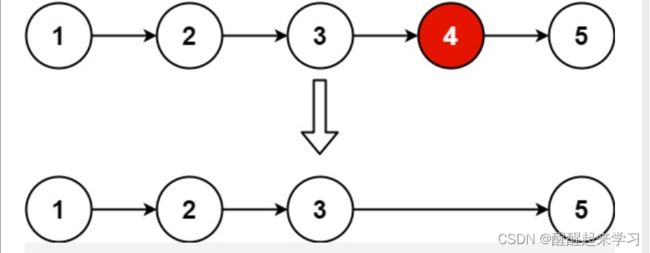
 19. 删除链表的倒数第 N 个结点

之前一直是用遍历两次链表的方法做，这次看到了新思路用 双指针解法

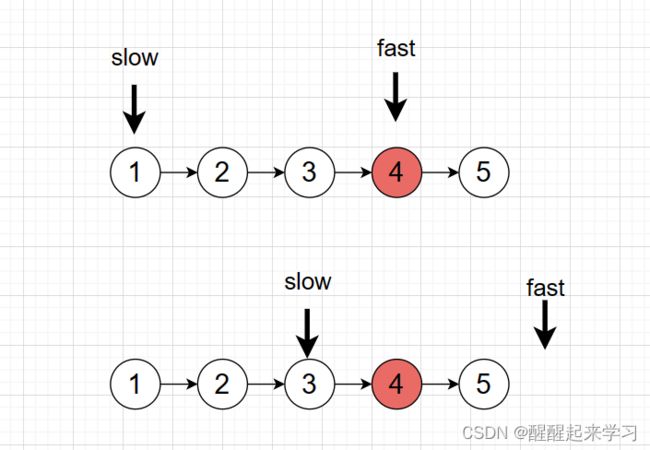
让fast和slow指针最初都指向哑节点dummy，然后要让fast节点走n+1次，使得fast节点指向要被删除的节点，这时候slow指针和fast指针同时出发，直到fast==null时，slow指针会刚好指向被删除节点的前一个节点

图示：

n=2 要删除的是倒数第2个节点

 

 

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode removeNthFromEnd(ListNode head, int n) {

        ListNode dummy=new ListNode(-1,head);
        ListNode fast=dummy;
        ListNode slow =dummy;

        for(int i=0;i<=n;i++){
            fast=fast.next;
        }
        //fast和slow同时移动
        while(fast!=null){
            fast=fast.next;
            slow=slow.next;
        }
        //slow指向要被删除节点的前一个
        slow.next=slow.next.next;
        return dummy.next;//考虑到【1】 n=1的情况，所以一开始我是返回的head，然后改成返回dummy.next

    }
}

  02.07. 链表相交

 真的很吃惊，看了卡哥的思路后代码一遍就AC了！

思路是，首先分析，把相交链表想象成两条链表，把两条链表的尾部对齐的话很容易看出相交的节点，因此我们先分别计算两条链表的长度，并得到长度差值，让长链表的指针先走完这个差值，然后再让长链表当前指针和短链表当前指针一起遍历，直到遇到共同的节点

图示：

 

 代码的思路：

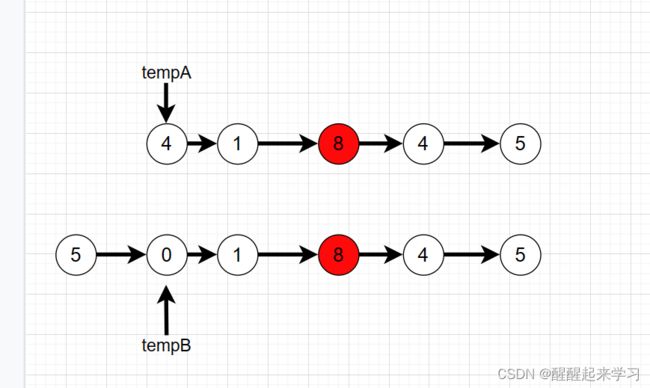
链表A节点数是5

链表B节点数是6

二者差是1，又由于链表B比较长，我们定义tempA和tempB分别指向链表A,B的头节点，让tempB先走完差值，然后再让tempA和tempB一起走

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode cur1=headA;
        int count1=0;
        ListNode cur2=headB;
        int count2=0;
        while(cur1!=null){
            count1++;
            cur1=cur1.next;
        }
         while(cur2!=null){
            count2++;
            cur2=cur2.next;
        }
        int cha=Math.abs(count2-count1);
        if(count1-count2>=0){
            //
            for(int i=0;i

封装成方法更简洁

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
        ListNode cur1=headA;
        int count1=0;
        ListNode cur2=headB;
        int count2=0;
        //1.分别计算两个链表的长度
        while(cur1!=null){
            count1++;
            cur1=cur1.next;
        }
         while(cur2!=null){
            count2++;
            cur2=cur2.next;
        }
        //2.求出长度的差值并取绝对值
        int cha=Math.abs(count2-count1);
        if(count1-count2>=0){
           return judge(headA,headB,cha);
        }
        else{
           return judge(headB,headA,cha);
        }
      
        
    }
    public ListNode judge(ListNode headA,ListNode headB,int cha){
            for(int i=0;i

 24. 两两交换链表中的节点

开始不会写，看的题解，用的递归的思路，非常简洁，学习了  

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode swapPairs(ListNode head) {

         //递归
        if(head==null||head.next==null){return head;}//不加head.next==null的话下面"head.next.next"会报错
        ListNode t1=head.next;
        ListNode t2=head.next.next;
        t1.next=head;
        head.next=swapPairs(t2);
        return t1;
    }
}

 142. 环形链表 II

之前刷过1次，这次看一遍卡哥的思路就写出来了，下面自己推导一遍

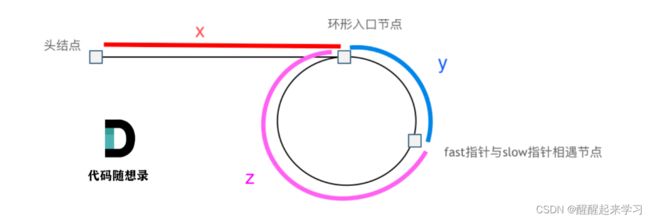
如何找到环入口呢？

假设从头结点到环形入口节点 的节点数为x。 环形入口节点到 fast指针与slow指针相遇节点 节点数为y。 从相遇节点 再到环形入口节点节点数为 z。

 fast指针每次走两步，slow指针每次走一步

在环内相遇时：

fast的路程：x+y+(y+z)n  

其中n是fast指针在环内绕了n圈

slow的路程：x+y

根据速度-时间法则: x+y+(y+z)n=2(x+y)  

注意我们的目的是得到x，因此可以解得x=(y+z)(n-1)+z

当n=1时，x=z

ok，我只能推导到这里了。。

这就意味着，从头结点出发一个指针，从相遇节点 也出发一个指针，这两个指针每次只走一个节点， 那么当这两个指针相遇的时候就是 环形入口的节点。

那么 n如果大于1是什么情况呢，就是fast指针在环形转n圈之后才遇到 slow指针。

在相遇节点处，定义一个指针index1，在头结点处定一个指针index2。

其实这种情况和n为1的时候效果是一样的，一样可以通过这个方法找到环形的入口节点，只不过，index1 指针在环里 多转了(n-1)圈，然后再遇到index2，相遇点依然是环形的入口节点。

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) {
 *         val = x;
 *         next = null;
 *     }
 * }
 */
public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode fast=head;
        ListNode slow=head;
        if(head==null||head.next==null){return null;}
        while(fast.next!=null&&fast.next.next!=null){
            fast=fast.next.next;
            slow=slow.next;
            if(fast==slow){//在环中相遇
               ListNode cur=head;
               while(cur!=fast){
                   cur=cur.next;
                   fast=fast.next;
               }
               return cur;
            }
        }
     return null;
    }
}