机器学习之KNN、Python实现

一、前言

knn虽然基础，但是应用还是很多的。性价比不错。
在知乎上看到一句话：
KNN是新来的小弟选一个山头， K-means是群龙无首小弟们选举出新的山头（可以多个）

很形象的解释了，knn与k-means的区别

重要元素：
KNN算法有K值的选择、距离计算和决策方法等三个基本要素

二、KNN

（1）简介

1. KNN是一种基于实例的无参学习算法，通过计算新数据与训练集中所有样本之间的距离，并选取k个最近邻来进行分类或回归预测。在分类问题中，KNN算法采用多数投票的方法进行决策；在回归问题中，KNN算法采用平均值法进行预测。
2. 因此，KNN算法的目标是将新数据点分配给与其距离最近的训练数据点所属的类别或者预测其对应的数值，而不是最小化某个损失函数。也正因为如此，KNN算法适用于许多非线性和非参数化的问题，但也具有一定的局限性，例如在处理高维度数据时，KNN算法的时间和空间复杂度会随着样本数量的增加呈指数级增长，导致效率低下。

（2）思想: “近朱者赤近墨者黑”

KNN（K-Nearest Neighbors）算法的核心思想是基于样本间的距离来进行分类或回归。在分类问题中，给定一个新的样本，KNN算法会在训练数据集中找到k个距离该样本最近的样本，然后根据这k个样本所属类别的多数投票结果来确定该样本的类别。在回归问题中，KNN算法同样寻找k个距离该样本最近的样本，然后取它们的平均值作为该样本的回归预测结果

（3）算法实现流程

1. 准备数据：将已知类别的数据集按照一定规则进行划分，通常把其中的一部分作为训练集，另一部分作为测试集。

2. 计算距离：对于每一个待分类的样本，计算它与训练集中所有样本之间的距离。通常使用欧氏距离（Euclidean Distance）或曼哈顿距离（Manhattan Distance）等度量方式来进行距离计算。
   常见的欧式距离：

d(p, q) = sqrt((p1 - q1)^2 + (p2 - q2)^2 + ... + (pn - qn)^2)

其中，p1, p2, …, pn和q1, q2, …, qn分别表示向量p和向量q在各自的第1个维度到第n个维度上的坐标值。sqrt表示计算平方根。

3. 选择K值：根据预设的K值，选取距离该样本最近的K个样本。

4. 进行预测：根据K个最近的样本的类别，通过投票决定该样本所属的类别。通常采用多数表决（Majority Vote）的方式，即选择出现次数最多的类别作为预测结果。

5. 评估模型：使用测试集对模型进行评估，通常使用错误率（Error Rate）或精确度（Accuracy）等指标来衡量模型的性能。

（4）k值得选定

k值的选定，是一件很重要的事情，直接影响了模型的表现能力。

1. k值得作用

k值是KNN算法的一个超参数，K的含义即参考”邻居“标签值的个数。 有个反直觉的现象，K取值较小时，相当于我们在较小的领域内训练样本对实例进行预测。这时，算法的近似误差（Approximate Error）会比较小，因为只有与输入实例相近的训练样本才会对预测结果起作用。预测的结果对紧邻点十分敏感，容易导致过拟合；同理：K取值较大时，模型复杂度低，训练误差会增大，泛化能力有一定的提高，容易欠拟合。

2. 交叉验证选取 k值

在KNN算法中，选择合适的K值非常重要，直接影响到模型的分类准确率。为了确定最优的K值，可以使用交叉验证（Cross Validation）方法进行。常用的交叉验证方法有K折交叉验证和留一法交叉验证。

以K折交叉验证为例，具体实现步骤如下：

1. 将原始数据集分成K个子集，将其中一个子集作为测试集，剩余的K-1个子集作为训练集。

2. 在K-1个训练集上运用KNN算法，得到不同的分类模型，并将这些模型对测试集进行分类。

3. 计算每个模型的分类准确率，并计算它们的平均值作为该K值下的分类准确率。

4. 重复以上步骤，直到尝试完所有可能的K值为止。

5. 根据得到的分类准确率，选择最优的K值作为KNN算法的参数。

需要注意的是，在实际应用中，一般将样本量较小的数据集划分为更少的折数，而将样本量较大的数据集划分为更多的折数，以提高模型的泛化能力和准确性。同时，还需要考虑到模型的计算效率和时间成本等因素，选择一个合适的K值。

三、KNN基于sklearn实现

基于上面的算法步骤流程进行逐步实现

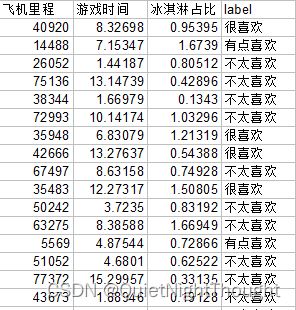
（1.）准备数据

使用约会数据进行简单处理

（2.）k值得选择

这里我们使用 交叉验证方法：代码如下

#todo 加载数据
    data = pd.read_csv('knnData.csv')
    x = data.iloc[:,0:3]
    y = data.iloc[:,-1:]
    print(x)
    k_accuracy = []
    for i in range(1,31):
        knn = KNeighborsClassifier(n_neighbors=i)
        socres = cross_val_score(knn,x,y,cv=10,scoring='accuracy')
        k_accuracy.append(socres.mean())
        '''
        在进行交叉验证时，我们会对模型在不同的“折”上的表现进行评估，并计算所有“折”的得分的平均值。因此，这里使用scores.mean()将模型在每个“折”上的得分求平均，得到一个k值对应的平均准确率。
        cross_val_score函数默认返回每个“折”上的得分（即一个长度为10的数组），而这里我们需要的是该k值下的平均准确率，因此使用scores.mean()将数组中的得分求平均。
        具体来说，scores.mean()计算的是模型在10折交叉验证中所有“折”上得分的平均值，作为当前k值的平均准确率。  
        '''
    plt.plot(range(1,31),k_accuracy)
    plt.xlabel('Value of k for KNN')
    plt.ylabel('Cross-Validated Accuracy')
    plt.show()

看下效果展示：

可以看到，当k值为18的时候，我们的模型准确率最高
因此，k值我们就设定为18

（3.）进行模型搭建

选定好 k值后就开始进行模型搭建：

data = pd.read_csv('knnData.csv')
#进行特征值的选择
x = data.iloc[:,0:3]
y = data.iloc[:,-1:]
# 创建色彩图
cmap_light = ListedColormap(['orange', 'cyan', 'cornflowerblue'])
cmap_bold = ListedColormap(['darkorange', 'c', 'darkblue'])

X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.3)

'''
weights（权重）：最普遍的 KNN 算法无论距离如何，权重都一样，但有时候我们想搞点特殊化，比如距离更近的点让它更加重要。这时候就需要 weight 这个参数了，这个参数有三个可选参数的值，决定了如何分配权重。参数选项如下：
• ‘uniform’：不管远近权重都一样，就是最普通的 KNN 算法的形式。
• ‘distance’：权重和距离成反比，距离预测目标越近具有越高的权重。
• 自定义函数：自定义一个函数，根据输入的坐标值返回对应的权重，达到自定义权重的目的。
'''
#todo 分别在两种权重情况下进行对比

for weights in ["uniform","distance"]:

    #todo 第一步：创建knn分类器
    knn = neighbors.KNeighborsClassifier(n_neighbors = 18,weights=weights)
    knn.fit(X_train,y_train)

    #todo 第二步: 用测试集进行预测，并计算准确率
    y_pred = knn.predict(X_test)
    print(y_pred)
    # accuracy = np.mean(y_pred == y_test)

（4.）模型使用

检验下模型效果：

  #使用模型预测新的数据点
    X_new = np.array([[38344, 3.0, 0.1343], [3436, 3.0, 4.0], [7, 9.0, 6.0]])
    y_new = knn.predict(X_new)  # 预测新的数据点类别

    print(f"New data point {X_new[0]} belongs to class {[y_new[0]]}")
    print(f"New data point {X_new[1]} belongs to class {[y_new[1]]}")
    print(f"New data point {X_new[2]} belongs to class {[y_new[2]]}")

打印结果：

哈哈效果一般啊：

（5.）模型问题

1. 对于数据的第一列没用进行归一化操作，可以看到两种不同
2. 对于标签值没有进行数字化处理
3. 对于大型数据集处理起来太慢

四、针对上面问题进行knn封装

（1）数据处理

目的：对数据进行归一化是为了将不同特征的数值范围统一到相同的区间内，以避免某些特征对模型训练的影响过大。
好处：归一化可以提高模型的收敛速度和精度，并且有助于提高算法的鲁棒性和泛化能力
方法：常见的归一化方法包括最小-最大归一化、均值方差归一化等。

均值方差归一化

均值方差归一化（Mean-Variance Normalization）是一种数据归一化方法，也称为标准化（Standardization）。它通过对原始数据进行线性变换，使其均值为0，标准差为1。

具体而言，假设原始数据集为$X=x_1,x_2,...,x_n$，其中$x_i$是第$i$个样本的特征向量。则均值方差归一化的公式如下：

$$\bar{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$$

$$\sigma =\sqrt{\frac{1}{n}\sum _{i=1}^n(x_i-\bar{x}{)}^2}$$

$$x_i^{\prime }=\frac{x_i-\bar{x}}{\sigma }$$

其中，$\bar{x}$表示样本特征的平均值，$\sigma$表示样本特征的标准差。对每一个特征都执行以上操作，即可实现均值方差归一化。

均值方差归一化可以使得数据分布更加接近标准正态分布，从而提高模型的准确性和稳定性。同时，该方法也可以避免由于不同特征之间数量级不同而导致的误差或偏差。常见的机器学习算法如神经网络、支持向量机等都需要进行均值方差归一化处理

代码可以使用：

import numpy as np

def mean_variance_normalize(X):
    """
    均值方差归一化
    :param X: ndarray类型的数据集
    :return: 归一化后的数据集
    """
    X_norm = (X - np.mean(X, axis=0)) / np.std(X, axis=0)
    return X_norm

其中，X是一个ndarray类型的数据集，np.mean(X, axis=0)和np.std(X, axis=0)分别计算了每个特征的均值和标准差。在代码中，我们使用了numpy库来进行矩阵运算，从而提高计算效率。
例如：

#创建一个3*4的数据集
X = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])

最小-最大归一化

最小-最大归一化（Min-Max Normalization），又称离差标准化，是一种常用的数据归一化方法。它将原始数据通过线性变换映射到[0,1]区间内。

具体而言，假设原始数据集为$X=x_1,x_2,...,x_n$，其中$x_i$是第$i$个样本的特征向量。则最小-最大归一化的公式如下：

$$x_i^{\prime }=\frac{x_i-\min (X)}{\max (X)-\min (X)}$$

其中，$\min (X)$表示样本特征的最小值，$\max (X)$表示样本特征的最大值。对每一个特征都执行以上操作，即可实现最小-最大归一化。

最小-最大归一化可以使得数据分布更加均匀，避免了由于不同特征之间数量级不同而导致的误差或偏差。该方法适用于数据的最大值和最小值已知的情况，并且对异常值敏感。在某些需要保留数据分布形态的场景下，最小-最大归一化不太适用，比如一些机器学习算法要求输入数据应该服从正态分布。

代码实现：

def min_max_normalize(X):
    """
    最小-最大归一化
    :param X: ndarray类型的数据集
    :return: 归一化后的数据集
    """
    X_norm = (X - np.min(X, axis=0)) / (np.max(X, axis=0) - np.min(X, axis=0))
    return X_norm

其中，X是一个ndarray类型的数据集，np.min(X, axis=0)和np.max(X, axis=0)分别计算了每个特征的最小值和最大值。在代码中，我们使用了numpy库来进行矩阵运算，从而提高计算效率

数据处理

（2）不掉包实现完整代码

（3）KNN使用KD树加速

五、完整代码

（1）调包实现完整代码

使用sklearn进行knn实现

（2）不掉包实现完整代码

六、KNN的优缺点

七、参考文献

[1].https://zhuanlan.zhihu.com/p/45453761
[2].https://www.zhihu.com/question/40456656
[3].https://zhuanlan.zhihu.com/p/122195108
[4].https://blog.csdn.net/codedz/article/details/108862498
[5].https://blog.csdn.net/c406495762/article/details/75172850