正规文法、正规表达式、有限自动机及其之间的转换（笔记）

The Equivalent Transforming among RG, RE and FA

正规文法

A Grammar G is a quadruple (四元组):G = (V_N, V_T, S, P )

Where,

• V_N is a finite set of nonterminals.
• V_T is a finite set of terminals.
• S is the start symbol, S$\in$ V_N.
• P is a finite set of productions (产生式).

Regular Grammar (RG) (正规文法):

α∈V_N and β ∈V_T∪V_TV_N

正规表达式

Regular Expression:

Regular expressions over ∑ are defined as :

1. ε and $\varphi$ are RE’s, denoting the sets {ε} and Φ , respectively ;
2. Any a $\in$∑ , a is an RE, denoting the set { a };
3. If a and b are RE’s, denoting the sets A and B respectively, then a b , a | b, and a* are RE’s, denoting the sets AB, AUB and A* respectively;
4. Nothing is an RE unless it follows from 1 to 3 finite times.

有限自动机

确定的有限自动机

Deterministic Finite Automata:

A Deterministic Finite Automaton (DFA) is a quintuple (五元组)

M = (S, ∑ , f, s₀ , Z),

where

• S is a finite set of states;
• ∑ is the set of input symbols;
• f : S×∑ →S, the transition function;
• s₀ $\in$S, the initial state;
• Z $\subseteq$ S, the set of final states.

非确定有限自动机

Nondeterministic Finite Automata:

An Nondeterministic Finite Automata (NFA) is also a quintuple

M = ( S, ∑ , f, s₀ , Z),

where:

• S is a finite set of states;
• ∑ is the set of input symbols;
• f : S×∑* →ρ(S), the transition function;
• s₀$\in$S, the initial state;
• Z $\subseteq$S, the set of final states.

Difference between DFA & NFA

The definitions of transition functions of DFA and NFA are different:

​ DFA f: S×∑ →S

​ NFA f: S×∑* →ρ(S)

That means: a state of DFA has a unique next state and can not transit without input, but a state of NFA may have more than one next states and can transit without input.

正规表达式转换为正规文法

Transforming RE to RG

Let r be an RE on∑. Construct G = (V_N, V_T, S, P):

1. Initialization: V_T＝∑; P = {S → r}; V_N ={S};

2. For any production in P, rewrite it as follows:

   ⑴ A → x*y => A → xA |y.

   ⑵ A→x | y => A → x | y;

   ⑶A → xy => A → xB B → y; V_N = V_N ∪{B};

   ⑷A→(x | y)B =>A → xB | yB; V_N = V_N ∪{B};

   where x and y be RE’s, B be a new nonterminal.

3. Repeat step 2 until each rule has one termianal.

样例

Transform a(a | d)* to RG

V_T＝{a, b}; P = {S → a(a | d)* }; V_N ={S};

S → a(a | d)* => S → aA A → (a | d)*

A → (a | d)* => A → (a | d)A |ε

A → (a | d)A => A → aA | dA

Finally we get the regular grammar G is

({S, A}, {a, b}, S, {S→ aA A→ aA|dA|ε})

正规文法转换为正规表达式

Transforming RG to RE

1. Transform RG to a group of equations by replacing → and | as = and +, respectively.
2. For equations X = aY + a and Y = b, we replace Y by b, and get X = ab + a.
3. If there is an equation X=rX + t, we have the solution X = r*t;
4. Repeat step 2 and 3, until the solution S=r is got. Then r is the corresponding RE.

样例

Consider the grammar G:S → aS | aA A → bB B → aB | a

• Transform the rules into a group of equations:

  S = aS + aA (1)

  A = bB (2)

  B = aB + a (3)

• For equation 3 we have: B = a*a;

• For equation 2 we have: A = ba*a;

• For equation 1 we have: S = aS + aba*a;

• Finally we have: S = a*aba*a;

正规文法转换为有限自动机

Transforming RG to FA

G = (V_N, V_T, S, P) is a right linear grammar, there is an FA M such that L(M) = L(G).

Let M = (Q, ∑, f, s₀ , {Z}), where

∑= V_T; Q = V_N∪{Z}; Z$\notin$ V_N; s₀= S;

For $\forall$ A→tB∈P, t∈V_T∪{e}, A, B∈V_N, then f(A, t) = B;

For $\forall$ A→t∈P, A∈V_N, t∈V_T∪{ε}, then f(A, t) = Z.

样例

Given G＝({A,B,C,D},{0,1},f,A,P),

P = {A → 0 | 0B | 1D B → 0D | 1C

​ C → 0 | 0B| 1D D → 0D | 1D }

• Construct M = (Q,∑,f,A,{Z}):
• Q={A,B,C,D,Z}, ∑ = {0, 1},
• f(A, 0)=B, f(A, 0)=Z, f(A, 1)=D,
• f(B, 0)=D, f(B, 1)=C,
• f(C, 0)=B, f(C, 0)=Z, f(C, 1)=D,
• f(D, 0)=D, f(D, 1)=D.

有限自动机转换为正规文法

Transforming FA to RG

M=(Q, ∑, f, s₀ , F) is a DFA, there is a right linear grammar G such that L(M) = L(G).

Let G = (V_N, V_T, S, P), where

V_T = ∑; V_N = Q; S = s₀;

For $\forall$ t∈V_T, $\forall$ A, B∈V_N, if f(A, t) = B

then If B ∈F then A →tB | t∈P

​ else A→tB∈P;

样例

Given M＝({0,1},{A,B,C,D},f,A,{B})

• Construc G = (V_N,V_T, A, P),

• V_N = {A, B, C, D},

• V_T = {0, 1},

• P = { A → 0B | 0 | 1D

  ​ B → 0D | 1C

  ​ C → 0B | 0 | 1D D → 0D | 1D }

正规表达式转换为有限自动机

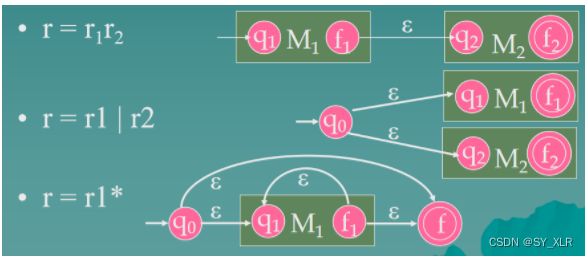
Transforming RE to FA

Given an RE r, there is an FA M, such that L(M) = L®.

• Basis: |r| = 1.
• We prove it by induction on the length of r.

Assume that for any RE r1 and r2, if |r1| < k and |r2| < k, they have their NFA M1 and M2.

• For any RE r, |r| = k, we have:

Initialization: set up two state X and Y, such as:

Repeat dividing the RE r on the arcs according to the following rules (1) to (3):

Until each arc labeled by a symbol.

样例

有限自动机转换为正规表达式

Transforming FA to RE

Initialization: Add two state : X , Y. X is the unique initial state and Y is the unique final state

Repeat linking the RE r on the arcs according to the following rules (1) to (3):

样例