看完必会的 python DEAP遗传算法库讲解+实战（中级）

喜欢的话请关注我们的微信公众号~《 你好世界炼丹师》。

• 公众号主要讲统计学，数据科学，机器学习，深度学习，以及一些参加Kaggle竞赛的经验。
• 公众号内容建议作为课后的一些相关知识的补充，饭后甜点。
• 此外，为了不过多打扰，公众号每周推送一次，每次4~6篇精选文章。

微信搜索公众号：你好世界炼丹师。期待您的关注。

---

TSP问题

之前用遗传算法解决了：多项式求极大值的问题。这个问题实在是太简单了，现在我们来处理一下更困难的问题——TSP旅行商问题

问题描述

• TSP旅行商问题，traveling Salesman problem
  -

• 如果旅行商从A地到B地的花费与B地到A地的花费相等，我们称之为对称旅行商问题（Symmetric Travelinig Salesman Problem（STSP））

• 反之就是非对称旅行商问题ATSP

• TSP问题的一个特殊性在于它必然存在可以找到的最优解（通过穷举法一定能在时间内找到该最优解），但是在计算复杂度方面它是一个经典的NP-hard问题。因而快速有效寻找TSP的最优解仍然是个有吸引力的问题。

• 在实际应用方面，它可以被视为物流调度，交通规划，芯片布线优化等等问题的抽象简化。

代码精讲

def genCity(n,LB=100,Ub=999):
    np.random.seed(42)
    return np.random.randint(low = Lb,high = Ub,size(n,2))

运行结果：

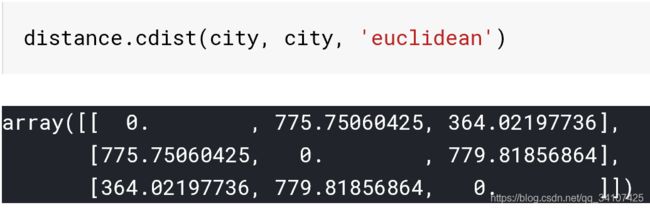
def cityDistance(cities):
    return distance.cdist(cities,cities,'euclidean')

运行结果：

def completeRoute(individual):
    return individual + [individual[0]]

这个completeRoute函数是用来表示：最后旅行商还要回到出发，也就是第一个城市的。
要记住给出来的这个方法，不是最优解，针对TSP问题，有很多很多种方法，之后我会专门写一个博文来讲解TSP问题

觉得博文有用的话，点个赞呗

整体代码（方便复制）

## 环境设置
import matplotlib.pyplot as plt
import numpy as np
%matplotlib inline
from scipy.spatial import distance
from deap import creator, base, tools, algorithms
import random

params = {
    'font.family': 'serif',
    'figure.figsize': [4.0, 3.0],
    'figure.dpi': 300,
    'savefig.dpi': 300,
    'font.size': 12,
    'legend.fontsize': 'small'
}
plt.rcParams.update(params)
#--------------------------------
## 定义TSP中的基本元素

# 用[n,2]的np.array存储城市坐标；每行存储一个城市
def genCity(n, Lb = 100 ,Ub = 999):
    # 生成城市坐标
    # 输入：n -- 需要生成的城市数量
    # 输出: nx2 np array 每行是一个城市的[X,Y]坐标
    np.random.seed(42) # 保证结果的可复现性
    return np.random.randint(low = Lb, high = Ub, size=(n,2))

# 计算并存储城市距离矩阵
def cityDistance(cities):
    # 生成城市距离矩阵 distMat[A,B] = distMat[B,A]表示城市A，B之间距离
    # 输入：cities -- [n,2] np array， 表示城市坐标
    # 输出：nxn np array， 存储城市两两之间的距离
    return distance.cdist(cities, cities, 'euclidean')

def completeRoute(individual):
    # 序列编码时，缺少最后一段回到原点的线段
    return individual + [individual[0]] # 不要用append
    
# 计算给定路线的长度
def routeDistance(route):
    # 输入：
    #      route -- 一条路线，一个sequence
    # 输出：routeDist -- scalar，路线的长度
    if route[0] != route[-1]:
        route = completeRoute(route)
    routeDist = 0
    for i,j in zip(route[0::],route[1::]):
        routeDist += cityDist[i,j] # 这里直接从cityDist变量中取值了，其实并不是很安全的写法，单纯偷懒了
    return (routeDist), # 注意DEAP要求评价函数返回一个元组

# 路径可视化
def plotTour(tour, cities, style = 'bo-'):
    if len(tour)>1000: plt.figure(figsize = (15,10))
    start = tour[0:1]
    for i,j in zip(tour[0::], tour[1::]):
        plt.plot([cities[i,0],cities[j,0]], [cities[i,1],cities[j,1]], style)
    plt.plot(cities[start,0],cities[start,1],'rD')
    plt.axis('scaled')
    plt.axis('off')
    
#--------------------------------
## 设计GA算法
nCities = 30
cities = genCity(nCities) # 随机生成nCities个城市坐标

# 问题定义
creator.create('FitnessMin', base.Fitness, weights=(-1.0,)) # 最小化问题
creator.create('Individual', list, fitness=creator.FitnessMin)

# 定义个体编码
toolbox = base.Toolbox()
toolbox.register('indices', random.sample, range(nCities), nCities) # 创建序列
toolbox.register('individual', tools.initIterate, creator.Individual, toolbox.indices)

# 生成族群
N_POP = 100
toolbox.register('population', tools.initRepeat, list, toolbox.individual)
pop = toolbox.population(N_POP)

# 注册所需工具
cityDist = cityDistance(cities)
toolbox.register('evaluate', routeDistance)
toolbox.register('select', tools.selTournament, tournsize = 2)
toolbox.register('mate', tools.cxOrdered)
toolbox.register('mutate', tools.mutShuffleIndexes, indpb = 0.2)

# 数据记录
stats = tools.Statistics(key=lambda ind: ind.fitness.values)
stats.register('avg', np.mean)
stats.register('min', np.min)

# 调用内置的进化算法
resultPop, logbook = algorithms.eaSimple(pop, toolbox, cxpb = 0.5, mutpb = 0.2, ngen = 200, stats = stats, verbose = True)

结果展示(不重要)

gen	nevals	avg    	min    
0  	100   	14176.2	11493.3
1  	64    	13910.9	11978.5
2  	57    	13541  	10887.5
3  	62    	13412.6	11239.2
4  	57    	13216.1	10838.4
5  	52    	12978  	10946.4
6  	69    	12869.9	10835.5
7  	53    	12758  	11159.4
8  	60    	12583.8	11159.4
9  	53    	12650.3	11159.4
10 	62    	12552.8	10144.1
11 	64    	12515.9	10144.1
12 	57    	12362.6	10144.1
13 	63    	11992  	10144.1
14 	66    	11884  	10144.1
15 	53    	11796.8	10144.1
16 	57    	11776.6	10144.1
17 	51    	11746.5	10144.1
18 	48    	11537.4	10144.1
19 	59    	11437.6	10144.1
20 	58    	11234  	10144.1
21 	57    	11000.2	10083.2
22 	56    	11078.9	9630.29
23 	72    	10949.4	9580.21
24 	64    	11049.6	9518.98
25 	67    	10902.3	9453.88
26 	62    	10668.6	9453.88
27 	73    	10742.1	9404.84
28 	59    	10794.2	9107.71
29 	64    	10441.8	9107.71
30 	61    	10436.8	9107.71
31 	58    	10601.1	9107.71
32 	58    	10575.8	9107.71
33 	57    	10638.7	9107.71
34 	63    	10602.3	9107.71
35 	63    	10520.9	9100.74
36 	70    	10647.6	8601.04
37 	69    	10613.3	8601.04
38 	64    	10361.7	8601.04
39 	67    	10315  	8601.04
40 	66    	10533.4	8601.04
41 	60    	10305.4	8601.04
42 	65    	10413.1	8601.04
43 	53    	10147.9	8023.66
44 	61    	9946.89	8111.77
45 	66    	10206  	8414.1 
46 	60    	10322.8	8414.1 
47 	47    	10175  	8414.1 
48 	60    	10112.6	8277.71
49 	67    	10158.7	8414.1 
50 	58    	9868.8 	8414.1 
51 	53    	9914.54	8414.1 
52 	67    	10175.3	8244.9 
53 	63    	9668.28	7754.85
54 	56    	9698.52	8229.29
55 	52    	9800.86	8139.39
56 	60    	9852.75	8079.22
57 	63    	9720.71	7907.92
58 	46    	9371.5 	7907.92
59 	78    	9840.35	7907.92
60 	60    	9786.13	7907.92
61 	58    	9611.86	7690.89
62 	57    	9620.83	7571.99
63 	58    	9602.33	7571.99
64 	65    	9710.81	7690.89
65 	57    	9721.93	7690.89
66 	55    	9532.58	7597.36
67 	66    	9726.2 	7714.35
68 	54    	9606.91	7714.35
69 	60    	9694.29	7714.35
70 	57    	9506.47	7286.83
71 	59    	9606.73	7286.83
72 	49    	9542.94	7286.83
73 	56    	9515.44	7286.83
74 	63    	9650.51	7286.83
75 	63    	9520.09	7286.83
76 	68    	9594.92	7286.83
77 	54    	9540.16	7286.83
78 	53    	9176.14	7279.77
79 	57    	9009.16	7286.83
80 	53    	9147.02	7286.83
81 	70    	9256.52	7286.83
82 	62    	9488.51	7366.65
83 	59    	9608.51	7346.74
84 	70    	9749.23	7346.74
85 	64    	9782.13	7274.49
86 	69    	9534.5 	7429.7 
87 	65    	9658.88	7316.42
88 	59    	9453.71	7316.42
89 	55    	9235.11	7316.42
90 	58    	9385.07	7447.42
91 	63    	9310.27	7443.17
92 	61    	9653.86	7397.92
93 	62    	9433.39	7227.34
94 	60    	9377.12	7227.34
95 	69    	9246.4 	7227.34
96 	63    	9355.57	7227.34
97 	53    	9305.01	7101.48
98 	68    	9295.37	7101.48
99 	69    	9665.86	7101.48
100	54    	9414.28	7101.48
101	58    	9155.82	7101.48
102	47    	9126.21	7101.48
103	56    	9044.02	7101.48
104	65    	9155.81	7101.48
105	53    	9026.01	7101.48
106	65    	9015.49	7101.48
107	53    	8863.79	7202.31
108	60    	9144.37	7222   
109	65    	8718.15	7148.14
110	61    	8601.87	7148.14
111	60    	8672.55	7114.1 
112	60    	8477.34	6912.14
113	70    	8395.44	6912.14
114	54    	8521.13	6912.14
115	54    	8417.96	6861.39
116	64    	8545.9 	6861.39
117	58    	8766.21	6912.14
118	66    	8887.49	6903.63
119	67    	9013.49	6912.14
120	63    	8664.06	6976.26
121	59    	8823.91	6934.69
122	65    	8717.36	6902.27
123	61    	8651.38	6902.27
124	59    	8782.75	6934.69
125	69    	8785.51	6655.75
126	64    	8377.19	6655.75
127	64    	8556.06	6655.75
128	67    	8392.15	6686.51
129	62    	8600.26	6686.51
130	65    	8784.4 	6686.51
131	63    	9243.02	6686.51
132	62    	9145.37	6665.55
133	59    	8683.87	6665.55
134	55    	8666.97	6343.75
135	51    	8738.7 	6442.21
136	64    	8720.62	6742.48
137	63    	9024.09	6359.37
138	58    	8891.69	6359.37
139	51    	8463.8 	6468.51
140	60    	8285.75	6468.51
141	49    	8393.2 	6468.51
142	68    	8436.04	6348.44
143	61    	8541.49	6348.44
144	68    	8579.33	6348.44
145	49    	8198.65	6183.56
146	65    	8382.85	6183.56
147	50    	8132.53	6183.56
148	62    	8617.13	6183.56
149	54    	8389.52	6183.56
150	58    	8251.35	6183.56
151	47    	8209.13	6183.56
152	64    	8274.1 	6183.56
153	62    	8439.32	6183.56
154	60    	8411.04	6183.56
155	58    	8281.42	6017.12
156	65    	8382.98	6017.12
157	67    	8668.16	6017.12
158	57    	8337.28	6017.12
159	50    	7883.74	6017.12
160	71    	8589.04	6017.12
161	55    	8107.54	6017.12
162	48    	7643.62	6017.12
163	71    	7879.85	6017.12
164	56    	7815.24	5889.87
165	58    	7985.76	6017.12
166	67    	8255.71	5923.56
167	59    	7882.04	5923.56
168	57    	8067.33	6017.12
169	56    	8383.83	5923.56
170	58    	8251.27	6017.12
171	53    	7677.3 	6017.12
172	48    	7769.81	6017.12
173	60    	8220.91	6017.12
174	60    	7938.42	5971.98
175	59    	7686.54	5971.98
176	62    	7856.47	5912.91
177	55    	8111.19	5912.91
178	65    	7818.76	5912.91
179	62    	8043.08	5912.91
180	61    	7949.82	5912.91
181	63    	8281.78	5912.91
182	60    	8377.56	5912.91
183	76    	8506.39	5912.91
184	45    	8017.97	5912.91
185	65    	8571.77	5699.04
186	56    	8243.96	5699.04
187	57    	8299.26	5699.04
188	64    	7988.19	5699.04
189	52    	7762   	5699.04
190	55    	7980.38	5699.04
191	52    	7704.22	5699.04
192	57    	7763.54	5597.01
193	62    	8239.91	5699.04
194	46    	8091.76	5699.04
195	60    	7915.62	5699.04
196	60    	8099.47	5699.04
197	62    	7898.96	5699.04
198	60    	7979.38	6011.46
199	64    	8236.56	5752.69
200	65    	8273.31	5752.69