GAN-FID计算
import os
import numpy as np
import torch
import time
from scipy import linalg # For numpy FID
from pathlib import Path
from PIL import Image
import models.models as models
from utils.fid_folder.inception import InceptionV3
import matplotlib.pyplot as plt
# --------------------------------------------------------------------------#
# This code is an adapted version of https://github.com/mseitzer/pytorch-fid
# --------------------------------------------------------------------------#
class fid_pytorch():
def __init__(self, opt, dataloader_val):
self.opt = opt
self.dims = 2048
block_idx = InceptionV3.BLOCK_INDEX_BY_DIM[self.dims]
self.model_inc = InceptionV3([block_idx])
if opt.gpu_ids != "-1":
self.model_inc.cuda()
self.val_dataloader = dataloader_val
self.m1, self.s1 = self.compute_statistics_of_val_path(dataloader_val)
self.best_fid = 99999999
self.path_to_save = os.path.join(self.opt.checkpoints_dir, self.opt.name, "FID")
Path(self.path_to_save).mkdir(parents=True, exist_ok=True)
def compute_statistics_of_val_path(self, dataloader_val):
print("--- Now computing Inception activations for real set ---")
pool = self.accumulate_inception_activations()
mu, sigma = torch.mean(pool, 0), torch_cov(pool, rowvar=False)
print("--- Finished FID stats for real set ---")
return mu, sigma
def accumulate_inception_activations(self):
pool, logits, labels = [], [], []
self.model_inc.eval()
with torch.no_grad():
for i, data_i in enumerate(self.val_dataloader):
image = data_i["image"]
if self.opt.gpu_ids != "-1":
image = image.cuda()
image = (image + 1) / 2
pool_val = self.model_inc(image.float())[0][:, :, 0, 0]
pool += [pool_val]
return torch.cat(pool, 0)
def compute_fid_with_valid_path(self, netG, netEMA):
pool, logits, labels = [], [], []
self.model_inc.eval()
netG.eval()
if not self.opt.no_EMA:
netEMA.eval()
with torch.no_grad():
for i, data_i in enumerate(self.val_dataloader):
image, label = models.preprocess_input(self.opt, data_i)
if self.opt.no_EMA:
generated = netG(label)
else:
generated = netEMA(label)
generated = (generated + 1) / 2
pool_val = self.model_inc(generated.float())[0][:, :, 0, 0]
pool += [pool_val]
pool = torch.cat(pool, 0)
mu, sigma = torch.mean(pool, 0), torch_cov(pool, rowvar=False)
answer = self.numpy_calculate_frechet_distance(self.m1, self.s1, mu, sigma)
netG.train()
if not self.opt.no_EMA:
netEMA.train()
return answer
def numpy_calculate_frechet_distance(self, mu1, sigma1, mu2, sigma2, eps=1e-6):
"""Numpy implementation of the Frechet Distance.
Taken from https://github.com/bioinf-jku/TTUR
The Frechet distance between two multivariate Gaussians X_1 ~ N(mu_1, C_1)
and X_2 ~ N(mu_2, C_2) is
d^2 = ||mu_1 - mu_2||^2 + Tr(C_1 + C_2 - 2*sqrt(C_1*C_2)).
Stable version by Dougal J. Sutherland.
Params:
-- mu1 : Numpy array containing the activations of a layer of the
inception net (like returned by the function 'get_predictions')
for generated samples.
-- mu2 : The sample mean over activations, precalculated on an
representive data set.
-- sigma1: The covariance matrix over activations for generated samples.
-- sigma2: The covariance matrix over activations, precalculated on an
representive data set.
Returns:
-- : The Frechet Distance.
"""
mu1, sigma1, mu2, sigma2 = mu1.detach().cpu().numpy(), sigma1.detach().cpu().numpy(), mu2.detach().cpu().numpy(), sigma2.detach().cpu().numpy()
mu1 = np.atleast_1d(mu1)
mu2 = np.atleast_1d(mu2)
sigma1 = np.atleast_2d(sigma1)
sigma2 = np.atleast_2d(sigma2)
assert mu1.shape == mu2.shape, \
'Training and test mean vectors have different lengths'
assert sigma1.shape == sigma2.shape, \
'Training and test covariances have different dimensions'
diff = mu1 - mu2
# Product might be almost singular
covmean, _ = linalg.sqrtm(sigma1.dot(sigma2), disp=False)
if not np.isfinite(covmean).all():
msg = ('fid calculation produces singular product; '
'adding %s to diagonal of cov estimates') % eps
print(msg)
offset = np.eye(sigma1.shape[0]) * eps
covmean = linalg.sqrtm((sigma1 + offset).dot(sigma2 + offset))
# Numerical error might give slight imaginary component
if np.iscomplexobj(covmean):
#print('wat')
if not np.allclose(np.diagonal(covmean).imag, 0, atol=1e-3):
m = np.max(np.abs(covmean.imag))
#print('Imaginary component {}'.format(m))
covmean = covmean.real
tr_covmean = np.trace(covmean)
out = diff.dot(diff) + np.trace(sigma1) + np.trace(sigma2) - 2 * tr_covmean
return out
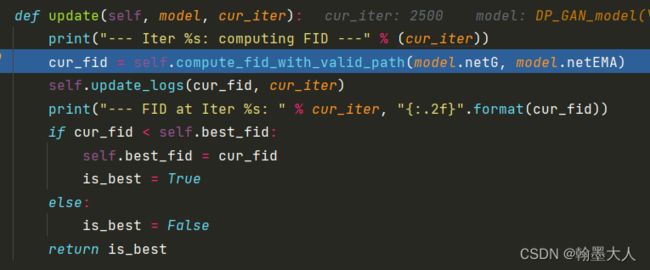
def update(self, model, cur_iter):
print("--- Iter %s: computing FID ---" % (cur_iter))
cur_fid = self.compute_fid_with_valid_path(model.netG, model.netEMA)
self.update_logs(cur_fid, cur_iter)
print("--- FID at Iter %s: " % cur_iter, "{:.2f}".format(cur_fid))
if cur_fid < self.best_fid:
self.best_fid = cur_fid
is_best = True
else:
is_best = False
return is_best
def update_logs(self, cur_fid, epoch):
try :
np_file = np.load(self.path_to_save + "/fid_log.npy")
first = list(np_file[0, :])
sercon = list(np_file[1, :])
first.append(epoch)
sercon.append(cur_fid)
np_file = [first, sercon]
except:
np_file = [[epoch], [cur_fid]]
np.save(self.path_to_save + "/fid_log.npy", np_file)
np_file = np.array(np_file)
plt.figure()
plt.plot(np_file[0, :], np_file[1, :])
plt.grid(b=True, which='major', color='#666666', linestyle='--')
plt.minorticks_on()
plt.grid(b=True, which='minor', color='#999999', linestyle='--', alpha=0.2)
plt.savefig(self.path_to_save + "/plot_fid", dpi=600)
plt.close()
def torch_cov(m, rowvar=False):
'''Estimate a covariance matrix given data.
Covariance indicates the level to which two variables vary together.
If we examine N-dimensional samples, `X = [x_1, x_2, ... x_N]^T`,
then the covariance matrix element `C_{ij}` is the covariance of
`x_i` and `x_j`. The element `C_{ii}` is the variance of `x_i`.
Args:
m: A 1-D or 2-D array containing multiple variables and observations.
Each row of `m` represents a variable, and each column a single
observation of all those variables.
rowvar: If `rowvar` is True, then each row represents a
variable, with observations in the columns. Otherwise, the
relationship is transposed: each column represents a variable,
while the rows contain observations.
Returns:
The covariance matrix of the variables.
'''
if m.dim() > 2:
raise ValueError('m has more than 2 dimensions')
if m.dim() < 2:
m = m.view(1, -1)
if not rowvar and m.size(0) != 1:
m = m.t()
# m = m.type(torch.double) # uncomment this line if desired
fact = 1.0 / (m.size(1) - 1)
m -= torch.mean(m, dim=1, keepdim=True)
mt = m.t() # if complex: mt = m.t().conj()
return fact * m.matmul(mt).squeeze()
FID作用:

FID计算公式:
计算公式

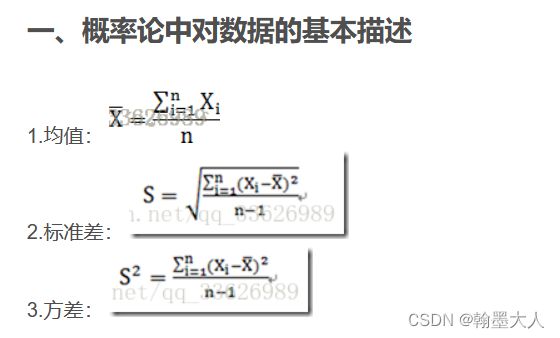
分三步首先求图片的特征均值,接着求图片的协方差矩阵,最后求迹。
1:如何求特征均值:

使用inception-v3可以求特征。
2:如何求协方差矩阵?
协方差矩阵是由协方差和方差组成的。矩阵对角元素是方差,其余元素是协方差。
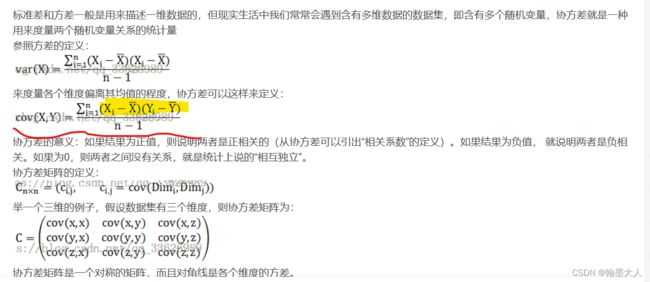
3:矩阵的迹就是对角元素相加。
代码:
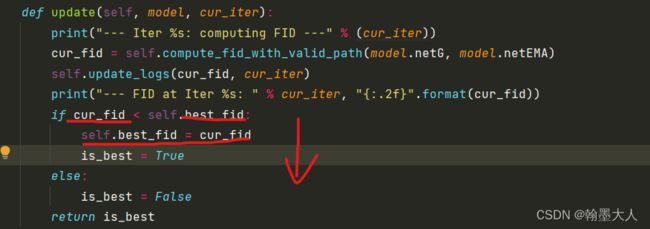
最重要的就是计算FID,因为FID越小越好,所以当前的FID小于最好的best_FID,那么best_FID就等于当前的FID。
在compute_fid_with_valid_path内部:

将标签输入到生成器中产生RGB图,将生成的RGB图输入到inceptionv3中:
inception参数由block_index决定,根据字典知block_index=3。
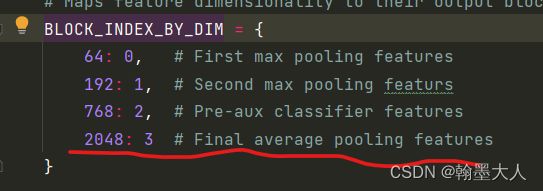

在InceptionV3内部:
首先将输入下采样到(299,299)大小。
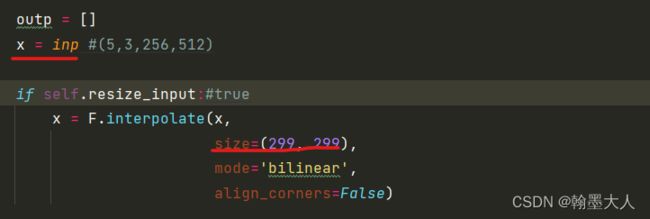
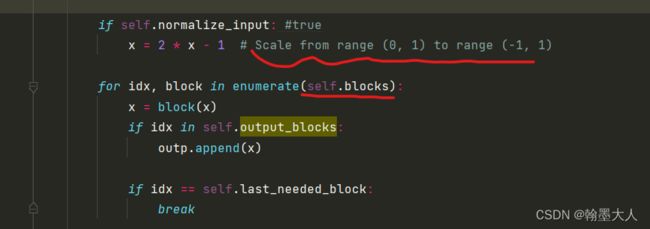
接着输入遍历block:
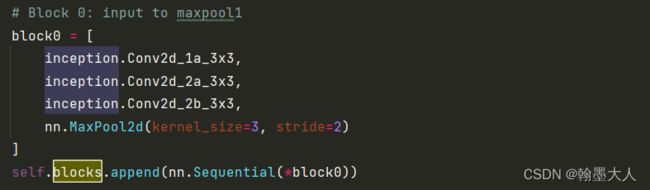
向modulist里面添加block0:
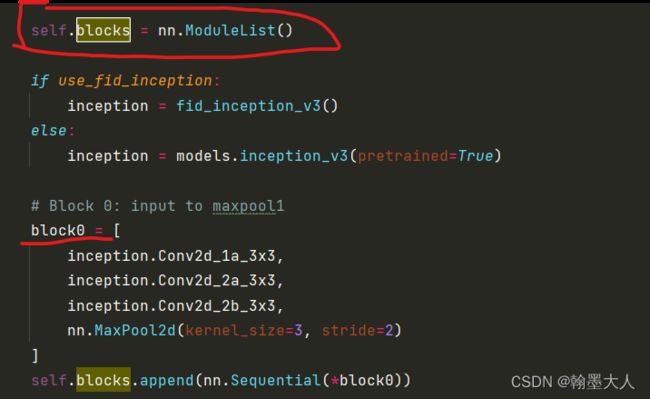
blcok由三个卷积组成,将输入图片下采样两倍,然后输出通道变为64,即(5,64,128,256),最后经过一个池化大小变为(5,64,64,128).卷积就是由一个卷积,一个BN,一个Relu组成。
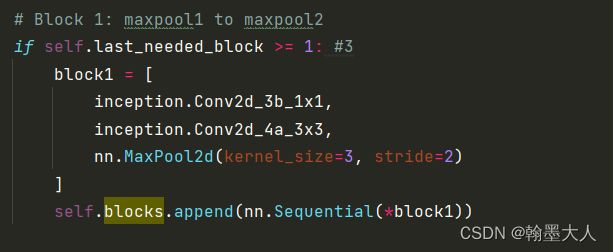
接着添加block1:
![]()
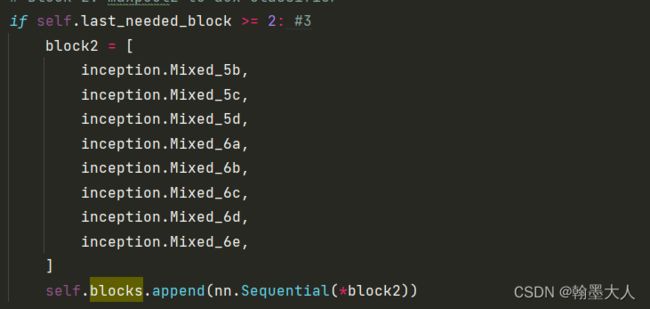
3:添加block2:
4:添加block3,则block里面有四个sequential。
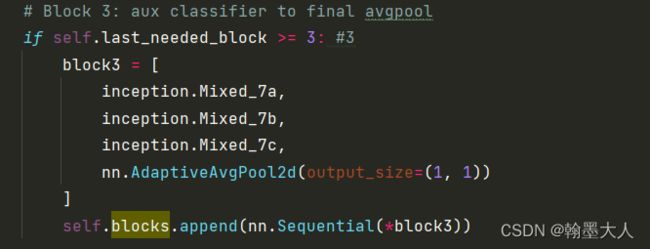
将x输入到inceptionv3,其中将idx等于3的输出添加到outp列表,即x完整经过inception的输出,然后跳出循环。最终输出为(5,2048).
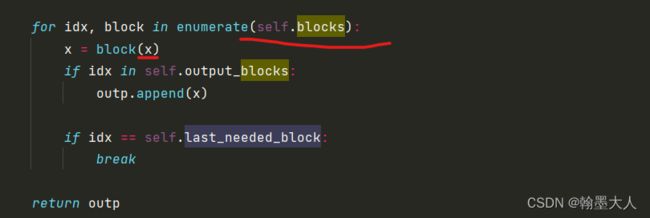
将验证集所有图片经过inceptionv3的结果添加到列表中,一共执行100次循环。
将列表数据按照通道维度拼接起来:(500,2048),对500张验证图片,每一张图片都有2048个概率输出。
接着mu等于沿着batch维度求所有图片的均值,sigma求协方差。则mu=[2048].
方差:
def torch_cov(m, rowvar=False):
'''Estimate a covariance matrix given data.
Covariance indicates the level to which two variables vary together.
If we examine N-dimensional samples, `X = [x_1, x_2, ... x_N]^T`,
then the covariance matrix element `C_{ij}` is the covariance of
`x_i` and `x_j`. The element `C_{ii}` is the variance of `x_i`.
Args:
m: A 1-D or 2-D array containing multiple variables and observations.
Each row of `m` represents a variable, and each column a single
observation of all those variables.
rowvar: If `rowvar` is True, then each row represents a
variable, with observations in the columns. Otherwise, the
relationship is transposed: each column represents a variable,
while the rows contain observations.
Returns:
The covariance matrix of the variables.
'''
if m.dim() > 2:
raise ValueError('m has more than 2 dimensions')
if m.dim() < 2:
m = m.view(1, -1)
if not rowvar and m.size(0) != 1:
m = m.t()
# m = m.type(torch.double) # uncomment this line if desired
fact = 1.0 / (m.size(1) - 1)
m -= torch.mean(m, dim=1, keepdim=True)
mt = m.t() # if complex: mt = m.t().conj()
return fact * m.matmul(mt).squeeze()
首先将m进行转置。m变为(2048,500)。
接着求fact=1/(500-1)对应于方差公式中的分母。接着m = m- torch.mean(m,dim=1)对应于方差分子括号里的x减去x的均值。m大小为(2048,500),torch.mean(m,dim=1)对应大小为(2048,1),两个相减,将(2048,1)广播到(2048,500)。
最后将m转置过来变为(500,2048)
最后fact乘以m*mt,其中m是(m-m.mean),mt是m转置,相当于m乘以m转置。求和符号包含其中,对应公式:

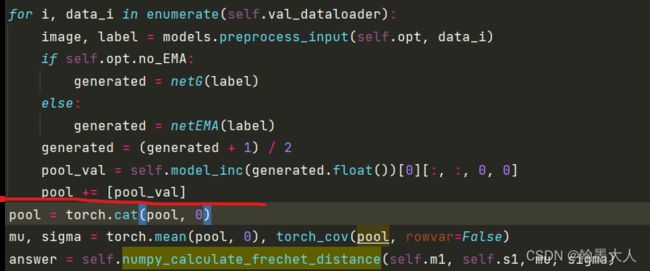
计算完mu,sigma就该计算self.m1和self.s1了。
![]()

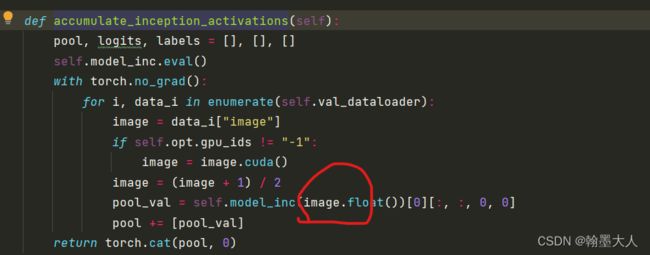
与之前不同的是这是inception输入的是image而不再是生成的图片了。但是操作和之前生成图片是一致的。
将之前的四个输出进行FID计算:
def numpy_calculate_frechet_distance(self, mu1, sigma1, mu2, sigma2, eps=1e-6):
"""Numpy implementation of the Frechet Distance.
Taken from https://github.com/bioinf-jku/TTUR
The Frechet distance between two multivariate Gaussians X_1 ~ N(mu_1, C_1)
and X_2 ~ N(mu_2, C_2) is
d^2 = ||mu_1 - mu_2||^2 + Tr(C_1 + C_2 - 2*sqrt(C_1*C_2)).
Stable version by Dougal J. Sutherland.
Params:
-- mu1 : Numpy array containing the activations of a layer of the
inception net (like returned by the function 'get_predictions')
for generated samples.
-- mu2 : The sample mean over activations, precalculated on an
representive data set.
-- sigma1: The covariance matrix over activations for generated samples.
-- sigma2: The covariance matrix over activations, precalculated on an
representive data set.
Returns:
-- : The Frechet Distance.
"""
mu1, sigma1, mu2, sigma2 = mu1.detach().cpu().numpy(), sigma1.detach().cpu().numpy(), mu2.detach().cpu().numpy(), sigma2.detach().cpu().numpy()
mu1 = np.atleast_1d(mu1)
mu2 = np.atleast_1d(mu2)
sigma1 = np.atleast_2d(sigma1)
sigma2 = np.atleast_2d(sigma2)
assert mu1.shape == mu2.shape, \
'Training and test mean vectors have different lengths'
assert sigma1.shape == sigma2.shape, \
'Training and test covariances have different dimensions'
diff = mu1 - mu2
# Product might be almost singular
covmean, _ = linalg.sqrtm(sigma1.dot(sigma2), disp=False)
if not np.isfinite(covmean).all():
msg = ('fid calculation produces singular product; '
'adding %s to diagonal of cov estimates') % eps
print(msg)
offset = np.eye(sigma1.shape[0]) * eps
covmean = linalg.sqrtm((sigma1 + offset).dot(sigma2 + offset))
# Numerical error might give slight imaginary component
if np.iscomplexobj(covmean):
#print('wat')
if not np.allclose(np.diagonal(covmean).imag, 0, atol=1e-3):
m = np.max(np.abs(covmean.imag))
#print('Imaginary component {}'.format(m))
covmean = covmean.real
tr_covmean = np.trace(covmean)
out = diff.dot(diff) + np.trace(sigma1) + np.trace(sigma2) - 2 * tr_covmean
return out
mu和sigma,首先转换为numpy格式:

特征均值之间的差值:

sigma1和sigma2之间相乘求平方根。

求covmean的迹:

最后带入整个公式:

最后的输出值写入到log里面。