基于Python手写数字的识别【100010965】

基于Python手写数字的识别

一、总体方案

1.1 题目分析

使用 Python 实现对手写数字的识别工作，通过使用 windows 上的画图软件绘制一个大小是 28x28 像素的数字图像，图像的背景色是黑色，数字的颜色是白色，将该绘制的图像作为输入，经过训练好的模型识别所画的数字。

1.2 总体方案设计

手写数字的识别可以分成两大板块：一、手写数字模型的训练；二、手写数字的识别。其中最为关键的环节是手写数字模型的训练。下图为程序设计的总体流程。

本次选取使用的模型是多元线性回归模型。手写数字有 10 中，分别是 0~9，所以可以将该问题视为一个多分类问题。

二、算法基本原理

一个问题含有多个变量因素是，我们把包括两个或两个以上自变量的回归称为多元线性回归。多元线性回归的基本原理和基本计算过程与一元线性回归相同，不同的地方在于进行计算的变量个数是非常多的。由于在进行手写数字识别时，存在着 10 种数字，所以在进行标记训练数据集的标签时，通过热编码的方式来进行标签标记。下图展示了热编码的效果。

多元线性回归使用的是如下的公式进行计算的；

但是经过计算后 y 的值将会不在 0~1 内，而同时我们在进行标签标记时使用的是热编码，所以进行线性运算后需要将计算的结果转换到 0~1 之间，所以通过如下的公式：

该公式被称为 sigmoid 函数，其曲线当 y 的值越大时，y1 的结果越接近 1，当 y 的值越小时，y1 的结果越接近 0。下图为其函数曲线图。

利用上述的原理，进行一次训练，之后不断的进行运行，但是训练到何种程度算是结束训练呢，这就需要使用最小均方误差函数，使预测值与真实值之间的误差达到最小。下面的公式为最小均方误差函数表达式：

在进行迭代运算时，使用梯度下降的方法不断的对线性回归公式中的自变量参数 m1…mn 和 b 进行迭代更新，使最小均方误差函数达到最小。梯度计算时可以将最小均方误差进行求导，从而得到当前关于 m1…mn 和 b 的变化率，利用此变化率，来不断的更新当前的 m1…mn 和 b。如果我们将迭代的过程中最小均方误差的变化曲线如下图所示，图像红点所对应的地方的 m1…mn 和 b 值即为我们期望的。

所以根据以上的原理，进行训练的具体流程如下图所示：

得到训练后的权重后，在进行预测时通过使用公式

来计算该带预测的手写数字是 0~9 中的那个概率大，从而概率最大的就是预测的值。

三、系统实现

3.1 手写数字训练代码

import numpy as np


feature = np.loadtxt("train_image.csv", delimiter=",", max_rows=6000) / 255
          featureMatrix = np.append(feature, np.ones(shape=(len(feature), 1)), axis=1)

                          weightm = np.ones(shape=(feature.shape[1], 10))
                                    weightb = np.ones(shape=(1, 10))
                                            weight = np.r_[weightm, weightb]
                                                    learningrate = 0.0001

                                                            label = np.loadtxt("train_label_hotencoding.csv", delimiter=",", max_rows=6000)


                                                                    def grandientDecent():
                                                                        predict2sigmod = 1/ (1 + np.exp(-np.dot(featureMatrix, weight)))
                                                                                temp_slop = np.dot(featureMatrix.T, predict2sigmod - label)
                                                                                        return temp_slop


                                                                                                def train():
                                                                                                global weight
                                                                                                for i in range(1, 50000):
                                                                                                    slopmb = grandientDecent()
                                                                                                            weight -= slopmb * learningrate
                                                                                                                    return weight


                                                                                                                    if __name__ == '__main__':
                                                                                                                            myweight = train()
                                                                                                                                        np.savetxt("myweight1.csv",myweight,  fmt="%f", delimiter=",")

当把训练程序运行完成后会得到线性回归的权重值，并将数据保存到 myweight1.csv 文件中去。在训练程序中 train_image.csv 是训练集数据，train_label_hotencoding.csv 是对应与训练数据集的标签。

3.2 预测程序

import numpy as np
from PIL import Image

image = Image.open("D:/8.bmp")
        t = np.array(image) / 255



            testfeature = t.reshape(1,784)


                          np.set_printoptions(threshold=np.inf, suppress=True)


                          myweight = np.loadtxt("myweight1.csv", delimiter=",")

                                     testfeatureMatrix = np.append(testfeature, np.ones(shape=(len(testfeature), 1)), axis=1)
                                             mypredict = np.dot(testfeatureMatrix, myweight)
                                                     expmpre = np.exp(mypredict)
                                                             expsum = np.sum(expmpre, axis=1)

                                                                     for i in range(len(testfeature)):
                                                                             expmpre[i, :] = expmpre[i, :] / expsum[i]
                                                                                     pre = np.argmax(expmpre[i, :])
                                                                                             print(pre)

                                                                                             print("-" * 20)

程序首先是对我们手写的数字进行处理，将其转换成与训练集相同格式的数据，之后是加载线性回归的权重模型 myweight1.csv

四、程序效果

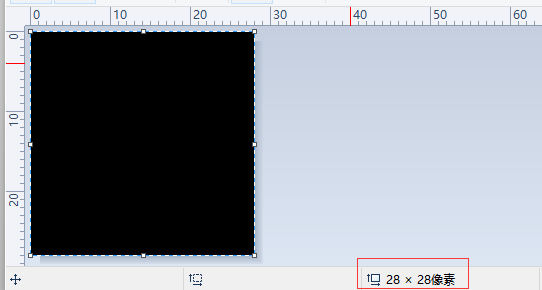
画图软件画图界面里的要求如下图：必须是黑色的底白色的字，并且保存的图片的大小是 28x28 的，这样就与训练的数据集向吻合。

手写数字后识别界面：

其识别效果如下图：

但是在进行测试的时候仍然会存在着一定的问题，经过查询相关的资料发现是由于进行训练时出现了过拟合现象，所以仍需继续学习。

♻️ 资源

大小： 265KB
➡️ 资源下载：https://download.csdn.net/download/s1t16/87490655
注：如当前文章或代码侵犯了您的权益，请私信作者删除！