《剑指offer》（3）排序算法篇

class Solution:

    def duplicate(self , numbers: List[int]) -> int:

        if len(numbers) <= 1:

            return -1

        import collections

        num_dict = collections.Counter(numbers)

        res = [key for (key,value) in num_dict.items() if value > 1]

        return res[0]

class Solution:

    def sort(self,num): #快排

        if len(num) <= 1:

            return num

        import random

        pivot = random.choice(num)

        left = self.sort([i for i in num if i < pivot])

        right = self.sort([i for i in num if i > pivot])

        same = [i for i in num if i == pivot]

        return left+same+right

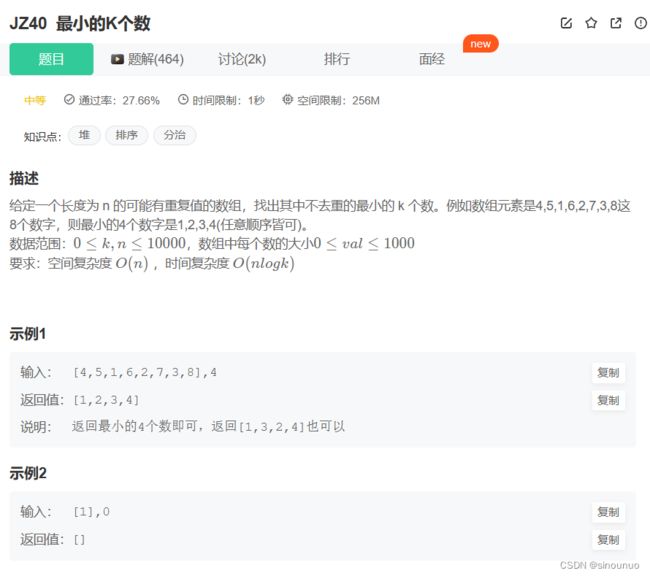
    def GetLeastNumbers_Solution(self , input: List[int], k: int) -> List[int]:

        if k > len(input) or k == 0: #对数据进行错误判断

            return []

        res = self.sort(input)

        return res[:k]

 #插入排序

class Solution:

    def __init__(self) -> None:

        self.res = []

    def Insert(self, num): #插入排序

        if len(self.res) == 0:

            self.res.append(num)

        else:

            i = 0

            while i < len(self.res):

                if num <= self.res[i]:

                    break

                i += 1

            self.res.insert(i,num)

    def GetMedian(self):

        n = len(self.res)

        if n % 2 == 0:

            return (self.res[n//2]+self.res[n//2-1])/2.0

        else:

            return self.res[n//2]

class Solution:

    def merge(self,num): #使用类似于快排的方式

        if len(num) <= 1:

            return 0

        bigger = []  #比基准大的数字

        smaller = [] #比基准小的数字

        prev = num[0] #选取第一个数作为基准

        res = 0

        for i in num[1:]: #遍历剩下的数组

            if i > prev: #如果大于基准（不是逆序对）

                bigger.append(i) #放到bigger中

            else: #是逆序对

                smaller.append(i) #放到smaller中，此时对于small中的每一个数，逆序对都至少等于bigger中的个数（不考虑smaller内部情况）

                res += len(bigger) + 1 if num[i] < prev else len(bigger) #如果严格不等值，就得加上基准，否则不加

        return res+self.merge(bigger)+self.merge(smaller) #递归去查看bigger和smaller中的情况

    def InversePairs(self , nums: List[int]) -> int:

        return self.merge(nums)%1000000007