FcaNet: Frequency Channel Attention Networks

主要贡献在于把channel attention改为multi-spectral channel attention

Abstract

注意力机制，尤其是通道注意力，在计算机视觉领域取得了巨大的成功。许多研究集中于如何设计有效的通道注意力机制，而忽略了一个根本问题，即通道注意力机制使用标量来表示通道，这是由于大量信息丢失而带来的困难。在这项工作中，我们从不同的角度出发，利用频率分析将信道表示问题视为一个压缩过程。基于频率分析，我们从数学上证明了传统的全局平均池是频域特征分解的特例。通过证明，我们自然地在频域推广了信道注意力机制的压缩，并提出了多光谱信道注意力的方法，称为FcaNet。FcaNet简单但有效。我们可以在计算中更改几行代码，以便在现有的channel注意力方法中实现我们的方法。此外，与其他通道注意力方法相比，该方法在图像分类、目标检测和实例分割任务方面取得了最新的结果。在相同的参数数量和相同的计算成本下，我们的方法可以始终优于基线SENet。

预备知识

GAP

全局平均池化是在论文Network in Network中提出的

如果要预测K个类别，在卷积特征抽取部分的最后一层卷积层，就会生成K个特征图，
然后通过全局平均池化就可以得到 K个1×1的特征图，将这些1×1的特征图输入到softmax layer之后，每一个输出结果代表着这K个类别的概率（或置信度 confidence），起到取代全连接层的效果。

优点：

• 和全连接层相比，使用全局平均池化技术，对于建立特征图和类别之间的关系，是一种更朴素的卷积结构选择。
• 全局平均池化层不需要参数，避免在该层产生过拟合。
• 全局平均池化对空间信息进行求和，对输入的空间变化的鲁棒性更强。

DTC（离散余弦变换）

DCT，即离散余弦变换，常用图像压缩算法，步骤如下：

• 首先将图像分割成8x8或16x16的小块；
• DCT变换，对每个小块进行DCT变换；
• 舍弃高频系数（AC系数），保留低频信息（DC系数）。高频系数一般保存的是图像的边界、纹理信息，低频信息主要是保存的图像中平坦区域信息。
  图像的低频和高频，高频区域指的是空域图像中突变程度大的区域（比如目标边界区域），通常的纹理丰富区域。

二维DCT变换就是将二维图像从空间域转换到频率域。形象的说，就是计算出图像由哪些二维余弦波构成，其主要用于数据或图像的压缩，能够将空间域的信号转换到频域上，具有良好的去相关性的性能。二维的DTC​​公式如下：
$${\mathrm{f}}_{\mathrm{h},\mathrm{w}}^{2\mathrm{d}}=\sum _{\mathrm{i}=0}^{\mathrm{H}-1}\sum _{\mathrm{j}=0}^{\mathrm{W}-1}{\mathrm{x}}_{\mathrm{i},\mathrm{j}}^{2\mathrm{d}}\cos \left(\frac{\pi \mathrm{h}}{\mathrm{H}}\left(\mathrm{i}+\frac{1}{2}\right)\right)\cos \left(\frac{\pi \mathrm{h}}{\mathrm{W}}\left(\mathrm{j}+\frac{1}{2}\right)\right)$$
二维的逆DTC公式如下:
$${\mathrm{x}}_{\mathrm{h},\mathrm{w}}^{2\mathrm{d}}=\sum _{\mathrm{h}=0}^{\mathrm{H}-1}\sum _{\mathrm{w}=0}^{\mathrm{W}-1}{\mathrm{f}}_{\mathrm{i},\mathrm{j}}^{2\mathrm{d}}\cos \left(\frac{\pi \mathrm{h}}{\mathrm{H}}\left(\mathrm{i}+\frac{1}{2}\right)\right)\cos \left(\frac{\pi \mathrm{h}}{\mathrm{W}}\left(\mathrm{j}+\frac{1}{2}\right)\right)$$
我们称二者的共有项为基函数:
$${\mathrm{B}}_{\mathrm{h},\mathrm{w}}^{\mathrm{i},\mathrm{j}}=\cos \left(\frac{\pi \mathrm{h}}{\mathrm{H}}\left(\mathrm{i}+\frac{1}{2}\right)\right)\cos \left(\frac{\pi \mathrm{h}}{\mathrm{W}}\left(\mathrm{j}+\frac{1}{2}\right)\right)$$ 当h=0、w=0时，就等价于GAP

本文method

传统的通道注意方法致力于构建各种通道重要性权重函数，这种权重函数要求每个通道都有一个标量来进行计算，由于计算开销有限，简单有效的全局平均池化（GAP）成为了他们的不二之选。但是一个潜在的问题是GAP​是否能够捕获丰富的输入信息，也就是说，仅仅平均值是否足够表示通道注意力中的各个通道。

GAP的不足与分析：
1）不同的通道可能拥有相同的平均值，而其代表的语义信息是不相同的；
2）从频率分析的角度，可以证明GAP等价于DCT​​的最低频率，仅仅使用GAP相当于丢弃了其他许多包含着通道特征的信息；
3）CBAM还表示，仅使用GAP是不够的，因此额外引入了GMP​。​

Revisiting DCT and Channel Attention

Channel Attention

通道注意力机制在 CNN 中广泛应用。它使用一个可学习的网络对各个通道的重要度加权，生成更有意义的输出。假设 $X\in {\mathbb{R}}^{C\times H\times W}$是图像特征张量， C是通道数， H,W分别是特征图的高度和宽度。然后该注意力机制可以写成：$$att=sigmoid(fc(compress(X))),\text{\hspace{1em}(4)}$$其中 $att\in {\mathbb{R}}^C$ 是注意力向量，sigmoid是Sigmoid函数， $fc$表示全连接层或一维卷积的映射函数， compress表示一个通道压缩方法，例如，全局平均池化。得到所有 C个通道的注意力向量后，输入 X 的每个通道都用下面对应的注意力值来缩放：$${\tilde{X}}_{:,:,i,:}=at{t}_i{X}_{:,:,i,:}s.t.i\in \{0,1,...,C-1\},\text{\hspace{1em}(5)}$$ $\tilde{X}$是注意力机制的输出， $at{t}_i$ 是注意力向量中第 i 个元素，$X_{:,i,:,:}$ 是输入的第个通道。

有了通道注意力和DCT的定义，我们可以总结出2个关键特性：
a) 在通道注意力之前，现有方法使用 GAP 来做预处理。
b) DCT 可以看作为一个输入加权的和，用了等式3和等式4中的余弦部分作为权重。

GAP 是均值操作，算力消耗有限，是最简单的输入频谱了。但在通道注意力机制中仅使用 GAP 信息是不足够的。受这些特点启发，作者就提出了多频谱通道注意力方法。

Multi-Spectral Channel Attention

出于简洁性，作者使用 B 来表示2D DCT的基函数：$$B_{i,j}^{h,w}=cos(\frac{\pi h}{H}(i+\frac{1}{2}))cos(\frac{\pi w}{W}(j+\frac{1}{2}))$$
那么 2D DCT 就可以写成：
$$\begin{array}{l}{x}_{i,j}^{2d}={\sum }_{h=0}^{H-1}{\sum }_{w=0}^{W-1}{f}_{h,w}^{2d}\cos \left(\frac{\pi h}{H}\left(i+\frac{1}{2}\right)\right)\cos \left(\frac{\pi w}{W}\left(j+\frac{1}{2}\right)\right)\\ \stackrel{\text{ Eq. }7}{=}{f}_{0,0}^{2d}{B}_{0,0}^{i,j}+f_{0,1}^{2d}{B}_{0,1}^{i,j}+\cdots +f_{H-1,W-1}^{2d}{B}_{H-1,W-1}^{i,j}\\ \stackrel{\text{ Eq. }6}{=}\mathrm{gap}\left(x^{2d}\right)HW{B}_{0,0}^{i,j}+f_{0,1}^{2d}{B}_{0,1}^{i,j}+\cdots +f_{H-1,W-1}^{2d}{B}_{H-1,W-1}^{i,j}\\ \text{ s.t. }i\in \{0,1,\cdots ,H-1\},j\in \{0,1,\cdots ,W-1\}\text{. }\end{array}$$很明显，一个图像或特征可以用不同频率组成的组合表示。

通道注意力只是基于 GAP 的结果。但是从等式8中，我们可以看到输入 X的信息并不只是由 GAP 构成的：$$X=\underset{\text{utilized }}{gap(X)HW{B}_{0,0}^{i,j}}+\underset{\text{discarded }}{f_{0,1}^{2d}{B}_{0,1}^{i,j}+\cdots +f_{H-1,W-1}^{2d}{B}_{H-1,W-1}^{i,j}}.$$这样在通道注意力机制中，只用到了一小部分的信息。在现有的通道注意力方法中都没有包含其它频率组成和信息。

Multi-Spectral Channel Attention Module

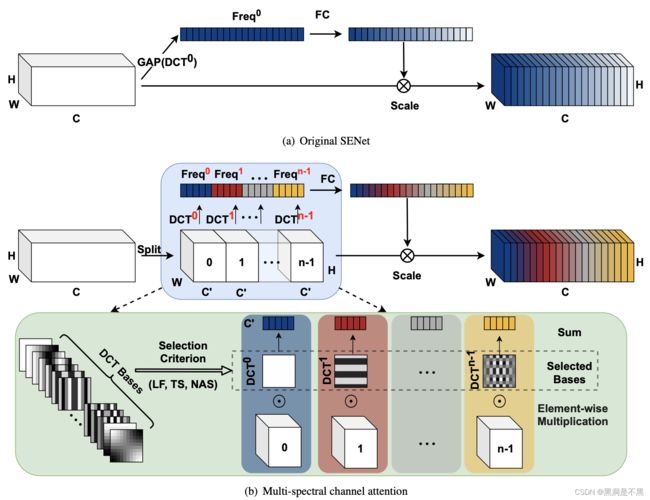
基于定理1的分析，作者发现现有的通道注意力方法所使用的信息都是不充分的，通道注意力的 GAP 方法只是 2D DCT 的一个特例。那么，我们就可以引入2D DCT更多的频率组成，引入更多的信息来解决信息不充分的问题。

为了引入更多的信息，作者提出使用2D DCT的多个频率组成，包括最低的频率组成，即 GAP。

首先沿着通道维度，输入 X被分为多个部分。用$[X_0,X_1,...,X_{n-1}]$表示这些部分，其中 $X^i\in {\mathbb{R}}^{C^{\prime }\times H\times W},i\in \{0,1,...,n-1\},C^{\prime }=\frac{C}{n}$，其中 C 可以被 n 整除。对于每个部分，都会赋予一个对应的2D DCT频率组成，2D DCT结果可以作为通道注意力预处理的结果。这样，我们有：

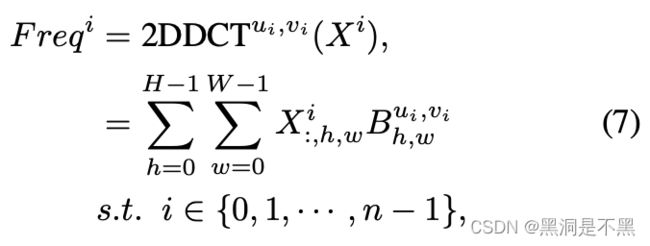
其中[u,v]是频率组成的2D索引，对应着 $X^i$ ， $Fre{q}^i\in {\mathbb{R}}^{C^{\prime }}$是预处理之后的 C’ 维向量。通过 concat 操作可以获取整个预处理向量：
$$\begin{gathered} Freq \\ =compress(X) \\ =cat([Fre{q}^0,...,Fre{q}^{n-1}])\text{\hspace{1em}(8)} \end{gathered}$$
$Fre{q}^i\in {\mathbb{R}}^C$是多频谱向量。整个多频谱通道注意力框架可以写为：$$ms\_attn=sigmoid(Fc(Freq))\text{\hspace{1em}(9)}$$

Criteria for Choosing Frequency Component

如何为每个部分$X_i$ 选择频率分量索引$[u_i,v_i]$存在一个重要问题。为了充分满足多频谱信道的关注，我们提出了三种标准，即FcaNet-LF（低频）、FcaNet-TS（两步选择）和FcaNet-NAS（神经架构搜索）。

FcaNet-LF
FcaNet-LF指具有低频成分的FcaNet。众所周知，许多压缩方法使用DCT的低频信息来压缩信息。此外，一些方法[21，41]表明，神经网络更喜欢低频信息。这样，选择频率分量的第一个标准就是只选择低频分量。
FcaNet-TS
FcaNet-TS表示FcaNet在两步选择方案中选择组件。其主要思想是首先确定每个频率分量的重要性，然后研究使用不同数量频率分量的影响。也就是说，我们单独评估频道注意力中每个频率分量的结果。最后，我们根据评估结果选择了Top-k最高性能的频率组件。
FcaNet-NAS
FcaNet-NAS指具有搜索组件的FcaNet。对于这个标准，我们使用神经结构搜索来搜索信道的最佳频率分量。对于每个部分$X_i$，一组连续变量$\alpha =\{{\alpha }^{(u,v)}\}$作为符号用于搜索组件。该部分的频率分量可写成：