已知中心点、长宽和旋转角度,求矩形的四个顶点坐标(Python)
已知中心点、长宽和旋转角度,求矩形的四个顶点坐标
- 理论基础
-
- 情况一: θ ∈ [ 0 , π / 2 ] \theta \in [0, \pi/2] θ∈[0,π/2]
- 情况二: θ ∈ [ π / 2 , π ] \theta \in [ \pi/2,\pi] θ∈[π/2,π]
- python代码实现
理论基础
本次实现有几个前提:
- 已知的信息如下形式:[x_center, y_center, w, h, angle],其中默认 w w w是矩形最长的边,即 w > h w > h w>h。
- 已知的旋转角度 θ \theta θ是矩形的最长边 w w w相对于 x x x坐标轴的旋转角度
- 旋转角度 θ \theta θ的旋转区间在 [ 0 , π ] [0, \pi] [0,π]
可以将情况分为两种,即 θ ∈ [ 0 , π / 2 ] \theta \in [0, \pi/2] θ∈[0,π/2]和 θ ∈ [ π / 2 , π ] \theta \in [\pi/2, \pi] θ∈[π/2,π]
情况一: θ ∈ [ 0 , π / 2 ] \theta \in [0, \pi/2] θ∈[0,π/2]
先看第一种情况 θ ∈ [ 0 , π / 2 ] \theta \in [0, \pi/2] θ∈[0,π/2]:
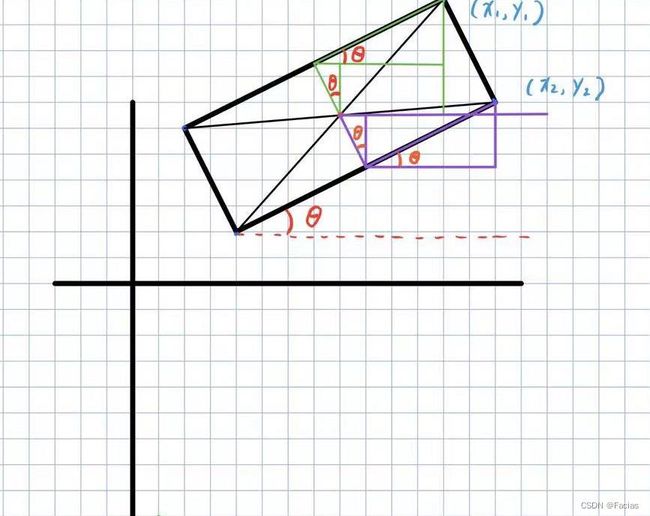
已知矩形的中心点 ( x , y ) (x, y) (x,y),旋转角度 θ \theta θ在图中用橙色标注。
先来求 ( x 1 , y 1 ) (x_1,y_1) (x1,y1),用到图中绿色的辅助线,用到的三角形都标注了角 θ \theta θ:
- x 1 = x + c o s θ ∗ w / 2 − s i n θ ∗ h / 2 x_1=x+cos\theta*w/2-sin\theta*h/2 x1=x+cosθ∗w/2−sinθ∗h/2
- y 1 = y + s i n θ ∗ w / 2 + c o s θ ∗ h / 2 y_1=y+sin\theta*w/2+cos\theta*h/2 y1=y+sinθ∗w/2+cosθ∗h/2
再来求 ( x 2 , y 2 ) (x_2,y_2) (x2,y2),用到图中紫色的辅助线:
- x 2 = x + c o s θ ∗ w / 2 + s i n θ ∗ h / 2 x_2=x+cos\theta*w/2+sin\theta*h/2 x2=x+cosθ∗w/2+sinθ∗h/2
- y 2 = y + s i n θ ∗ w / 2 − c o s θ ∗ h / 2 y_2=y+sin\theta*w/2-cos\theta*h/2 y2=y+sinθ∗w/2−cosθ∗h/2
接下来的 ( x 3 , y 3 ) (x_3,y_3) (x3,y3)和 ( x 4 , y 4 ) (x_4,y_4) (x4,y4)就是 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)和 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)关于 ( x , y ) (x, y) (x,y)的对称点,只需要将正项变为负项,负项变为正项即可:
- x 3 = x − c o s θ ∗ w / 2 + s i n θ ∗ h / 2 x_3=x-cos\theta*w/2+sin\theta*h/2 x3=x−cosθ∗w/2+sinθ∗h/2
- y 3 = y − s i n θ ∗ w / 2 − c o s θ ∗ h / 2 y_3=y-sin\theta*w/2-cos\theta*h/2 y3=y−sinθ∗w/2−cosθ∗h/2
- x 4 = x − c o s θ ∗ w / 2 − s i n θ ∗ h / 2 x_4=x-cos\theta*w/2-sin\theta*h/2 x4=x−cosθ∗w/2−sinθ∗h/2
- y 4 = y − s i n θ ∗ w / 2 + c o s θ ∗ h / 2 y_4=y-sin\theta*w/2+cos\theta*h/2 y4=y−sinθ∗w/2+cosθ∗h/2
情况二: θ ∈ [ π / 2 , π ] \theta \in [ \pi/2,\pi] θ∈[π/2,π]
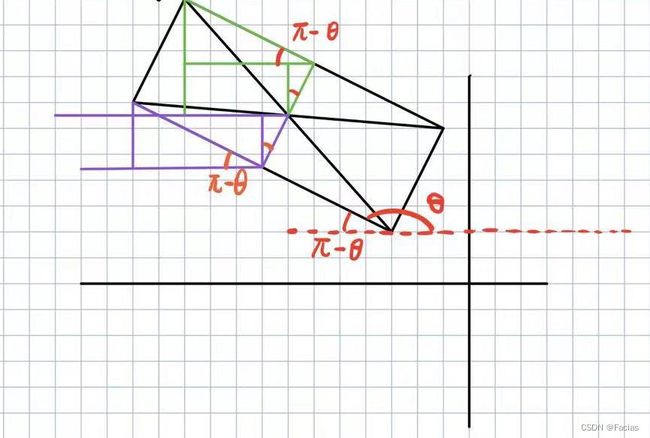
同理,此时旋转角度 θ \theta θ大于 π / 2 \pi/2 π/2,所以用到的辅助三角形的角度标注为 π − θ \pi -\theta π−θ。
先来求 ( x 1 , y 1 ) (x_1,y_1) (x1,y1),用到图中绿色的辅助线,用到的三角形都标注了角 π − θ \pi -\theta π−θ:
- x 1 = x − c o s ( π − θ ) ∗ w / 2 + s i n ( π − θ ) ∗ h / 2 = x + c o s θ ∗ w / 2 + s i n θ ∗ h / 2 x_1=x-cos(\pi-\theta)*w/2+sin(\pi-\theta)*h/2=x+cos\theta*w/2+sin\theta*h/2 x1=x−cos(π−θ)∗w/2+sin(π−θ)∗h/2=x+cosθ∗w/2+sinθ∗h/2
- y 1 = y − s i n ( π − θ ) ∗ w / 2 − c o s ( π − θ ) ∗ h / 2 = y − s i n θ ∗ w / 2 + c o s θ ∗ h / 2 y_1=y-sin(\pi-\theta)*w/2-cos(\pi-\theta)*h/2=y-sin\theta*w/2+cos\theta*h/2 y1=y−sin(π−θ)∗w/2−cos(π−θ)∗h/2=y−sinθ∗w/2+cosθ∗h/2
- x 2 = x − c o s ( π − θ ) ∗ w / 2 − s i n ( π − θ ) ∗ h / 2 = x + c o s θ ∗ w / 2 − s i n θ ∗ h / 2 x_2=x-cos(\pi-\theta)*w/2-sin(\pi-\theta)*h/2=x+cos\theta*w/2-sin\theta*h/2 x2=x−cos(π−θ)∗w/2−sin(π−θ)∗h/2=x+cosθ∗w/2−sinθ∗h/2
- y 2 = y + s i n ( π − θ ) ∗ w / 2 − c o s ( π − θ ) ∗ h / 2 = y + s i n θ ∗ w / 2 + c o s θ ∗ h / 2 y_2=y+sin(\pi-\theta)*w/2-cos(\pi-\theta)*h/2=y+sin\theta*w/2+cos\theta*h/2 y2=y+sin(π−θ)∗w/2−cos(π−θ)∗h/2=y+sinθ∗w/2+cosθ∗h/2
( x 3 , y 3 ) (x_3,y_3) (x3,y3)和 ( x 4 , y 4 ) (x_4,y_4) (x4,y4)就是 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)和 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)关于 ( x , y ) (x, y) (x,y)的对称点。
可以看到两种情况下,得到的四个点的值是一样的,比如情况一里 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)和情况二里 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)一样,所以在代码实现里可以不分情况讨论,不影响最终结果。
python代码实现
def get_corners(box): #这里本人项目yaw [-pi/4, 3*pi/4),需要映射到[0, pi)
box = box.detach().cpu().numpy()
x = box[0]
y = box[1]
w = box[2]
l = box[3]
yaw = box[4]
if yaw <0: #用来映射
yaw = yaw + np.pi
bev_corners = np.zeros((4, 2), dtype=np.float32)
cos_yaw = np.cos(yaw)
sin_yaw = np.sin(yaw)
bev_corners[0, 0] = (w / 2) * cos_yaw - (l / 2) * sin_yaw +x
bev_corners[0, 1] = (w / 2)* sin_yaw + (l / 2) * cos_yaw +y
bev_corners[1, 0] = (l / 2) * sin_yaw + (w / 2) * cos_yaw +x
bev_corners[1, 1] = (w / 2)* sin_yaw - (l / 2) * cos_yaw +y
bev_corners[2, 0] = (-w / 2) * cos_yaw - (-l / 2) * sin_yaw +x
bev_corners[2, 1] = (-w / 2)* sin_yaw + (-l / 2) * cos_yaw +y
bev_corners[3, 0] = (-l / 2) * sin_yaw + (-w / 2) * cos_yaw +x
bev_corners[3, 1] = (-w / 2)* sin_yaw - (-l / 2) * cos_yaw +y
return bev_corners