算法通关村—轻松搞定二叉树里面的双指针
1. 相同的树
相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
输入:p = [1,2,3], q = [1,2,3]
输出:true
1.1 深度优先
需要判断两个二叉树是不是空的,然后再判断是否有一个是空的,接下来使用递归左子树和右子树的比较。
public boolean isSameTree(TreeNode p, TreeNode q) {
// 两者都为空
if(p == null && q==null) return true;
// 两者有一个为空
if(p==null || q == null) return false;
if(p.val!=q.val){
return false;
}
// 递归
return isSameTree(p.left,q.left) && isSameTree(p.right,q.right);
}
这里面需要注意的是&&放在||的前面,一开始没注意,出错了才发现逻辑不对。
1.2 广度优先
借助队列来存储二叉树元素,然后比较两个节点的值是否相等,不等就直接退出,相等就继续往左子树右子树遍历。
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p==null && q == null) return true;
if(p == null || q==null) return false;
Queue<TreeNode> queue1 = new LinkedList<TreeNode>();
Queue<TreeNode> queue2 = new LinkedList<TreeNode>();
queue1.offer(p);
queue2.offer(q);
while(!queue1.isEmpty() && !queue2.isEmpty()){
TreeNode node1=queue1.remove();
TreeNode node2 = queue2.remove();
if(node1.val!=node2.val){
return false;
}
TreeNode left1 = node1.left,right1=node1.right;
TreeNode left2 = node2.left,right2=node2.right;
// 使用异或来判断是否有子节点
if(left1==null ^ left2==null) return false;
if(right1==null ^ right2==null) return false;
if(left1!=null) queue1.offer(left1);
if(right1!=null) queue1.offer(right1);
if(left2!=null) queue2.offer(left2);
if(right2!=null) queue2.offer(right2);
}
return queue1.isEmpty() && queue2.isEmpty();
}
虽然这个里面有很多的if语句判断,但是理解起来还是不难。
2. 对称二叉树
对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
2.1 递归
主要思路就是将子树的左子树和右子树是进行比较。将一个二叉树从根节点拆分成了两个二叉树,和第一道题目类似,由于对称的特性,需要将第一个子树的左节点和第二个子树的右节点进行比较,使用递归标识还是简单的。
public boolean isSymmetric(TreeNode root) {
if(root == null ) return true;
return check(root.left,root.right);
}
public boolean check(TreeNode p,TreeNode q){
if(p == null && q==null) return true;
if(p==null || q ==null) return false;
return p.val == q.val && check(p.left,q.right) && check(p.right,q.left);
}
2.2 迭代
也是分成两个二叉树,但是这次使用队列只需要使用一个就行,按照队列出来的先后顺序就能直到是左子树还是右子树。
public boolean isSymmetric(TreeNode root) {
if(root == null || (root.left==null && root.right==null)) return true;
Queue<TreeNode> queue = new LinkedList<>();
queue.add(root.left);
queue.add(root.right);
while(!queue.isEmpty()){
TreeNode left = queue.remove();
TreeNode right = queue.remove();
if(left == null && right == null) continue;
if(left==null || right==null) return false;
if(left.val!=right.val) return false;
// 左孩子的左节点和右孩子的右节点比较
queue.add(left.left);
queue.add(right.right);
// 左节点的右孩子和右节点的左孩子放入队列
queue.add(left.right);
queue.add(right.left);
}
return true;
}
3. 合并二叉树
合并二叉树
给你两棵二叉树: root1 和 root2 。
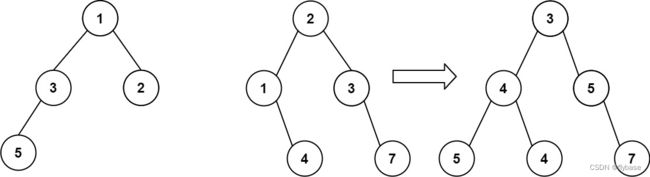
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
3.1 递归/ 深度优先
一开始真没想到怎么做,主要思路是创建一个新的二叉树,然后让相应的子树相加递归,就是新的二叉树的子树,然后返回就可以。
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if(root1==null) return root2;
if(root2==null) return root1;
// 先记录下当前两个节点的之和
TreeNode merged = new TreeNode(root1.val+root2.val);
// 新子树的左节点通过递归获取
merged.left=mergeTrees(root1.left,root2.left);
merged.right=mergeTrees(root1.right,root2.right);
return merged;
}
3.2 迭代/ 广度
依然是造树,但是需要使用三个队列来存储对应树的节点,然后分别相加两个数的左子树的值和右子树的值,新的二叉树的左右子树就出来了。
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if(root1 == null) return root2;
if(root2 == null) return root1;
TreeNode merged = new TreeNode(root1.val+root2.val);
// 存储新二叉树
Queue<TreeNode> queue = new LinkedList<>();
// 存储root1
Queue<TreeNode> queue1 = new LinkedList<>();
// 存储root2
Queue<TreeNode> queue2 = new LinkedList<>();
queue.offer(merged);
queue1.offer(root1);
queue2.offer(root2);
while(!queue.isEmpty() && !queue1.isEmpty() && !queue2.isEmpty()){
TreeNode node = queue.remove();
TreeNode node1 = queue1.remove();
TreeNode node2 = queue2.remove();
TreeNode left1 = node1.left,right1=node1.right;
TreeNode left2 = node2.left,right2=node2.right;
// 左节点合并
if(left1!= null || left2!=null){
if(left1!=null && left2!=null){
TreeNode left = new TreeNode(left1.val+left2.val);
node.left = left;
queue.offer(left);
queue1.offer(left1);
queue2.offer(left2);
}else if(left1!=null){
node.left = left1;
}else{
node.left = left2;
}
}
// 右节点合并
if(right1!=null || right2!=null){
if(right1!=null && right2!=null){
TreeNode right = new TreeNode(right1.val+right2.val);
node.right = right;
queue.offer(right);
queue1.offer(right1);
queue2.offer(right2);
}else if(right1!=null){
node.right = right1;
}else{
node.right = right2;
}
}
}
return merged;
}
缺点:使用了三个队列来分别存储三个二叉树的值,很浪费空间,代码也是比较多的。
时间复杂度:O(min(m,n))其中m,n代表两个二叉树的节点个数
空间复杂度:O(min(m,n))取决于队列里面的元素个数。
总结
上面几个方法都是使用递归,也就是深度遍历,代码量少,而且清晰易懂,而迭代,广度遍历使用的代码量比较多,而且每次都需要使用相应的队列来存储元素。