【C语言】全排列算法（回溯+递归）——找出找出走通五个地方最短路径
目录
一、预览
1. 测试文件（test.c）
2. 函数的声明（game.h）
3. 函数的实现（game.c）
二、重点突破
1. 打印菜单 && 生成不重复的五个城市坐标
2. 记录两两城市的距离
※ 3. 全排列算法
方法一（回溯）
方法二（简单递归）
4. 计算比较 && 打印最短路径
summery
“
这个小案例的重难点就是用递归列出全排列，还有一个注意的事项就是防止生成的随机坐标不能重复
”
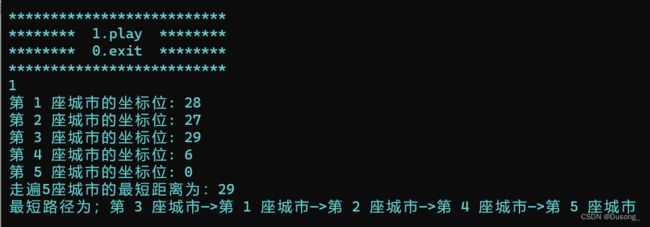
一、预览
还是老样子，先上代码⬇️
1. 测试文件（test.c）
#include"game.h"
void menu()
{
printf("**************************\n");
printf("******** 1.play ********\n");
printf("******** 0.exit ********\n");
printf("**************************\n");
}
void game()
{
int city[5] = { 0 }; //数组五个元素代表五个城市
int citys[5][5] = { 0 }; //存放两两城市的距离
Initcity(city); //生成随机坐标，放在city数组中
dest_city(city,citys); //计算两两城市的距离
MIN_dest(citys); //找出最短路径并打印
}
void test()
{
srand((unsigned int)time(NULL)); //生成随机数
int input = 0;
do
{
menu();
scanf("%d", &input);
switch (input)
{
case 1:
game();
break;
case 0:
printf("退出游戏\n");
break;
default:
printf("输入错误，请重新输入\n");
break;
}
} while (input);
}
int main()
{
system("color 0B"); //设置颜色（可略）
test();
return 0;
}2. 函数的声明（game.h）
#pragma once
#include
#include
#include
#include
void Initcity(int *city);
void dest_city(int* city, int citys[5][5]);
void MIN_dest(int citys[5][5]); 3. 函数的实现（game.c）
#include"game.h"
void Initcity(int *city) //生成随机坐标，放入city数组中
{
for (int i = 0; i < 5; i++)
{
int jud = 0;
do //防止坐标重复
{
jud = 0;
int tmp = rand() % 30;
city[i] = tmp;
for (int j = 0; j < i; j++)
{
if (city[i] == city[j])
jud = 1; //发现有重复坐标，将jud = 1，循环，再次生成随即坐标
}
} while (jud);
printf("第 %d 座城市的坐标位: %d\n", i+1, city[i]);
}
}
//将两两城市的距离（坐标差值的绝对值）放入二维数组中
void dest_city(int* city, int citys[5][5])
{
for (int i = 0; i < 5; i++)
{
for (int j = 0; j < 5; j++)
{
int tmp = (city[i] - city[j]);
tmp = tmp > 0 ? tmp : (-tmp);
citys[i][j] = tmp;
}
}
}
//m,n——数组长度， min——最短距离， dest——临时存放城市的排列， tmp——方法一所用， min_path——存放最短路径， citys[5][5]——用来计算路程总和
void Full_arrangement(int m, int n, int* min, int* dest, int* tmp,int* min_path,int citys[5][5])
{
if (m == n)
{
int sum = 0;
for (int i = 0; i < 4; i++)
{
sum += citys[dest[i]][dest[i + 1]];
}
if (sum < *min)
{
*min = sum; //这里需要用指针，不然改变的是形参
for (int j = 0; j < 5; j++)
{
min_path[j] = dest[j]; //将最短路径保存下来
}
}
}
else
{
//方法一
for (int i = 0; i < n; i++)
{
if (tmp[i] == 0)
{
tmp[i] = 1;
dest[m] = i ;
Full_arrangement(m + 1, n,min, dest, tmp,min_path,citys);
tmp[i] = 0;
}
}
/*
//方法二(该方法需要将dest数组初始化为{0，1，2，3，4})
for (i = m; i < n; i++)
{
Swap(&dest[m],&dest[i]);
Full_arrangement(m + 1, n,min, dest,min_path,citys);
Swap(&dest[m],&dest[i]);
}
*/
}
}
void Printmin_path(int min,int* min_path) //打印最短路径及最短距离
{
printf("走遍5座城市的最短距离为：%d\n", min);
printf("最短路径为；");
for (int i = 0; i < 5; i++)
{
if (i == 4)
printf("第 %d 座城市\n", min_path[i] + 1);
else
printf("第 %d 座城市—>", min_path[i] + 1);
}
printf("\n");
}
void MIN_dest(int citys[5][5])
{
int dest[5];
int tmp[5]; //法一所用
int min = 500;
int min_path[5];
//数组初始化为0
memset(dest, 0, sizeof(dest));
memset(tmp, 0, sizeof(tmp));
memset(min_path, 0, sizeof(min_path));
Full_arrangement(0, 5,&min, dest, tmp,min_path,citys);
Printmin_path(min,min_path);
}
二、重点突破
1. 打印菜单 && 生成不重复的五个城市坐标
① 首先打印菜单，定义变量input，输入1表示进入游戏，输入0表示退出，输入其他则重新输入
② 用do-while循环，第一次不用判断直接进入循环，再用switch分支语句，根据input的值判断是开始游戏还是跳出循环，结束游戏
③ 用rand函数生成随机数
https://blog.csdn.net/Dusong_/article/details/127577970?spm=1001.2014.3001.5501
这里需要注意的是：两两城市的坐标肯定是不一样的，所以生成的随机数是不能一样的
解决方法： 每生成一个随机数，就需要对将其与之前存放在数组中的所有数比较一次，若有相等的数，则重新生成本次随机数，则生成五个不一样的随机数，需要比较1+2+3+4 = 10次；
我们用for循环中再套一层for循环就能实现了⬆️
详细代码请看上述函数： test() Initcity(int *city);
2. 记录两两城市的距离
① 二维数组citys[5][5]行列下标均为0-4，可以将两两城市的距离存放在以这两座城市分别为行列下标的二维数组中
详细代码请看上述函数： void dest_city(int* city, int citys[5][5])
※ 3. 全排列算法
我们全排列的算法抽出来单独解析：接下来用简单的三个数（1，2，3）的全排列为例子，画图解析下列两种方法⬇️
方法一（回溯）
回溯法较为抽象，大家可以选择性跳过，转到较为简单的方法二中⬇️
回溯算法其实我也不是很了解，通过这次练习之后此开始重视这个算法，所以本篇文章就不详细讲解了，之后我学习透彻之后会立即写博客分享
（回溯算法的博客我已经发出来啦，感兴趣的朋友可以点击链接去看看）【算法】当你站在流水线上解决《回溯》——全排列Ⅱ、组合总和Ⅱ、解数独_Dusong_的博客-CSDN博客
这里我将自己的递归的部分图解分享给大家，希望对大家有所帮助
void Full_arrangement(m + 1, n,min, dest, tmp,min_path,citys)
{
int i;
if (m == n)
{
for (i = 0; i < n - 1; i++)
printf("%d ", dest[i]);
printf("%d\n", dest[i]);
}
else
{
/*
int tmp[5];
memset(tmp, 0, sizeof(tmp));
*/
for (int i = 0; i < n; i++)
{
if (tmp[i] == 0)
{
tmp[i] = 1;
dest[m] = i ;
Full_arrangement(m + 1, n,min, dest, tmp,min_path,citys);
tmp[i] = 0;
}
}
}
}方法二（简单递归）
思路分析：
1）首先想到，将一列数字，两两交换，每次交换的结果都记录，交换到足够次数之后，就肯定能得到全排列的所有可能；
2）两个数的全排列肯定很简单吧，只需要交换一次就行了，那么三个数呢？不同的排列方式有 3！两两交换也不是很麻烦，那么更大的呢？
3）这时候我们想到递归可以将大问题分成n个小问题来解决
4）用代码来表示就是：for循环+交换+递归+交换
每次递归m+1，缩小带求排列的个数，for循环从m（i = m）开始，将第i个数与第m个数交换；
注意递归完之后需要对之前交换的数字返回原来序列及再次交换一次，防止重复。
void Full_arrangement(m + 1, n,min, dest,min_path,citys)
{
int i;
if (m == n)
{
for (i = 0; i < n - 1; i++)
printf("%d ", dest[i]);
printf("%d\n", dest[i]);
}
else
{
//该方法初始化dest数组与之前方法不同，需要将其初始化为全排列中的任意一个排列；
for (i = m; i < n; i++)
{
Swap(&dest[m],&dest[i]);
Full_arrangement(m + 1, n,min, dest,min_path,citys);
Swap(&dest[m],&dest[i]);
}
}
}详细代码请看上述函数：
void Full_arrangement(int m, int n, int* min, int* dest, int* tmp,int* min_path,int citys[5][5])
4. 计算比较 && 打印最短路径
计算比较并记录：
① 跟着之前的全排列，每次排列完一个可能（m == n），及将本次排列中两两城市的间隔距离计算⬇️
因为之前我们已经用 citys 数组存放过两两城市的间隔距离了，所以这里直接用for循环，将 dest 数组相邻两个数（城市）作为 citys 数组的横纵坐标，将距离加入变量 sum 中
② 之后再将变量 min 与 sum 比较大小，如果大于最小距离（这里先将 min 初始化为一个较大的数，并且需要传指针），则将本次总距离赋值到最小距离的变量（min）中，再将本次路径记录到 min_path 中
int sum = 0;
for (int i = 0; i < 4; i++)
{
sum += citys[dest[i]][dest[i + 1]];
}
if (sum < *min)
{
*min = sum;
for (int j = 0; j < 5; j++)
{
min_path[j] = dest[j];
}
}打印：
通过上述比较记录之后，min_path和min中已经存放的是最小路径和最短距离了，直接将其打印即可✔️
详细代码请看上述函数：void Printmin_path(int min,int* min_path)
生成exe文件https://blog.csdn.net/Dusong_/article/details/127750321?spm=1001.2014.3001.5502
summery
该题的递归确实很让人脑袋疼，需要反复咀嚼，通过自己的画图分析后，你会发现画图是真香啊
通过这次练习还需要习得大事化小的能力