【数据结构】快速排序

快速排序是一种高效的排序算法，其基本思想是分治法。它将一个大问题分解成若干个小问题进行解决，最后将这些解合并得到最终结果。

快速排序的主要思路如下：

1. 选择一个基准元素：从待排序的数组中选择一个元素作为基准（pivot）。通常选择第一个元素、最后一个元素或者随机选择一个元素作为基准。
2. 划分操作：将数组中的元素按照与基准的大小关系分成两部分，一部分小于基准，一部分大于基准。基准元素的选择决定了这个划分的位置。
3. 递归排序：对划分后的两个子数组分别进行快速排序，即递归地调用快速排序函数，直到子数组的大小为1或0时终止递归。
4. 合并结果：递归的终止条件是子数组的大小为1或0，此时子数组已经是有序的。然后将有序的子数组合并成一个有序的数组，整个排序过程完成。

快速排序的关键在于划分操作，通过每次划分将元素按照大小分开，使得在每次递归中，排序的元素数量逐渐减少，从而达到快速排序的效果。由于快速排序采用分治法，并且在平均情况下具有很好的时间复杂度（O(n log n)），因此它在实际应用中是一种较为常用的排序算法。然而，最坏情况下的时间复杂度为O(n^2)，这可以通过合理选择基准元素或采用随机化的方法进行优化。

实现步骤

首先设置一个数组，先找到最左侧和最右侧

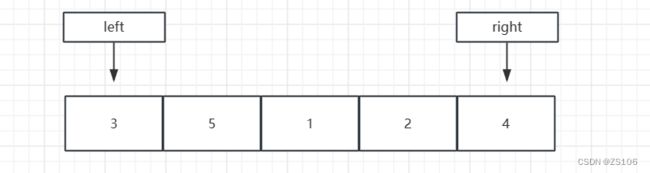
我们以left为pivot，如果比他大，就和right交换，right–，如果比pivot小，那么left和left+1交换，left++

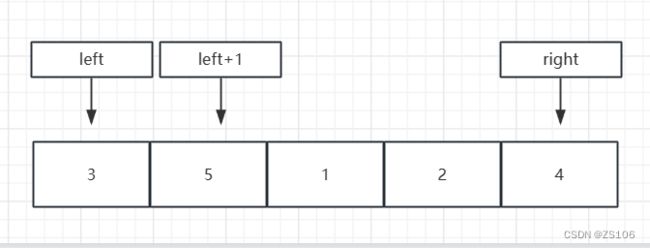
这里5>3,所以left+1与right交换，right–

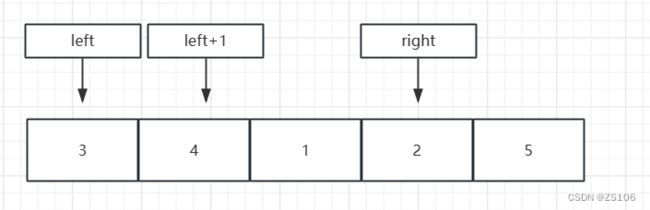
再次判断，4>3，所以接着与right交换

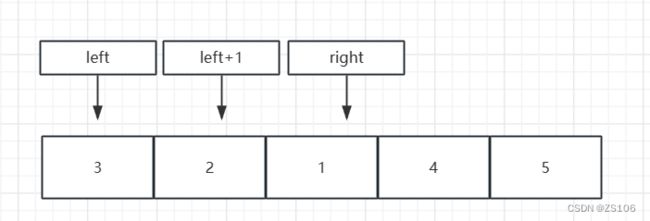
第三次判断 3>2 所以left和left+1交换，left++

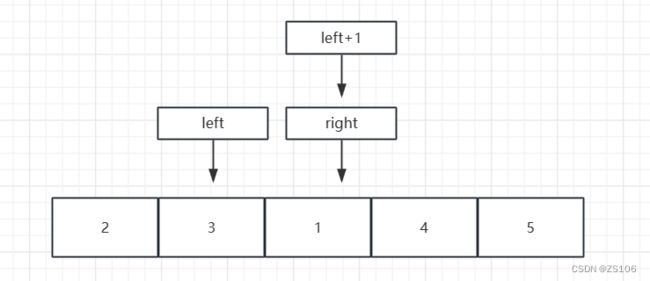
第四次判断，3>1,所以left和left+1交换，left++

这里可以看见left已经和right重合了，此时以3为pivot，左边全小于3，而右边全部大于3
这一个回合就完成了，而我们要做的就是如果左右的数组长度大于1，那么就拆分出来重新做上述的拆分，然后排序

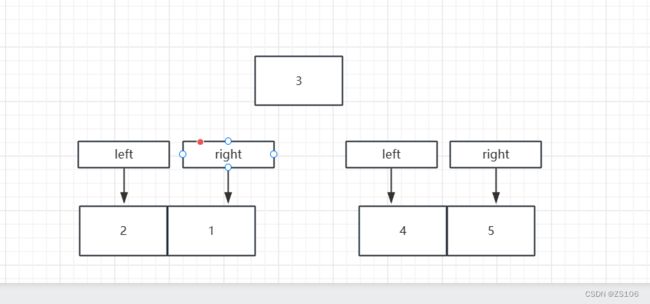
这就是快速排序的整体思路
下面给出快速排序的Java，C++，Python代码
Java:

public class QuickSort {
    public static void main(String[] args) {
        int[] arr = {153,134,153,14,196,4,616,435,156,1561,683,561,651,685,46,42};
        sort(0, arr.length-1,arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void sort(int left, int right,int[] array){
        int startIndex = left;
        int endIndex = right;

        while (left < right){
            if (array[left] >= array[left+1]){
                int temp = array[left];
                array[left] = array[left+1];
                array[left+1] = temp;
                left++;
            }else {
                int temp = array[left + 1];
                array[left + 1] = array[right];
                array[right] = temp;
                right--;
            }
        }

        if (left - startIndex -1 > 0){
            sort(startIndex,left-1,array);
        }
        if(endIndex - left - 1 > 0){
            sort(left+1,endIndex,array);
        }
    }
}

C++:

#include 
#include 

void quick_sort(std::vector<int>& array, int left, int right) {
    int startIndex = left;
    int endIndex = right;

    while (left < right) {
        if (array[left] >= array[left + 1]) {
            int temp = array[left];
            array[left] = array[left + 1];
            array[left + 1] = temp;
            left++;
        } else {
            int temp = array[left + 1];
            array[left + 1] = array[right];
            array[right] = temp;
            right--;
        }
    }

    if (left - startIndex - 1 > 0) {
        quick_sort(array, startIndex, left - 1);
    }
    if (endIndex - left - 1 > 0) {
        quick_sort(array, left + 1, endIndex);
    }
}

int main() {
    std::vector<int> arr = {153, 134, 153, 14, 196, 4, 616, 435, 156, 1561, 683, 561, 651, 685, 46, 42};
    quick_sort(arr, 0, arr.size() - 1);

    for (int i = 0; i < arr.size(); i++) {
        std::cout << arr[i] << " ";
    }
    std::cout << std::endl;

    return 0;
}

Python:

def quick_sort(array):
    if len(array) <= 1:
        return array

    pivot = array[0]
    left = [x for x in array[1:] if x <= pivot]
    right = [x for x in array[1:] if x > pivot]

    return quick_sort(left) + [pivot] + quick_sort(right)

arr = [153, 134, 153, 14, 196, 4, 616, 435, 156, 1561, 683, 561, 651, 685, 46, 42]
sorted_arr = quick_sort(arr)
print(sorted_arr)