分布式协议与算法——拜占庭将军问题
拜占庭将军问题
背景:以战国时期为背景
战国时期,齐、楚、燕、韩、赵、魏、秦七雄并立,后来秦国的势力不断强大起来,成了东方六国的共同威胁。于是,这六个国家决定联合,全力抗秦,免得被秦国各个击破。一天,苏秦作为合纵长,挂六国相印,带着六国的军队叩关函谷,驻军在了秦国边境,为围攻秦国作准备。但是,因为各国军队分别驻扎在秦国边境的不同地方,所以军队之间只能通过信使互相联系,这时,苏秦面临了一个很严峻的问题:如何统一大家的作战计划?
万一一些诸侯国在暗通秦国,发送误导性的作战信息,怎么办?如果信使被敌人截杀,甚至被敌人间谍替换,又该怎么办?这些都会导致自己的作战计划被扰乱,然后出现有的诸侯国在进攻,有的诸侯国在撤退的情况,而这时,秦国一定会趁机出兵,把他们逐一击破的。
问题:二忠一叛的难题
现有三个国家攻打秦国,分别叫齐、楚、燕。同时,又因为秦国很强大,所以只有半数以上的将军参与进攻,才能击败敌人。此时,将军们需要通过信使传递消息,然后协商一致之后,才能在同一时间发动进攻。
正常的情况:
例如:
- 齐根据侦查情况决定撤退。
- 楚和燕根据侦查信息,决定进攻。
这样最终进攻和撤退的二者的占比为2:1,因此最终会执行进攻的命令。
不正常的情况,存在叛军(恶意节点):
假设齐和燕为忠诚将军,楚为叛将。现在齐决定撤退、燕决定进攻。而由于楚已经叛变,他向齐传达“撤退”的命令,向燕传达“进攻”的命令。因此齐看到的结果为:进攻:撤退 = 1:2;燕看到的结果为:进攻:撤退 = 2:1。最终就燕自己去进攻秦军了,被灭了。
解决方法一:口信消息型拜占庭问题之解
三位将军分拨一部分军队,由苏秦带领。这样3位将军的作战讨论,变成了4位将军的作战讨论,这样可以增加讨论中忠诚将军的数量。
然后,四位将军约定了,如果没有收到命令,就执行预设的默认命令,例如撤退。需要进行多轮作战信息协商(协商的轮次与叛将的数量有关):
第一轮:
- 先发送作战信息的将军作为指挥官,其他的将军作为副官;
- 指挥官将他的作战信息发送给每位副官;
- 每位副官,将从指挥官处收到的作战信息,作为他的作战指令;如果没有收到作战信息,将把默认的“撤退”作为作战指令。
第二轮:
- 除了第一轮的指挥官外,剩余的 3 位将军将分别作为指挥官,向另外 2 位将军发送作战信息;
- 然后,这 3 位将军按照“少数服从多数”,执行收到的作战指令。
如果这里需要协商多轮,那么除了前面几轮的指挥官外,剩余的将军作为指挥官将作战信息发送每位副官。
具体协商过程:
分别以忠诚将军和叛将先发送作战信息为例:
1、忠诚将军先发送作战信息:
假设忠将苏秦先发送作战信息,作战指令是“进攻”。那么在第一轮作战协商中,苏秦向齐、楚、燕发送作战指令“进攻”,意味着齐、楚、燕分别收到了“进攻”的信息,并作为自己的作战指令。

在第二轮作战信息协商中,齐、楚、燕分别作为指挥官,分别向另外两位(第一轮指挥官苏秦除外)发送作战信息“进攻”。由于楚已经叛变,他为了干扰作战计划,向另外两位将军发送了“撤退”作战命令。
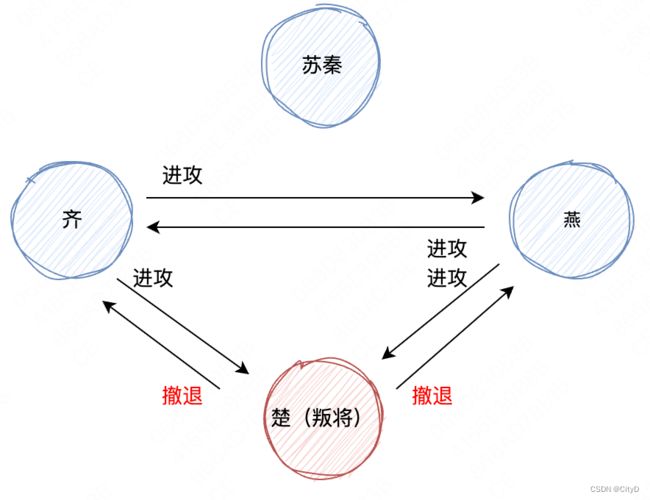
最终,齐和燕收到的作战信息都是“进攻、进攻、撤退”。按照少数服从多数的原则,执行“进攻”指令,实现了作战计划的一致性。
2、叛将先发送作战信息:
当叛将先发送作战消息,干扰作战计划时。在第一轮协商中,楚向苏秦发送“进攻作战指令”,向齐、燕发送“撤退”作战指令。苏秦、齐、燕收到后并将其作为自己的作战指令。

在第二轮作战信息协商中,苏秦、齐、燕分别作为指挥官,向另外两位发送作战信息。
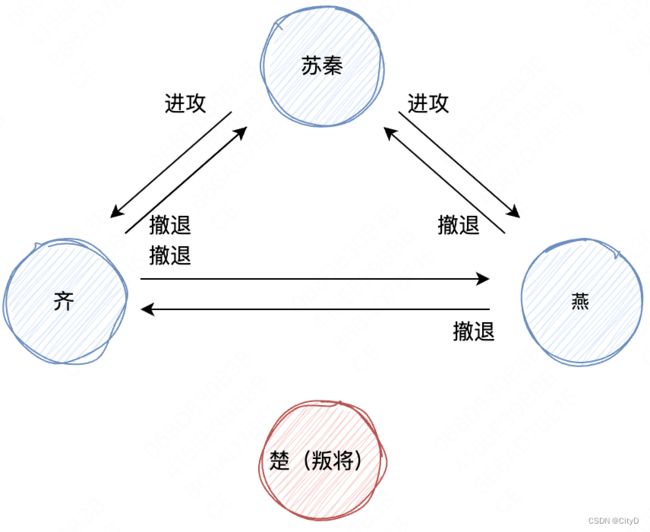
最终苏秦、齐、燕收到的信息都是“撤退、撤退、进攻”,按照少数服从多数的原则,执行“撤退”指令,实现了作战计划的一致性。
这个算法的前提:
- 如果叛将人数为m,将军人数不能少于3m+1(也就是:n位将军,最多能容忍(n-1)/3 位叛将)。
- 叛将数m决定递归循环的次数(进行多少轮作战信息协商),即m+1轮。
二忠一叛问题中,在存在1位叛将的情况下,必须增加1位将军。那么有没有办法在不增加将军人数的时候,直接解决二忠一叛的难题?可以通过签名消息型拜占庭问题之解进行解决。
解决办法二:签名消息型拜占庭问题之解
还可以通过签名的方式,在不增加将军人数的情况下,解决二忠一叛的难题。签名具有如下的特性:
- 忠诚将军的签名无法伪造,而且对他签名消息的内容进行任何更改都会被发现;
- 任何人都能验证将军签名的真伪。
与口信消息型拜占庭问题之解类似,签名消息型拜占庭问题之解同样需要多轮协商。协商的过程也与口信消息型拜占庭问题之解类似,但最终执行作战计划时并不是使用少数服从多数的原则。下面同样以忠诚将军和叛将分别先发送消息为例。
忠诚将军先发送消息
第一轮协商中,忠诚将军齐分别向楚和燕发送“进攻”的作战信息,燕和楚收到进攻的作战信息后将其作为自己的作战消息。

第二轮协商中,楚和燕分别作为指挥官分别向另一位将军(第一轮将军除外)发送作战信息。叛将楚修改或伪造作战信息,将“撤退”信息发送给了燕。那么燕在收到楚的作战信息的时候,会发现齐的作战信息被修改,楚已经叛变,这是燕会忽视来自楚的作战信息,最终执行齐发送的作战信息。

叛将先发送消息
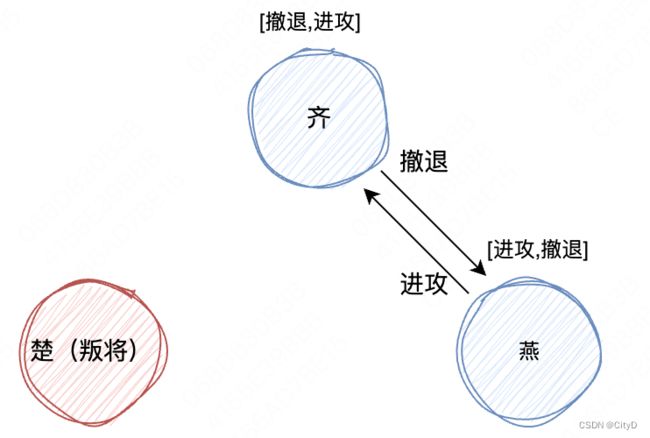
第一轮协商中,叛将楚向齐发送“撤退”的作战消息,向燕发送“进攻”的作战消息。

第二轮协商中,燕和齐分别作为指挥官分别向另一位将军(第一轮将军除外)发送作战信息。此时齐收到了[撤退、进攻]两个作战消息,燕收到了[进攻、撤退]两个作战消息。但是齐和燕会按照一定的规则在排序后的所有已接受的指令中选取一个(例如按照排序规则后的作战顺序为[进攻,撤退],都选择第一个作战计划)作战计划进行执行。最终执行一致的作战计划。
齐、燕收到的信息列表是内容是一样的,只是顺序不一样,使用相同的排序算法,选取策略,可以保证选取的指令时一样的
这个算法的前提是:
1、n位将军,最多允许 (n-2)位叛将。
2、同样需要多轮协商,如果叛将数位m,那么需要m + 1轮协商。
那如何实现签名消息呢?
可以使用非对称加密算法(如RSA),发送方使用哈希算法(如MD5)进行摘要,然后使用私钥对摘要进行加密,生成数字签名。然后将加密摘要和消息一起发送给接受方。接受方收到消息和加密摘要后,会用公钥对加密摘要进行解密,并对消息内容进行摘要,将两个摘要进行对比,以判断消息是否被篡改。
私钥加密,公钥解密。可以保证消息不会被冒充,因为私钥是不可泄漏的。如果公钥能正常解密出私钥加密的内容,就能证明这个消息是来源于持有私钥身份的人发送的。
感觉使用签名消息型拜占庭问题之解会更消耗算力一点。
小结
将将军作战中的场景与计算机世界的分布式场景进行对应:
- 故事里的将军,可以理解为计算机节点。
- 忠诚将军,可以理解为正常运行的计算机节点。
- 叛变将军,可以理解为出现故障并会发送误导信息的计算机节点。
- 信使被杀,可以理解为通讯故障、信息丢失。
- 信使被间谍替换,可以理解为通讯被中间人攻击,攻击者在恶意伪造信息和劫持通讯。
拜占庭将军问描述的是最困难的,也是最复杂的一种分布式故障场景,除了存在故障行为,还存在恶意行为的场景。因此在存在恶意行为的场景中(如数字货币的区块链技术中),必须使用拜占庭容错算法(Byzantine Fault Tolerance,BFT)。除了上面提到的两种算法(口信消息型拜占庭问题之解、签名消息型拜占庭问题之解),常用的拜占庭容错算法还有:PBFT算法,PoW算法。
在计算机分布式系统中,最常用的是非拜占庭容错算法,即故障容错算法(Crash Fault Tolerance,CFT)。CFT 解决的是分布式的系统中存在故障,但不存在恶意节点的场景下的共识问题。 也就是说,这个场景可能会丢失消息,或者有消息重复,但不存在错误消息,或者伪造消息的情况。常见的算法有 Paxos 算法、Raft 算法、ZAB 协议。
参考
- 分布式协议与算法实战 学习笔记