二叉搜索树讲解及其C++代码实现

文章概述：本文介绍了二叉搜索树的概念、一般操作和其C++代码实现。不是很了解二叉搜索树请先看教材和讲解然后参照代码自己动手试一试；如果只是需要实现代码&测试代码，请直接查看第四节。

参考教材：清华大学《数据结构》第2版教材（殷人昆主编）
编程语言：C++

一、二叉搜索树的概念

二叉搜索树（Binary search tree）或者是一颗空树，或者是具有下列性质的二叉树：
（1）每个结点都有一个作为搜索依据的关键码（key），所有结点的关键码互不相同。
（2）左子树（如果存在）上所有结点的关键码都小于根结点的关键码。
（3）右子树（如果存在）上所有结点的关键码都大于根结点的关键码。
（4）左子树和右子树也是二叉搜索树。
下面是二叉搜索树的一些例子：

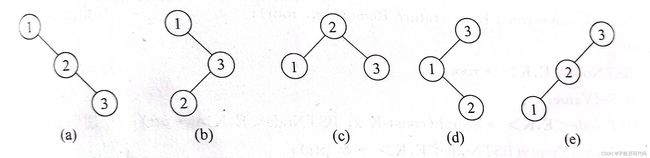
二、二叉搜索树的基本操作

2.1 二叉搜索树上的搜索

在二叉搜索树上进行搜索，是一个从根结点开始，沿某一个分支逐层向下进行比较判等的过长，它可以是一个递归的过程。假设想要在二叉搜索树中搜索关键码为$x$的元素，搜索过程从根节点开始。如果根指针为NULL，则搜索不成功；否则用给定的值$x$与根结点的关键码进行比较：

• 如果给定值等于根结点的关键码，则搜索成功，返回搜索成功信息。
• 如果给定值小于根结点的关键码，则继续递归搜索根结点的左子树。
• 否则（大于），递归搜索根结点的右子树。

下面给出一个在二叉搜索树中进行搜索的例子：

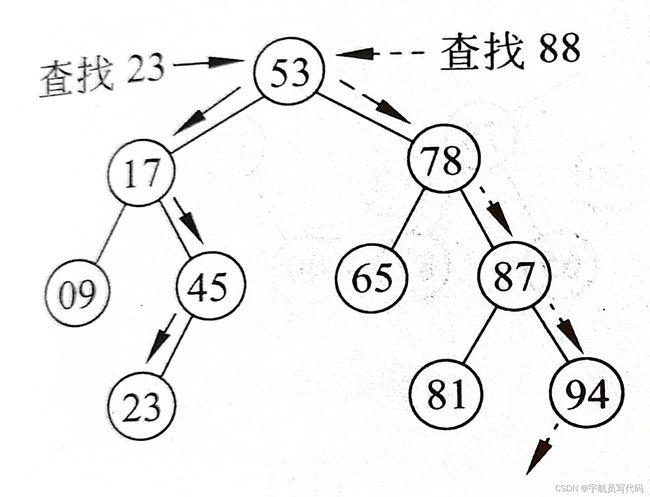
上图中查找到了23，但没找到88。可以看到，若设二叉搜索树的高度为h，则比较次数不超过h。

2.2 二叉搜索树的插入

为了向二叉搜索树中插入一个元素，必须先检查这个元素是否在树中已经存在。所以在插入之前，先使用搜索算法在树中检查要插入元素有还是没有。如果搜索成功，说明树中已经有这个元素，不再插入；如果搜索不成功，说明树中原来没有关键码等于给定值的结点，把新元素加到搜索操作停止的地方。一个插入的例子如下图所示：

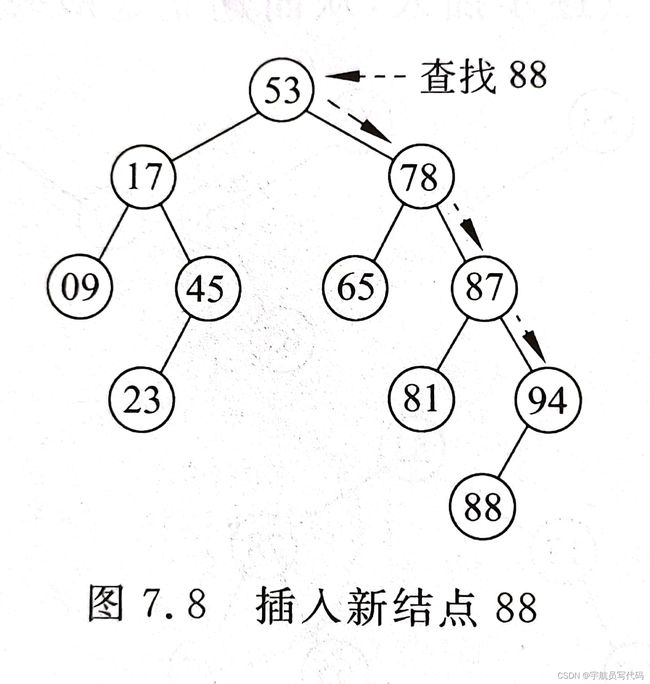
2.3 二叉搜索树的删除

在二叉搜索树中删除一个结点时，必须将因删除结点而断开的二叉链表重新链接起来，同时确保二叉搜索树的性质不会失去。此外，为了保证在执行删除后，树的搜索性能不至于降低，还需要防止重新链接后树的高度不能增加。在删除时这些因素都应该被体现。

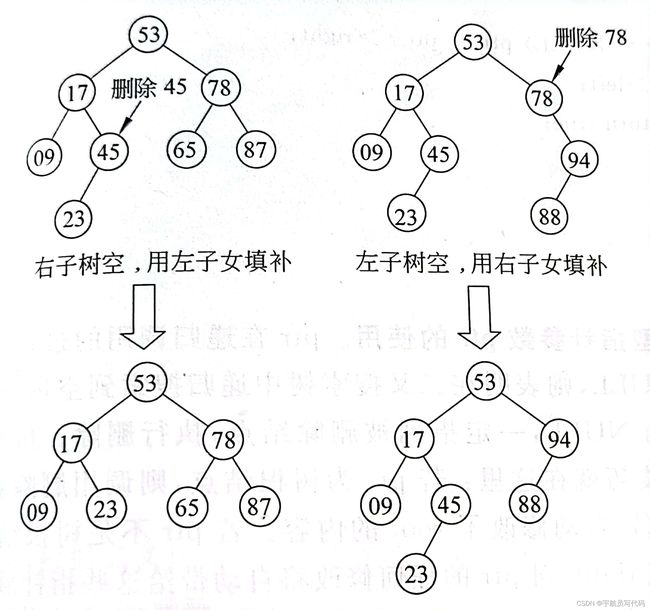
• 如果想要删除叶结点，只需将其父结点指向它的指针清零，再释放它即可。如果被删除结点右子树为空，则可以拿它的左子女结点顶替它的位置，再释放它；如果被删结点左子树为空，可以拿它的右子女结点顶替它的位置，再释放它。
  
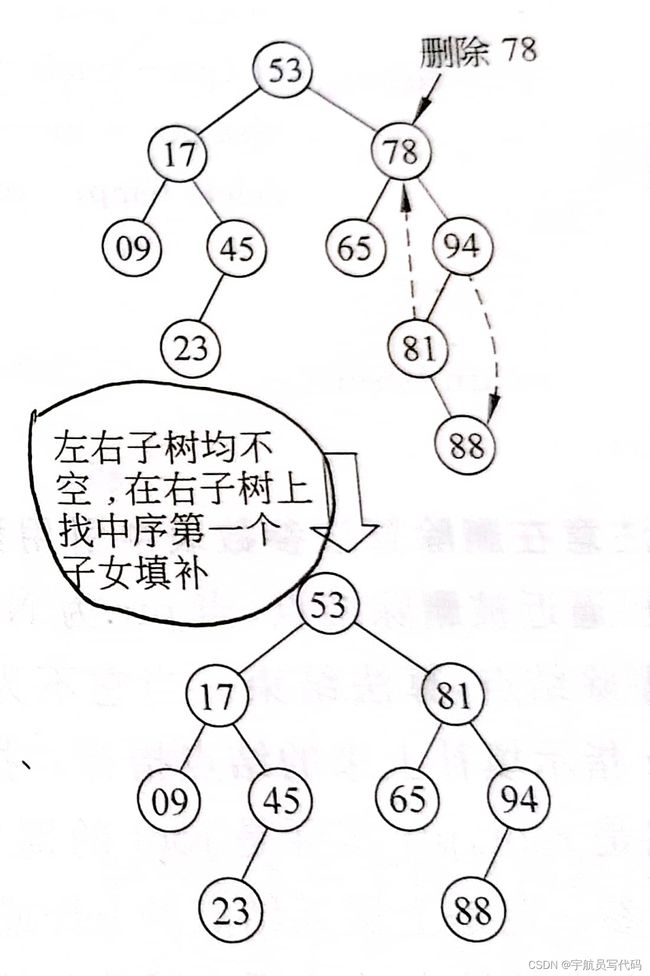
• 如果被删结点的左、右子树都不空，可以在它的右子树中寻找中序下的第一个结点（关键码最小），用它的值填补到被删结点中，再来处理这个结点的删除问题。当然也可以在被删结点的左子树中找到中序下的最后一个结点（关键码最大），用它来填补被删结点。
  

三、二叉搜索树的一些其他相关操作

这部分内容是为了完善二叉搜索树功能而讲解。

3.1 二叉搜索树取最大元素和最小元素

由二叉搜索树性质知道：递归取二叉搜索树的**左子树（左下角结点）便得到了树中所有元素的最小元素；递归取二叉搜索树的右子树（右下角结点）**便得到了树中所有元素的最小元素；

如上图，最小值为左下角结点09，最大值为右下角结点94。

3.2 二叉树的序列化

将一棵二叉搜索树中序遍历，并记录遍历过程中的数据，便得到二叉搜索树中所有元素的升序排列。（相当于不断地取最小）
如3.1节图，前序遍历该搜索二叉树，得到序列：09 17 23 45 53 65 78 81 87 88 94即为所有元素的一个升序排列。

3.3 打印搜索二叉树

可以采取前序遍历的做法，每个结点占一行，并记录当前结点层数进行打印。（把整个二叉树“横过来”）算法伪代码如下：

//level的初值为-1
PrintTree(ptr,level):
if ptr == nullptr then:
	return;
level ++;
PrintTree(ptr->right,level);
level --;

level ++;
for (int i = 0; i < level; i++)
        cout << "\t";//打印分隔符表明层数
cout << ptr->data << endl;
PrintTree(ptr->left, level);
level--;

3.4 二叉搜索树的删除

采取中序遍历的方法，递归删除结点即可。

四、C++实现二叉搜索树代码

4.1 对教材伪代码框架的改动说明

1. 与原版教材不同的是，我这里使用模板时省去了关键字key，因为我认为进行比较时，对于一般的数据类型（如int,double,char）等，键值即它本身；而对于结构体类型，完全可以重载它的比较函数，自定义比较键值。
2. 另外添加了size成员变量及其方法获取树中元素个数。
3. 添加了GetSeq函数获取二叉搜索树的序列化。

4.2 代码实现

#include 
#include 
using namespace std;
template <class E>
struct BSTNode
{
    E data;
    BSTNode<E> *left, *right;
    BSTNode() : left(nullptr), right(nullptr) {}
    BSTNode(const E d, BSTNode<E> *L = nullptr, BSTNode<E> *R = nullptr) : data(d), left(L), right(R) {}
    ~BSTNode() {}
    void setData(E d) { data = d; }
    E getData() { return data; }
};

template <class E>
class BST
{
public:
    BST() : root(nullptr), size(0) {}
    BST(const BST<E> &R);
    BST(E *Eles, size_t sz);
    ~BST() { makeEmpty(); };
    size_t Size() { return size; }
    bool Search(const E x) const
    {
        return (Search(x, root) != nullptr) ? true : false;
    }
    BST<E> &operator=(const BST<E> &R);
    void makeEmpty()
    {
        makeEmpty(root);
        root = nullptr;
        size = 0;
    }
    void PrintTree()
    {
        int level = -1;
        PrintTree(root, level);
    };
    E Min()
    {
        if (root == nullptr)
        {
            cerr << "BST is empty." << endl;
            exit(-1);
        }
        return Min(root)->data;
    }
    E Max()
    {
        if (root == nullptr)
        {
            cerr << "BST is empty." << endl;
            exit(-1);
        }
        return Max(root)->data;
    }
    bool Insert(const E &el) { return Insert(el, root); }
    bool Remove(const E x) { return Remove(x, root); }
    E *GetSeq(); //将二叉搜索树中所有结点按升序排列，返回到seq中
private:
    size_t size;
    BSTNode<E> *root;                                     //二叉搜索树根节点                                      //输入停止标志，用于输入
    BSTNode<E> *Search(const E x, BSTNode<E> *ptr) const; //递归：搜索
    void makeEmpty(BSTNode<E> *&ptr);                     //递归：置空
    void PrintTree(BSTNode<E> *ptr, int level) const;     //递归：打印
    BSTNode<E> *Copy(const BSTNode<E> *ptr) const;        //递归：复制
    BSTNode<E> *Min(BSTNode<E> *ptr) const;               //递归：求最小
    BSTNode<E> *Max(BSTNode<E> *ptr) const;               //递归：求最大
    bool Insert(const E &el, BSTNode<E> *&ptr);           //递归：插入
    bool Remove(const E x, BSTNode<E> *&ptr);             //递归：删除
    void GetSeq(E *x, int &cnt, BSTNode<E> *&ptr);
};

//建立二叉搜索树
template <class E>
BST<E>::BST(E *Eles, size_t sz)
{
    //输入一个元素序列，建立一棵二叉搜索树
    E x;
    root = nullptr;
    size = 0;
    for (int i = 0; i < sz; i++)
    {
        x = Eles[i];
        Insert(x, root);
    }
}

template <class E>
BSTNode<E> *BST<E>::Search(const E x, BSTNode<E> *ptr) const
{
    //私有递归函数，在以ptr为根的二叉搜索树中搜索含x的结点。若找到，则函数返回该结点的地址，否则返回nullptr。
    if (ptr == nullptr)
        return nullptr;
    else if (x < ptr->data)
        return Search(x, ptr->left);
    else if (x > ptr->data)
        return Search(x, ptr->right);
    else
        return ptr;
}

template <class E>
bool BST<E>::Insert(const E &el, BSTNode<E> *&ptr)
{
    if (ptr == nullptr)
    {
        ptr = new BSTNode<E>(el);
        if (ptr == nullptr)
        {
            cerr << "Out of space." << endl;
            exit(-1);
        }
        size += 1;
        return true;
    }
    else if (el < ptr->data)
        return Insert(el, ptr->left);
    else if (el > ptr->data)
        return Insert(el, ptr->right);
    else
        return false; //值相等，插入失败
    return true;
}

template <class E>
bool BST<E>::Remove(const E x, BSTNode<E> *&ptr)
{
    BSTNode<E> *temp;
    if (ptr != nullptr)
    {
        if (x < ptr->data)
            Remove(x, ptr->left);
        else if (x > ptr->data)
            Remove(x, ptr->right);
        else if (ptr->left != nullptr && ptr->right != nullptr)
        {
            temp = ptr->right;
            while (temp->left != nullptr)
                temp = temp->left;
            ptr->data = temp->data;
            Remove(ptr->data, ptr->right);
        }
        else
        {
            temp = ptr;
            if (ptr->left == nullptr)
                ptr = ptr->right;
            else
                ptr = ptr->left;
            delete temp;
            size -= 1;
            return true;
        }
    }
    return false;
}

template <class E>
void BST<E>::makeEmpty(BSTNode<E> *&ptr)
{
    if (ptr == nullptr)
        return;
    if (ptr->left != nullptr)
    {
        makeEmpty(ptr->left);
    }
    else if (ptr->right != nullptr)
    {
        makeEmpty(ptr->right);
    }
    delete ptr;
    ptr = nullptr;
    return;
}

template <class E>
void BST<E>::PrintTree(BSTNode<E> *ptr, int level) const
{
    if (ptr == nullptr)
    {
        return;
    }

    level++;
    PrintTree(ptr->right, level);
    level--;

    level++;
    for (int i = 0; i < level; i++)
        cout << "\t";
    cout << ptr->data << endl;
    PrintTree(ptr->left, level);
    level--;
}

template <class E>
BST<E>::BST(const BST<E> &R)
{
    if (this != &R)
    {
        this->root = R.Copy(R.root);
        this->size = R.size;
    }
}
template <class E>
BST<E> &BST<E>::operator=(const BST<E> &R)
{
    if (this != &R)
    {
        this->makeEmpty(); //防止内存泄漏，先释放原来的空间
        this->root = R.Copy(R.root);
        this->size = R.size;
    }
    return *this;
}
template <class E>
BSTNode<E> *BST<E>::Copy(const BSTNode<E> *ptr) const
{
    if (ptr == nullptr)
        return nullptr;
    BSTNode<E> *ret = new BSTNode<E>(ptr->data);
    ret->left = Copy(ptr->left);
    ret->right = Copy(ptr->right);
    return ret;
}

template <class E>
BSTNode<E> *BST<E>::Min(BSTNode<E> *ptr) const
{
    if (ptr->left != nullptr)
        return Min(ptr->left);
    return ptr;
}

template <class E>
BSTNode<E> *BST<E>::Max(BSTNode<E> *ptr) const
{
    if (ptr->right != nullptr)
        return Max(ptr->right);
    return ptr;
}

template <class E>
E *BST<E>::GetSeq()
{
    E *seq = new E(size);
    int cnt = 0;
    GetSeq(seq, cnt, root);
    return seq;
}

template <class E>
void BST<E>::GetSeq(E *x, int &cnt, BSTNode<E> *&ptr)
{
    if (ptr == nullptr || cnt >= size)
        return;
    GetSeq(x, cnt, ptr->left);
    E e = ptr->data;
    x[cnt] = e;
    cnt++;
    GetSeq(x, cnt, ptr->right);
}

原理已经在上面的讲解中说明清楚了，如果有看不懂的地方，请参照教材和图例，或者在评论区提问。

4.3 使用及测试代码

为了检验实现的正确性，我实现了一些检测功能的demo函数：

//需要包含头文件"assert.h"
void Test_Init()
{
    int a[5] = {1, 2, 3, 4, 5};
    BST<int> bst(a, 5);
    assert(bst.Size() == 5);
    cout << "Test_Init passed." << endl;
}

void Test_Insert()
{
    BST<int> bst;
    for (int i = 0; i <= 10; i += 2)
        bst.Insert(i);
    for (int i = 1; i <= 9; i += 2)
        bst.Insert(i);

    bst.Insert(9); //插入已经存在的元素应该失败
    assert(bst.Size() == 11);
    cout << "Test_Insert passed." << endl;
}

void Test_Remove()
{
    BST<int> bst;
    for (int i = 0; i < 10; i++)
        bst.Insert(i);
    assert(bst.Size() == 10);
    bst.Remove(11); //删除不存在的元素应该失败
    assert(bst.Size() == 10);
    for (int i = 0; i < 10; i++)
    {
        bst.Remove(i);
        assert(bst.Size() == 9 - i);
    }
    cout << "Test_Remove passed." << endl;
}

void Test_Print()
{
    BST<int> bst;
    bst.Insert(3);
    bst.Insert(2);
    bst.Insert(4);
    bst.PrintTree();
    cout << "Test_Print passed." << endl;
}

void Test_Seq()
{
    BST<int> bst;
    bst.Insert(3);
    bst.Insert(5);
    bst.Insert(1);
    bst.Insert(4);
    bst.Insert(2);
    bst.Insert(0);

    int *seq = bst.GetSeq();
    for (int i = 0; i < bst.Size(); i++)
        assert(seq[i] == i);
    cout << "Test_Seq passed." << endl;
}

void Test_Min_Max()
{
    BST<int> bst;
    bst.Insert(3);
    bst.Insert(5);
    bst.Insert(1);
    bst.Insert(4);
    bst.Insert(2);
    bst.Insert(0);

    assert(bst.Max() == 5);
    assert(bst.Min() == 0);
    cout << "Test_Min_Max passed." << endl;
}

void Test_Copy()
{
    BST<int> bst;
    bst.Insert(1);
    bst.Insert(0);
    bst.Insert(2);

    BST<int> bst2 = bst; //拷贝构造函数
    assert(bst2.Size() == bst.Size());
    int *seq2 = bst2.GetSeq();
    for (int i = 0; i < 3; i++)
        assert(seq2[i] == i);

    BST<int> bst3; //赋值重载函数
    bst3 = bst;
    assert(bst3.Size() == bst.Size());
    int *seq3 = bst3.GetSeq();
    for (int i = 0; i < 3; i++)
        assert(seq3[i] == i);

    cout << "Test_Copy passed." << endl;
}

void Test_Empty()
{
    BST<int> bst;
    bst.Insert(1);
    bst.Insert(0);
    bst.Insert(2);
    assert(bst.Size() == 3);

    bst.makeEmpty();
    assert(bst.Size() == 0);

    for (int i = 0; i < 3; i++)
    {
        bst.Insert(i);
        assert(bst.Size() == i + 1);
    }

    cout << "Test_Empty passed." << endl;
}

void Test_All()
{
    Test_Init();
    Test_Insert();
    Test_Remove();
    Test_Print();
    Test_Seq();
    Test_Copy();
    Test_Min_Max();
    Test_Empty();

    cout << "All Test Passed." << endl;
}
int main()
{
    Test_All();
}

运行效果：

大家可以先大致看下讲解（如果不懂的话），然后根据需求自取代码。