【习题】几道二叉树题目，进来看看你会不？
几道二叉树题目解析
- 前言
- 正式开始
-
- 1. 根据二叉树创建字符串（力扣606）
-
- 题目描述
- 解析
- 代码
- 2. 二叉树的层序遍历1（力扣102）
-
- 题目描述
- 解析
- 代码
- 3. 二叉树的层序遍历2（力扣107）
-
- 代码
- 4. 二叉树的最近公共祖先（力扣236）
-
- 题目描述
- 解析
-
- 解法一
- 解法二
- 代码
-
- find查找解法
- 双栈解法
- 本题的一点拓展
-
- 如果该树是一棵二叉搜索树
- 如果该树结构为三叉链
- 5. 二叉搜索树与双向链表（牛客JZ36）
-
- 题目描述
- 解析
- 代码
- 6. 从前序与中序遍历序列构造二叉树（力扣105）
-
- 题目描述
- 解析
- 代码
- 7. 从中序与后序遍历序列构造二叉树（力扣106）
-
- 题目描述
- 解析
- 代码
- 8. 非递归实现二叉树的前序遍历（力扣144）
-
- 题目描述
- 解析
- 代码
- 9. 非递归实现二叉树的中序遍历（力扣94）
-
- 题目描述
- 解析
- 代码
- 10. 非递归实现二叉树的后序遍历（力扣145）
-
- 题目描述
- 解析
- 代码
前言
这里给出如下题目，各位可以先点击链接看看你是否会做：
- 根据二叉树创建字符串（力扣606）
- 二叉树的层序遍历1（力扣102）
- 二叉树的层序遍历2（力扣107）
- 二叉树的最近公共祖先（力扣236）
- 二叉搜索树与双向链表（牛客JZ36）
- 从前序与中序遍历序列构造二叉树（力扣105）
- 从中序与后序遍历序列构造二叉树（力扣106）
- 非递归实现二叉树的前序遍历（力扣144）
- 非递归实现二叉树的中序遍历（力扣94）
- 非递归实现二叉树的后序遍历（力扣145）
如果上面这些题不是全会的话，建议看看我的解析，我尽量讲的详细一点。
如果上面这些题都会的话，也可以看看我的解析，看看你的做法和我的做法都一样不。
那么下面就挨着讲。
正式开始
每道题都是先给题目描述，然后给解析，最后给代码。
1. 根据二叉树创建字符串（力扣606）
题目描述
题目想让我们将二叉树的每个节点的根和左子树右子树建立一一对应的关系，并将这些关系用括号表示，并最终以字符串的形式返回。
并不是所有的左右节点都需要加括号，分情况：
- 左右子树的根节点都不为空时，二者都需要加括号。
- 左子树根节点为空，右子树根节点不为空时，二者都需要加括号。
- 左子树根节点不为空，右子树根节点为空时，不需要给右边加括号。
- 左右子树根节点都为空时，不需要给二者加括号。
解释一下第二点，当左为空右不为空时，如果给左括号省略了，就不能判断出左右节点的位置了。
比如：
解析
题目中的示例其实也提示了，我们可以先都加上括号，然后分情况省略掉不需要加括号的：
总结一下上面的四种情况，省略掉括号的应该是如下情况：
- 左右都为空，省略掉左右的括号
- 左不为空右为空，省略掉右括号
那么想要先都加上括号的话，就可写出如下代码：
不断递归就能得到都加上括号的字符串。
然后我们再来省略不需要加括号的情况，也就是需要留下括号的情况，再总结下上面的总结：
- 当 左不为空 或者 左为空且右不为空 时，左括号就要留下。
- 当 右不为空 时，右括号就要留下。
故可写出如下代码：
代码
class Solution {
public:
string tree2str(TreeNode* root) {
if(root == nullptr)
return string();
string res;
res += to_string(root->val);
if(root->left || (root->left == nullptr && root->right))
{
res += '(';
res += tree2str(root->left);
res += ')';
}
if(root->right)
{
res += '(';
res += tree2str(root->right);
res += ')';
}
return res;
}
};
2. 二叉树的层序遍历1（力扣102）
题目描述
本题需要我们将二叉树的层序遍历中每一层的遍历结果放到数组中。
解析
如果是单纯的层序遍历的话，我们可以用队列来实现。
但是这里有了限制条件，需要我们将每层的遍历结果放到数组中。
我们就可仍然用队列来实现层序遍历，并通过限制条件来按层的遍历，控制队列由原来的一个一个的出变为一层一层的出。
这里给出图解方便理解：
那么就可写下如下代码：
代码
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> vv;
if(root == nullptr) // root为空，直接返回空数组
return vv;
queue<TreeNode*> q;
// 先入根节点
q.push(root);
// q不为空说明内部还有下一层的节点，需要继续遍历下一层
// q为空就是遍历完了
while(!q.empty())
{
// tmp用来记录每一层的节点
vector<int> tmp;
// sz表示每一层的节点个数，也就是要遍历几个节点
int sz = q.size();
while(sz--)
{
TreeNode* front = q.front();
q.pop();
// 记录每个节点
tmp.push_back(front->val);
// 左不为空，入队
if(front->left)
q.push(front->left);
// 右不为空，入队
if(front->right)
q.push(front->right);
}
// 将每一层记录
vv.push_back(tmp);
}
return vv;
}
};
其实这道题还可以用双队列，一个存放节点，一个存放每层的非空节点个数，然后通过控制第二个队列来控制第一个队列每次的出队个数，思想和刚刚的方法是一样的。这里就不写了，感兴趣的同学可以自己尝试写一写。
3. 二叉树的层序遍历2（力扣107）
本题和前面的那道题一样的，只不过是让存储的数组顺序变一下。
那我们直接在最后用个reverse就好了，不需要再搞复杂了，直接给代码：
代码
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> vv;
if(root == nullptr) // root为空，直接返回空数组
return vv;
queue<TreeNode*> q;
// 先入根节点
q.push(root);
// q不为空说明内部还有下一层的节点，需要继续遍历下一层
// q为空就是遍历完了
while(!q.empty())
{
// tmp用来记录每一层的节点
vector<int> tmp;
// sz表示每一层的节点个数，也就是要遍历几个节点
int sz = q.size();
while(sz--)
{
TreeNode* front = q.front();
q.pop();
// 记录每个节点
tmp.push_back(front->val);
// 左不为空，入队
if(front->left)
q.push(front->left);
// 右不为空，入队
if(front->right)
q.push(front->right);
}
// 将每一层记录
vv.push_back(tmp);
}
// 翻转一下就好
reverse(vv.begin(), vv.end());
return vv;
}
};
4. 二叉树的最近公共祖先（力扣236）
这道题还是比较重要的，在剑指offer的最后的面试那块就提到了这道题。
题目描述
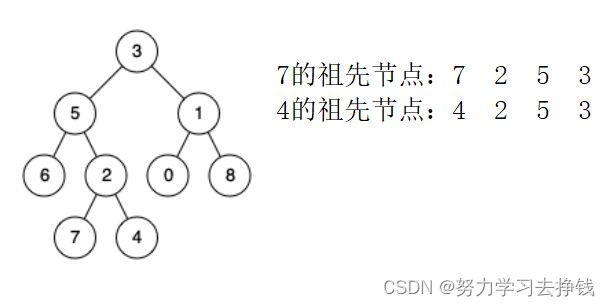
先说什么是祖先节点，就是从当前节点到根节点的所有节点都是其祖先节点。比如说：
这道题让我们求两个节点的最近公共祖先节点。就比如说上面的7和4，最近的公共祖先为2。
解析
题目中的二叉树就是一颗普通的二叉树，没有什么特殊的地方。
我们可以先来列举一些场景。
刚刚的7和4：
6和7
4和0
2和1
上面的都是一些普通场景，我们可以发现，最近的两个节点的最近祖先节点一定是在祖先节点的左右子树上。所以通过这一点就能做了。
但是还有特殊场景：
4和5
3和7
上面这种场景，当两个节点中的某一个是祖先节点的话，那么这个节点就是最近的祖先节点。
然后就没有什么特殊情况了，开始写代码，先用递归来写：
解法一
首先要写出查询节点的函数，用来查节点的左右子树：
然后再用findNode来实现找最近公共祖先。
解法二
用两个栈来存放路径。
先序遍历，一个栈存放从根到p的路径，一个栈存放从根到q的路径。
遍历到一个节点时，如果该节点为空，返回false，说明当前路径已经找到末尾。
如果不是空，先入栈。
然后再判断当前节点是否为要找的节点，如果是，直接返回true。
如果不是，递归判断其左，为真表明路径在左树中，并已经找到，返回true。
当左为空，递归判断其右，为真表明路径在右树中，并已经找到，返回true。
当左右都为空，就将其从栈中pop掉并返回false，表明当前路径已走完，需要换一条路径。
看图解：
此处即得到从根到p的路径，为3，5，6。
此处即得到从根到q的路径，即3，5，2，7。
所以p和q的路径都有了，找最近的公共祖先节点就更简单了，就类似于链表相交问题。
栈大的先pop两栈的大小差次，然后同时pop，直到二者栈顶元素相同。
写出如下代码。
先写一个用栈来记录路径的函数：
将p和q的路径找到，在栈中对比二者路径，直到找到最进祖先节点即可。
代码
find查找解法
class Solution {
public:
bool findNode(TreeNode* root, TreeNode* p)
{
if(root == nullptr)
return false;
return root == p
|| findNode(root->left, p)
|| findNode(root->right, p);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == nullptr)
return nullptr;
// p || q 一个为root，root就是最近祖先节点
if(root == p || root == q)
return root;
// p 在左树
bool pL = findNode(root->left, p);
bool pR = !pL;
// q 在左树
bool qL = findNode(root->left, q);
bool qR = !qL;
// 二者一左一右，当前节点为最近祖先节点
if((pL && qR) || (qL && pR))
return root;
// 都在左，去左树找
if(pL && qL)
return lowestCommonAncestor(root->left, p, q);
// 都在右，去右树找
if(pR && qR)
return lowestCommonAncestor(root->right, p, q);
return nullptr;
}
};
双栈解法
class Solution {
public:
bool roadRecord(TreeNode* root, TreeNode* node, stack<TreeNode*>& st)
{
// 当前节点为空，说明当前路径已经找到结尾
if(root == nullptr)
return false;
// 节点先入栈
st.push(root);
// 如果当前节点为要找的节点，就返回true，说明已经找到，即为当前节点
if(root == node)
return true;
// 当前节点未找到，去左树中找节点
// 左树中找到了，也即路径也找到了，返回true
if(roadRecord(root->left, node, st))
return true;
// 左树中未找到节点，去右树中找
// 右树中找到了，也即路径也找到了，返回true
if(roadRecord(root->right, node, st))
return true;
// 当前节点不是，左右树中都未找到，将栈顶元素pop掉，返回false
// 表示换一条路径
st.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack<TreeNode*> pRoad;
stack<TreeNode*> qRoad;
// 记录p和q的路径
roadRecord(root, p, pRoad);
roadRecord(root, q, qRoad);
// 让两栈大小相同
while(pRoad.size() > qRoad.size())
pRoad.pop();
while(qRoad.size() > pRoad.size())
qRoad.pop();
// 找到栈顶相同为止
while(pRoad.top() != qRoad.top())
{
pRoad.pop();
qRoad.pop();
}
// 返回任意一个栈的栈顶即可
return pRoad.top();
}
};
本题的一点拓展
如果说，我再往树中加点条件。
如果该树是一棵二叉搜索树
那么find那种解法就不需要再写find函数了。
直接根据二叉搜索树的特性，左<根<右，就可判断出节点是否在左树还是右树。
如果该树结构为三叉链
意思就是树节点中还有一个节点指向其父节点。
那么这道题做起来就更简单了，光用指向父节点的指针，直接可以做成链表相交的那道题。
5. 二叉搜索树与双向链表（牛客JZ36）
题目描述
本题让我们把一棵二叉搜索树转换为双向链表。注意是转换。
题目中有一个要求：我们不能创建新的节点。
那么想中序遍历二叉树然后一个一个new链表节点再push到后面的话，就不满足题目要求了。题目是想让我们使得原树节点左指向按照中序遍历顺序的当前节点前一个节点，右指向后一个节点。
解析
有什么好方法呢？
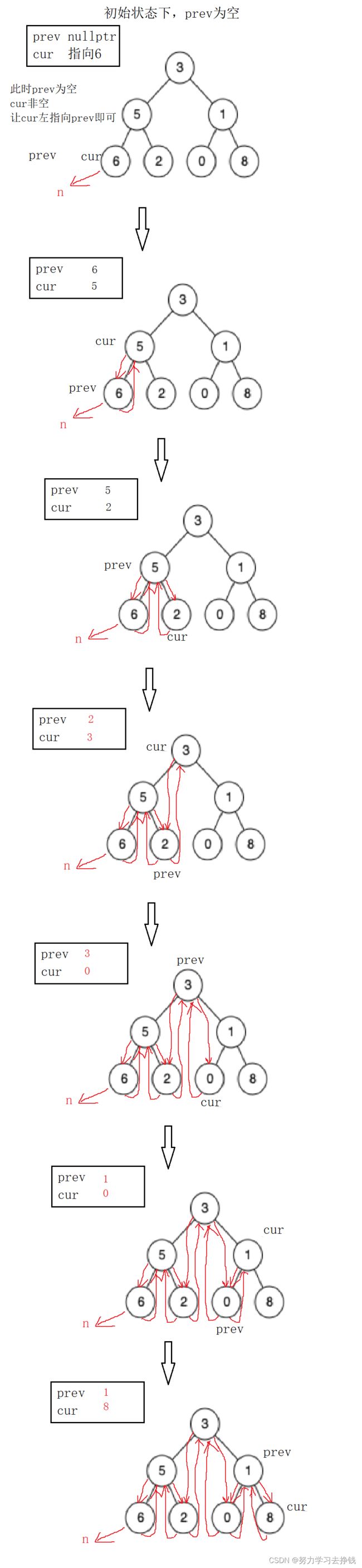
我们可以定义一个prev用来表示上一次遍历到的节点。
中序遍历，让当前节点的左指向prev，让prev的右指向当前节点，这样就解决了。但是要注意一下边界条件。
看看图解：
我们可以先写一个改变指针指向的函数（这段代码有问题，等会说）：
将二叉树转变为链表后再找到最左边的节点返回即可：
但是上面的代码出现了经典的问题，就是prev一直是传值，我所画的图中，prev只有一个。
但是上面的传值，会导致每一层调用的时候都是那一层初始情况下的值，不会影响其他递归调用的prev，所以就会导致有多个prev。
所以运行起来后就出错了。
我们可以在指针的后面加个引用，这样就能使得整个过程中只有一个prev了。
注意这里的prev相当于一个TreeNode*的别名。
代码
class Solution {
public:
void changePtr(TreeNode* root, TreeNode* prev)
{
if(root == nullptr)
return;
changePtr(root->left, prev);
root->left = prev;
if(prev)
prev->right = root;
prev = root;
changePtr(root->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree)
{
if(pRootOfTree == nullptr)
return nullptr;
TreeNode* prev = nullptr;
changePtr(pRootOfTree, prev);
TreeNode* cur = pRootOfTree;
while(cur->left)
cur = cur->left;
return cur;
}
};
6. 从前序与中序遍历序列构造二叉树（力扣105）
题目描述
本题中给了你二叉树的前序遍历和中序遍历的顺序，并存放在了数组中，让你通过这两个数组还原出对应的二叉树。
解析
这道题解法很像一道题，那道题大概就是给你一段字符串让你用这个字符串构建一棵二叉树
，我这里就不找那道题了。
主要用前序遍历来构建树。
题目中所给的前序遍历，是用来定根的。遍历前序数组，遍历一个为一个根节点。
定完了树的根之后，从中序遍历的数组中找到根的值，并记录下标i，然后将数组中i的左边分为左树节点区间，将数组中i的右边分为右树节点区间。
创建根节点，然后再递归到左右区间中创建树即可。
这里就不画图了，就跟各位平时学校书里面让你们写这种题的做法一样，相信各位也是会画图的。
用一个子函数来创建树，方便记录二者的下标：
上面preorder的下标prei要用引用，和上面的那道题一样，preorder是挨个走的，每次都是只有一个，如果有想不通的同学，可以自己搞个例子画画图，就明白了。
代码
class Solution {
public:
TreeNode* creatTree(vector<int>& preorder, vector<int>& inorder, int& prei, int left, int right)
{
if(left > right)
return nullptr;
TreeNode* root = new TreeNode(preorder[prei++]);
int ini = 0;
for(ini = left; ini <= right; ++ini)
if(inorder[ini] == root->val) break;
root->left = creatTree(preorder, inorder, prei, left, ini - 1);
root->right = creatTree(preorder, inorder, prei, ini + 1, right);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int i = 0;
return creatTree(preorder, inorder, i, 0, inorder.size() - 1);
}
};
7. 从中序与后序遍历序列构造二叉树（力扣106）
题目描述
这道题和上面的那道不一样的就是把前序换成了中序。
解析
一样，通过后续来确定根节点。倒着走就行。
不过注意要先构建右子树再构建左子树。
代码
class Solution {
public:
TreeNode* _buildTree(vector<int>& inorder, vector<int>& postorder, int& posti, int inleft, int inright)
{
if(inleft > inright)
return nullptr;
TreeNode* root = new TreeNode(postorder[posti--]);
int ini = 0;
for(ini = inleft; ini <= inright; ++ini)
if(inorder[ini] == root->val) break;
root->right = _buildTree(inorder, postorder, posti, ini + 1, inright);
root->left = _buildTree(inorder, postorder, posti, inleft, ini - 1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder)
{
int i = postorder.size() - 1;
return _buildTree(inorder, postorder, i, 0, inorder.size() - 1);
}
};
8. 非递归实现二叉树的前序遍历（力扣144）
题目描述
很简单，就是前序遍历，但是不用递归的方法，题目最后也说了迭代，我们这里就用非递归来实现前序遍历。
不要觉得没什么用，有的厂面试的时候会考。
解析
怎么做呢，用栈。
前序遍历顺序为：根左右。
先访问再左右，如果我们画出图的话，可以找一个规律。
就是一个节点访问完后，访问其所有的左路节点，什么叫左路节点呢？
看图：
然后6没有右子节点，但是5有。
同理：
我们可总结如下：
遍历到一个节点时
- 先访问该节点
- 访问其左路节点
- 访问左路节点的右子树
右子树重复上述过程。
用栈的图解：
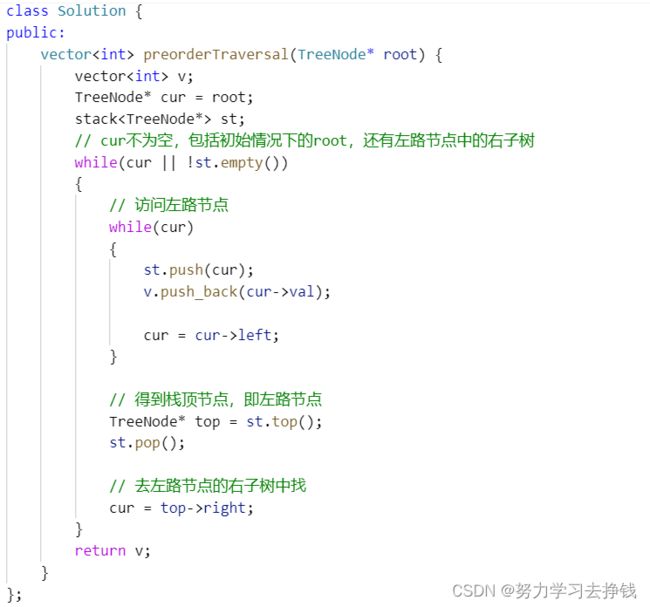
代码实现：
代码
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> v;
TreeNode* cur = root;
stack<TreeNode*> st;
// cur不为空，包括初始情况下的root，还有左路节点中的右子树
while(cur || !st.empty())
{
// 访问左路节点
while(cur)
{
st.push(cur);
v.push_back(cur->val);
cur = cur->left;
}
// 得到栈顶节点，即左路节点
TreeNode* top = st.top();
st.pop();
// 去左路节点的右子树中找
cur = top->right;
}
return v;
}
};
9. 非递归实现二叉树的中序遍历（力扣94）
题目描述
这道题和前一道代码一样，就是有的地方顺序调换了一下，各位还没解析的试着用上面那道题的思路来写写这道题。
解析
上面的那倒是前序遍历，后面的这道题是中序遍历，左根右。
思路一样，也是栈，不过是访问的时机变了一下。变成了从栈中弹出的时候再访问，因为当左路节点从栈中弹出的时候说明这个节点的左路节点已经访问过了，接下来就是访问根了。
就不画图了，好麻烦，直接给代码了：
代码
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> v;
TreeNode* cur = root;
while(cur || !st.empty())
{
while(cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
st.pop();
// 访问时机发生改变，其余都不变
v.push_back(top->val);
cur = top->right;
}
return v;
}
};
10. 非递归实现二叉树的后序遍历（力扣145）
题目描述
这里是非递归后序遍历。
跟上面两道稍微有点出入，有的地方绕一点。
解析
还是栈，但是细节要比前两道多一点点。
首先，后序遍历，左右根。
还是访问的时机要变一下，最后的时候再访问。
前序的可以直接访问，中序的栈弹出的时候再访问，后序怎么办？
左右都访问过了再访问，更准确点是右访问过了再访问。那么怎么记录这一点呢？
当左路节点从栈中弹出的时候说明这个节点的左路节点已经访问过了，接下来就是访问右了。
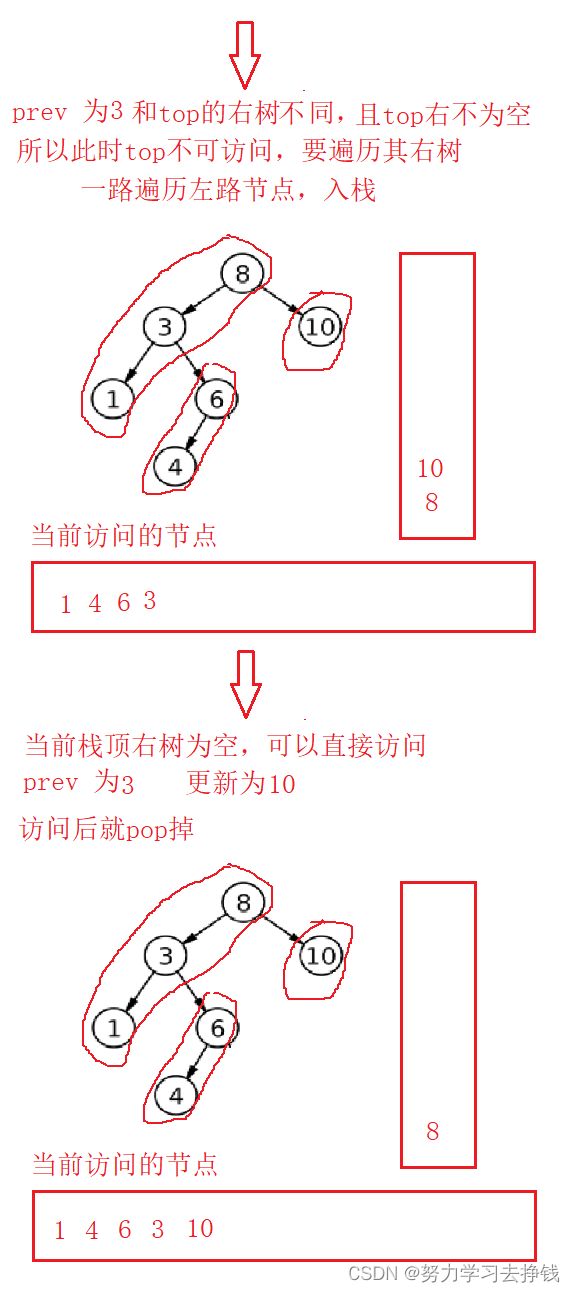
我们可以搞一个prev用来表示前一个访问到的节点，左右根，当要访问根的时候，前一个访问过的节点就是右。
我们可以访问根时分两种情况，一种是根的右为空，一种是根的右是prev。当访问到了当前节点后就将prev更新为当前访问到的节点。
来个图解：
然后给代码：
代码
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
stack<TreeNode*> st;
vector<int> v;
TreeNode* cur = root;
// prev节点，用来记录前一次访问的节点
TreeNode* prev = nullptr;
while(cur || !st.empty())
{
// 左路节点入栈
while(cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
// 当前节点右树为空和右树等于prev可以访问
if(prev == top->right || top->right == nullptr)
{
v.push_back(top->val);
prev = top;
cur = nullptr;
st.pop();
}
else // 否则就访问当前节点的右树
{
cur = top->right;
}
}
return v;
}
};
这十道题对于没有做过的同学来说，还是有点强度的，做过的同学可能也有点。
反正都是经典好题，各位好好琢磨琢磨。
到此结束。。。