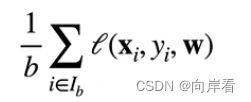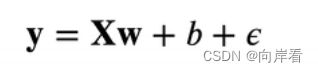动手学深度学习（二）线性神经网络
推荐课程：跟李沐学AI的个人空间-跟李沐学AI个人主页-哔哩哔哩视频
回归任务是指对连续变量进行预测的任务。
一、线性回归
线性回归模型是一种常用的统计学习方法，用于分析自变量与因变量之间的关系。它通过建立一个关于自变量和因变量的线性方程，来对未知数据进行预测。
1.1 线性模型
举个例子，房价预测模型：
- 假设1︰影响房价的关键因素是卧室个数，卫生间个数和居住面积，记为x1，x2，x3。
- 假设2：成交价是关键因素的加权和，
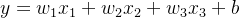
权重
和偏差
的实际值在后面决定。
- 给定n维输入，
![x=[x_1,x_2, ....x_n]^T](http://img.e-com-net.com/image/info8/6b5fddd7670d4227b58df1f04af14923.png)
，向量x对应于单个数据样本的特征。 - 线性模型有一个n维权重和一个标量偏差，
![w =[w_1, w_2, ..., w_n]^T](http://img.e-com-net.com/image/info8/21ca7ff1a97e4f18a1c4c271bdae1ad6.png)
，。权重决定了每个特征对预测值的影响。偏置是指当所有的特征都取0时，预测值应为多少。 - 输出是输入的加权和，
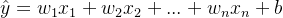。我们常用
表示预测值。
则，该房价预测模型为：
，这是一个线性预测模型。给定一个数据集（如x），我们的目标就是寻找模型的权重和偏置，使得根据模型做出的预测大体符合数据中真实价格
。也是就说最佳的权重和偏置有能力使得预测值逼近真实值，找到最佳的权重和偏置这是我们的最终目的。
1.2 损失函数（衡量预估质量）
用于比较真实值和预估值的差异，即以特定规则计算真实值和预估值的差值，例如房屋售价和估价。
假设是真实值，是预测值，平方差损失为 
，我们以该函数作为损失函数。
设训练集有n个样本，则这n个样本的损失均值为
Q：那么损失函数，对我们找到最优的权重
我们可以看到，最佳的预测值与真实值之间的损失值一定是尽可能小的，因此我们只要求得最小的损失值，那么得到这个损失值的权重
Q：怎么求得最小的损失值呢？
如，平方差损失函数是一个凹函数，那么求解最小的损失值，我们只需要将该函数关于
二、基础优化算法（梯度下降算法）
在绝大多数的情况下，损失函数是很复杂的（比如逻辑回归），根本无法得到参数估计值的表达式，也就无从获取没有显示解（解析解）。
此需要一种对大多数函数都适用的方法，这就引出了“梯度下降算法”，这种方法几乎可以优化所有深度学习模型。它通过不断地在损失函数递减的方向上更新参数来降低误差（原理）。
2.1 梯度下降公式
首先，我们需要确定初始化模型的参数
，接下来重复迭代更新参数t=1、2、3、....、n，更新权重的公式为：
其中，
为上一次更新权重的结果，
为学习率（这是一个超参数，决定了每次参数更新的步长），
为损失函数递增的方向（注意公式中为负）。
2.2 选择学习率
梯度下降的过程宛如一个人在走下山路，一步一步地接近谷底，学习率相当于这个人的步长。
学习率的选取不易过大，也不宜过小。学习率选取过大会使得权重更新的过程一直在震荡，而不是真正的在下降。学习率选取过小，会使得权重更新的过程十分缓慢，影响效率。
2.3 小批量随机梯度下降
一个神经网络模型的训练可能需要几分钟至数个小时，我们可以采用小批量随机梯度下降的方式来加快这一过程。
在整个训练集上计算梯度太昂贵了，因此可以随机采用 个样本
来求取整个训练集的近似损失（原理）。求近似损失公式为：
其中， 是批量大小，另一个重要的超参数。
Q：如何选择批量大小？
选择批量大小不能太小，也不能太大。批量大小选择过小，则每次计算量太小，不适合并行来最大利用计算资源。批量大小选择过大，内存消耗增加浪费计算，例如如果所有样本都是相同的。
三、线性回归的从零开始实现（代码实现）
3.1 生成数据集
首先，我们根据带有噪声的线性模型构造一个人造数据集，我们的目的是通过这个数据集来还原线性模型中正确的参数。
我们使用线性模型参数 ![\textup{w}=[2,-3.4]^T](http://img.e-com-net.com/image/info8/a6336d9fe4ca4607bf8c2520c12d50c2.png){kind=small}
，
和噪声项 
生成数据集及其标签。
# 生成数据集
def synthetic_data(w, b, num_examples):
"""生成 y=Xw + b + 噪声"""
X = torch.normal(0, 1, (num_examples, len(w))) # 正态分布（均值为0，标准差为1）
y = torch.matmul(X, w) + b # 矩阵相乘
y += torch.normal(0, 0.01, y.shape) # 加入噪声项
# 得到的y为行向量的形式，为了使其变为一列的形式需要进行reshape
return X, y.reshape((-1, 1))3.2 传输数据集
def data_iter(batch_size, features, labels):
num_examples = len(features)
indices = list(range(num_examples))
# 这些样本是随机读出的，没有特定的顺序
random.shuffle(indices)
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(indices[i:min(i+batch_size,num_examples)])
yield features[batch_indices],labels[batch_indices]