栈和队列的详解

目录

1. 栈的基本概念

1.1 栈的定义

1.2 栈的存储结构

1.3 栈的数学性质

2. 栈的基本操作

2.1 顺序栈定义

2.2  链式栈结点定义

3 栈输入输出的合理性

4 栈的全部输出结果

 5 栈的相关应用

5.1 括号匹配

5.2 进制转化

6  队列的基本概念

6.1 队列的定义

6.2  队列的存储结构

6.3  循环队列

7 队列的基本操作

7.1 顺序存储队列的基本操作

7.2  链式存储队列的基本操作

 8 队列的相关应用

8.1 杨辉三角（队列形式输出）

 9 总结

---

1. 栈的基本概念

1.1 栈的定义

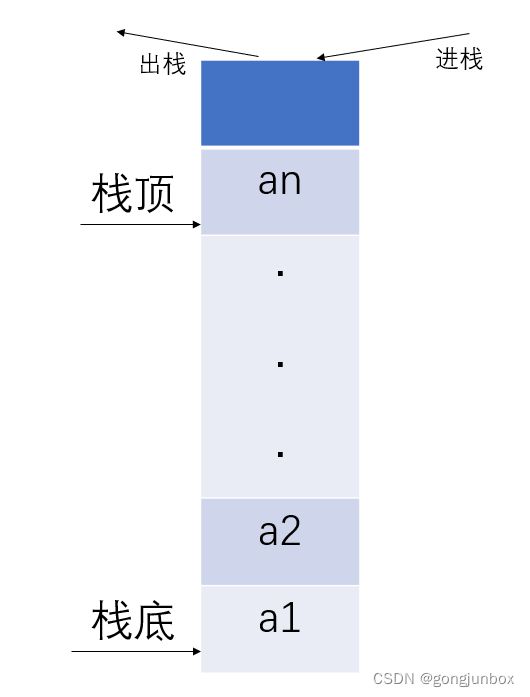
        栈(stack) 是限定仅在一端（表尾）进行插入或删除操作的线性表。因此，对栈来说，表尾端有其特殊含义，称为栈顶 (top), 相应地，表头端称为栈底 (bottom) 。不含元素的空表称为空栈。栈的示意图，如下图所示。

        栈的通俗解释：在从上往下堆积木时候，只能从最顶部放置积木，或者从最顶部拿走基本。积木最顶端叫做栈顶，积木最底端叫做栈底。从下往上堆积木的过程叫做堆栈或者压栈，从上往下拿走积木的过程叫做出栈。

1.2 栈的存储结构

        可用顺序表和链表来存储栈，栈可以依照存储结构分为两种；顺序栈和链式栈。在栈的定义中已经说明，栈是一种在操作上稍加限制的线性表，即栈本质上是线性表，而线性表有两种主要的存储结构—— 顺序表和链表，因此栈也同样有对应的两种存储结构。

1.3 栈的数学性质

        当n个元素以某种顺序进栈，并且可在任意时刻出栈（在满足先进后出的前提下）时，所获得的元 素排列的数目N恰好满足函数 Catalan（）的计算，最终有种排列方法。该公式称为卡特兰数。

2. 栈的基本操作

2.1 顺序栈定义

typedef struct{
    int data[maxSize];    //存放栈中元素，maxSize是已定义的常量
    int top;               //栈顶指针
}SqStack;                //顺序栈类型定义

（1） 构造一个空栈：InitStack(&S)

void InitStack(SqStack &S){
    s.top=-1;
}

（2）判断栈空：StackEmpty(SqStack S)

bool StackEmpty(SqStack S){
    if(S.top==-1)    //为空的是top指向-1
        return true;
    else
        return false;
}

（3）进栈： Push(SqStack &S,int x)

bool Push(SqStack &S,int x){
    if(S.top==MaxSize-1)       //判断是否栈满，满了推出
        return false;
    S.data[++S.top]=x;        //先将指针加一再入栈
    return true;
}

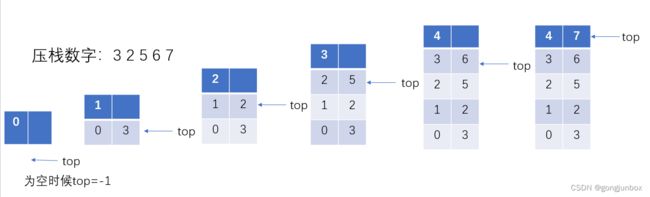
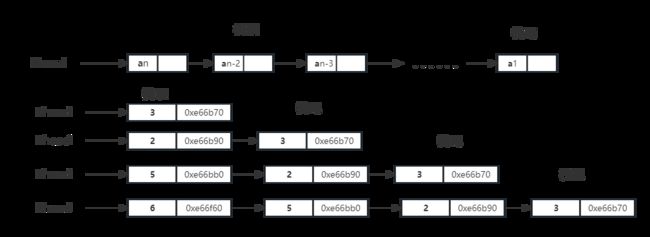
 以下是模拟压栈的整个过，以数字3 2 5 6 7为例进行压栈。第一行是栈元素在顺序表中的序号，第二行是栈数据。

 输入元素，左边为顺序表序号，右边是栈数据。

 注意：当栈为空时候，top=-1；每次插入时候，要先判断栈是否已满，就是top是否等于MaxSize-1，如果相等，就不能进行压栈。

（4）出栈：Pop(SqStack &S,int &x)

bool Pop(SqStack &S,int &x){
    if(S.top==-1)            //判断是否为空
        return false;    
    x=S.data[S.top--];        //先出栈，再指针减一
    return true;
}

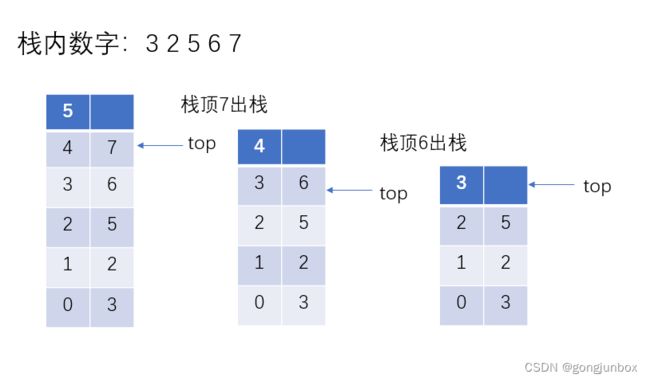
  以下是模拟出栈的整个过，以上述压栈后栈为例进行出栈。第一行是栈元素在顺序表中的序号，第二行是栈数据。

   输出栈顶元素，左边为顺序表序号，右边是栈数据。

  注意：每次出栈时候，要先判断栈是否为空，就是top是否等于-1，如果相等，就不能进行出栈。

（5） 读栈顶元素：GetTop(SqStack S,int &x)

bool GetTop(SqStack S,int &x){
    if(S.top==-1)        //判断是否为空
        return false;
    x=S.data[S.top];
    return true;
}

2.2  链式栈结点定义

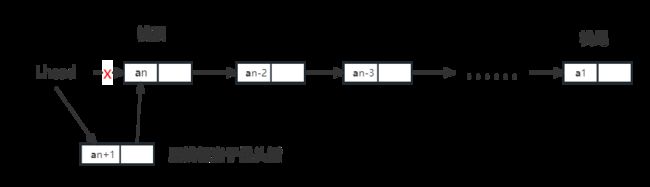
链式栈的优点：便于多个栈共享存储空间和提高其效率，不存在找满上溢的情况。通常采用单链长实现，并规定所有操作都是在单链表的表头进行的。这里规定链栈没有头结点、 Lhead指向找顶元素，所以在压栈时候采用头插法进行压栈建立链表。

链式栈的存储结构

typedef struct LNode{
    int  data;        //数据域
    struct LNode *next;    //指针域
}LNode;                //链式栈结点定义

（1） 构建一个空栈

void InitStack(LNode *&LStack){
    LStack=(LNode*)malloc(sizeof(LNode)); //制造一个头结点
    LStack->next=NULL;
}

注意：判断栈是否为空，也是根据初始栈的LStack->next=NULL来判断

 （2）判断栈是否为空

bool IsEmpty(LNode *LStack){
    if(LStack->next==NULL)
        return true;
    return false;
}

（3）进栈

void push(LNode *LStack,int x){
    LNode *p;
    p=(LNode*)malloc(sizeof(LNode));
    p->next=NULL;

    //头插法
    p->data=x;
    p->next=LStack->next;
    LStack->next=p;
}

注意：在插入时候，无需和顺序栈一样要判断是否栈满，因为链式栈是链表，只要条件运行，链表就不会存在满的状态。

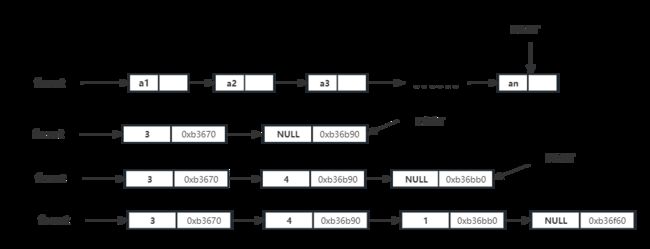
以下是头插法插入栈顶元素。 

 以下是模拟插入链式栈的运行情况如图。以数字3 2 5 6为例进行压栈。

 以下是该是平台直观显示出来的栈位置，结点左边为数据，右边为该结点地址，靠经Lhead的结点为栈顶，尾部为栈尾。

（4）出栈

bool Pop(LNode *LStack,int &x){
    LNode *p;
    if(LStack->next==NULL)
        return false;
    //相当于单链表的删除操作
    p=LStack->next;
    x=p->data;
    LStack->next=p->next;
    free(p);
    return true;
}
    

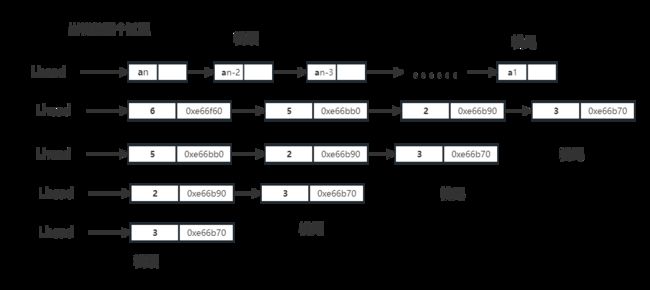
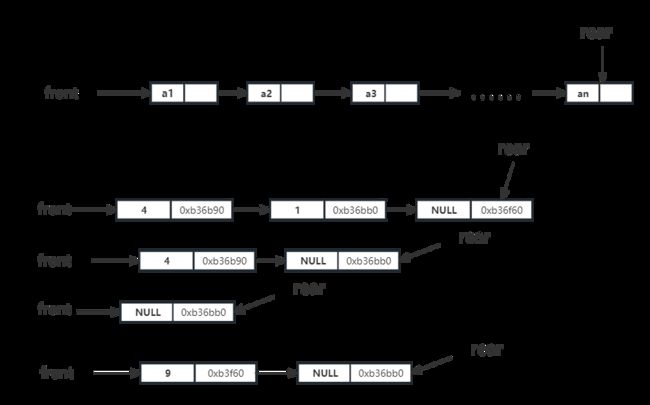
 以下是模拟链式栈出栈的运行情况如图。以上述数字3 2 5 6，进栈后，再出栈为例。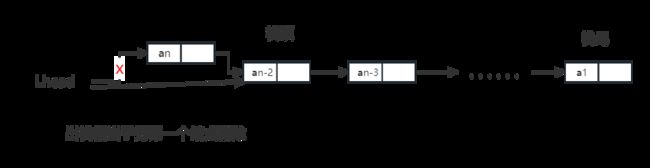

  以下是该是平台直观显示出来的栈位置，结点左边为数据，右边为该结点地址，靠经Lhead的结点为栈顶，尾部为栈尾。

注意：在链式栈中出栈，还是先要判断是否栈为空，如果为空就不能进行出栈。

说明∶对于链栈，和顺序栈一样，只是它们的存储方式不同，但是相关基本操作都说类似的，只需记住，栈如何判空，是否栈满，以及进栈和出栈只能从栈顶操作。

3 栈输入输出的合理性

        栈的输入输出合理主要在于栈的特性，而栈的特性主要是先进后出，每次在栈顶进行出栈和压栈的相关操作，无论怎样输入，每次输出顺序都是和输出相反的顺序。一旦输出的顺序与输入顺序不是完全逆序的，则可以判定该栈的输入输出是不合理的。

       （1） 以输入3 2 6 5 8一串元素，出栈顺序8 5 6 2 3 为例，进行判断栈的合法性。

         接下来是模拟入栈和出栈操作

         从模拟结果可以看出，该入栈顺序和出栈顺序是合法的。

        （2）以输入3 2 6 5 8一串元素为例，出栈顺序8 2 3 5 6 为例，进行判断栈的合法性。

         接下来是模拟入栈和出栈操作

        在出栈时候，可以发现在弹出元素8之后，本应该弹出元素5，但是设定的元素8后面输出2，所以在此可以发现，出栈序列不合法。

4 栈的全部输出结果

（1）栈大小无限制输出结果     

        以4个元素的栈为例，输出全部栈的出栈结果。（在压栈和出栈时候，可以随时选择出栈、压栈，但是都在栈顶操作，不过栈为空时候，就不能进行出栈）

        四个元素进行出栈入栈，总共要产生总合法出栈的方法。但是如果不按照出栈入栈的合法顺序来进行，应该存在种情况产生。所以栈的输入输出方式，很大程度限制了出栈入栈的合法个数。

（2）栈大小有限制输出结果

        在限制栈的大小时候，又将减少合法出栈序列。因为栈里最多存在三个元素，所以必然要等有些元素出栈后，排在后面的元素才能进行入栈。下列将上述栈的大小改为3，所以就减少了四个元素同时在栈中的情况，合法出栈序列从14种减少为13种。

 5 栈的相关应用

5.1 括号匹配

算法思想：在遍历存放字符数组中，如果遇到（、{、[ 等左括号，就将其压入栈中，在遇到 ）、}、] 等右括号之后，就需要从栈中出栈判断是否有对应的左括号与之匹配，如果存在，则将其出栈，后继续遍历字符数组。

#include 
#include 

#define MAXSIZE 100
typedef int datatype;
typedef struct sequence_stack
{
    datatype a[MAXSIZE];
    int top;
} seq_stack;

void init(seq_stack* st)        //初始化栈，生成一个初始栈
{
    st->top = 0;
}
    
int empty(seq_stack st)           //判断栈是否为空
{
    return( st.top ? 0:1 );
}

datatype top(seq_stack st)        //取栈顶元素
{
    if (empty(st))
    {
        printf("\n栈是空的!");
        exit(1);
    }

    return st.a[st.top-1];
}

void push(seq_stack* st, datatype x)    //进行压栈
{
    if(st->top == MAXSIZE)            //判断栈是否已经满了
    {
        printf("\nThe sequence stack is full!");
        exit(1);
    }

    st->a[st->top]=x;
    st->top++;
}

void pop(seq_stack* st)        //进行出栈
{
    if(st->top==0)            //判断栈是否为空
    {
        printf("\nThe sequence stack is empty!");
        exit(1);
    }

    st->top--;
}

int match_kuohao(char c[])        //括号匹配算法
{
    int i=0;
    sequence_stack s;            //新建一个栈
    init(&s);
    while(c[i]!='#')            //进行输入括号
    {
            switch(c[i])
            {
            case '{':
            case '[':
            case '(':     push(&s,c[i]); break;                // 开括号全部入栈
            case '}':     if( !empty(s) && top(s)=='{'  )   // 假如 {和}匹配
                          {pop(&s); break;}
                          else return 0;
            case ']':     if( !empty(s) && top(s) == '[' )      // 假如 [和]匹配
                          {pop(&s); break;}
                          else return 0;
            case ')':     if( !empty(s)&& top(s)=='('  )      // 假如 (和)匹配
                          {pop(&s); break;}
                          else return 0;
            }

            i++;
    }

    return (empty(s));        //栈为空则匹配,否则不匹配
}


int main()
{
    char szKuohao[] = "(([(){}]))#";

    int result = match_kuohao(szKuohao);
    if(result == 1)
        printf("匹配成功！\n");
    else
        printf("匹配不成功！\n");

    return 0;
}

5.2 进制转化

算法思想：十进制数 和其他 进制数的转换是计算机实现计算的基本问题，其解决方法很 多，其中一个简单算法基千下列原理：

         N=(N div d)Xd+N mod d (其中： div 为整除运算， mod 为求余运算）

        假设现要编制一个满足下列要求的程序：对于输入的任意一个非负十进制整数，打印 输出与其等值的八进制数。由千上述计算过程是从低位到高位顺序产生八进制数的各个数位，而打印输出，一般来说应从高位到低位进行，恰好和计算过程相反。因此，若将计算 过程中得到的八进制数的各位顺序进栈，则按出栈序列打印输出的即为与输人对应的八进制数。

#include
void change(int m, int n)
{
	int a[100];
	int top=0;
	while(m)
	{
		a[top++]=m%n;
		m=m/n;
	}
		top--;
		while(top>=0)
		{
			if(a[top]>9)
				printf("%c",a[top]+'A'-10);
			else printf("%c",a[top]+'0');
			top--;
		}
}
int main()
{
	int m,n;
	printf("输入要转换的十进制数：");
		scanf("%d",&m);
	printf("要转换的进制：");
		scanf("%d",&n);
	change(m,n);
	printf("\n");
	return 0;
｝

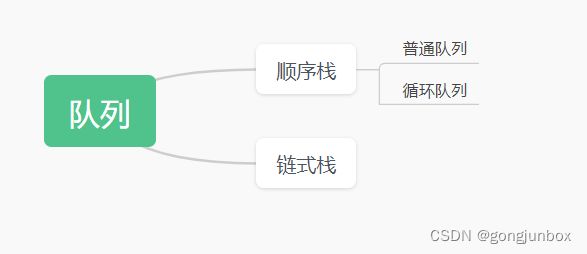
6  队列的基本概念

6.1 队列的定义

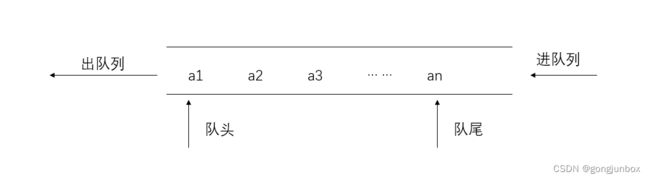
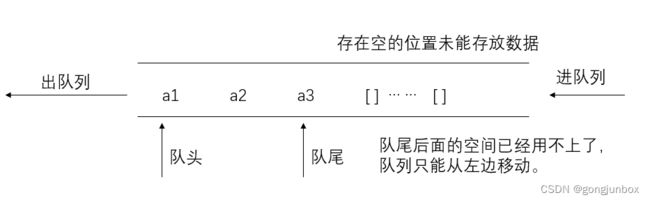
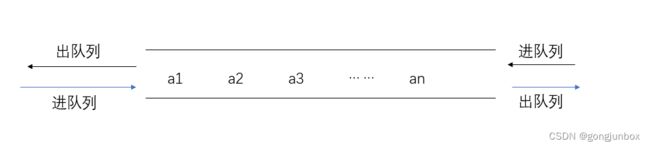
        队列(queue)是一种先进先出( first in first out,缩写为FIFO)的线性表。它只允许在表的一端进行插入，而在另一端删除元素。这和我们日常生活中的排队是一致的，最早进入队列的元素最早离开。在队列中，允许插入的一端叫做队尾 (rear), 允许删除的一端则称为队头 (front) 。假设队列 q= (a1 ,a2, …， an)，那么，a1 就是队头元素， an 则是队尾元素。队列中的元素是按照 a1 ,a2, …， an 的顺序进入的，退出队列也只能按照这个次序依次退出，也就是按照a1 ,a2, …， an顺序，只有当前面的都离开队列后，an+1才能离开队列。

        通俗的解释：在人们排队买东西时候，都是先到收银台的顾客先出超市，只有等排在前面的顾客结完账之后，后面的顾客才能结账。也就是所谓的先进先出。

6.2  队列的存储结构

        可用顺序队和链队来存储队列，队列可以依照存储结构分为两种；顺序栈和链式栈。在队列的定义中已经说明，队列是一种在操作上稍加限制的线性表，即栈本质上是线性表，而线性表有两种主要的存储结构—— 顺序表和链表，因此队列也同样有对应的两种存储结构。顺序队又有普通队列和循环队列，是根据队列的特定从普通队列转化形成的循环队列，用于节省存储空间。

        由于普通队列在运行时候，最终会将队头和队尾指向同一个元素，导致虚假的队列满的状态，可是队列中却还有很多在队头和队尾没有包括的地方为空，从而产生空间的浪费。

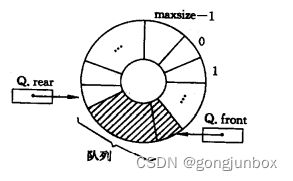
6.3  循环队列

        循环链表就是将一个顺序队列变成一个环状队列，使其前后可以相连，但是这种环状是人为想象出来的，在计算机实际存储过过程中，还是顺序结构。这种环是一种逻辑结构，方便存储。

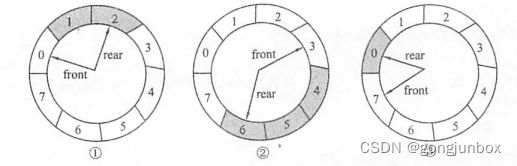
① 由空队进队两个元素，此时 front指向0，rear 指向2。

②进队4个元素，出队3个元素，此时 front 指向3，rear指向6。

③进队2个元素，出队4个元素，此时 front指向7，rear指向0。

        由①到③的变化过程可以看出，经过元素的进进出出，即便是 rear和 front都到了数组尾端，依然可以让元素继续入队，因为两指针不是沿着数组下标递增地直线行走，而是沿着一个环行走，走到数组尽头时自动返回数组的起始位置。

队列满条件：（rear+1）%Maxsize==front

队列为空条件：rear=front

队列中元素个数：（rear-front+Maxsize）%Maxsize

7 队列的基本操作

7.1 顺序存储队列的基本操作

#define Maxsize 50
typedef struct{
    int data[Maxsize];
    int front,rear;
}SqQueue;

（1）构建一个空的队列

void InitQueue(SqQueue &Q){
    Q.rear=Q.front=0;
}

（2）判断队列是否为空

bool IsEmpty(SqQueue Q){
    if(Q.rear==Q.front)
        return true;
    return false;
}

（3）入队

bool EnQueue(SqQueue &Q,int x){
    if((Q.rear+1)%Maxsize==Q.front)    //判断队列是否满了
        return false;
    Q.data[Q.rear]=x;
    Q.rear=(Q.rear+1)%Maxsize;
    return true;
}

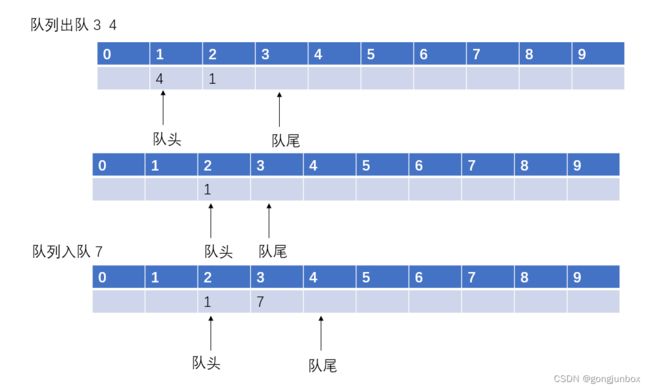
        以下是模拟入队的整个过，以元素 3 4 1为例进行入队操作，整个顺序队列的Maxsize=10。第一行是队内元素在顺序表中的序号，第二行是队列元素数据。 

        以下是该是平台直观显示出来的队列位置，上方为队列位置，下方为该元素值。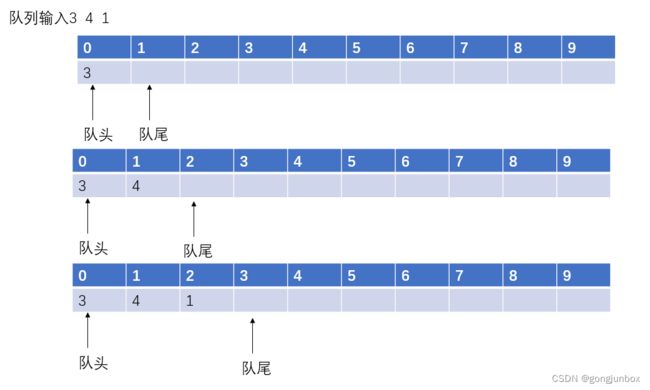

注意：在入队之前，都需要判断队列是否已满，如果已满，则不然进行入队。

（4）出队

bool DeQueue(SqQueue &Q,int &x){
    if(IsEmpty(Q))    //判断队列是否为空
        return false;
    x=Q.data[Q.front];
    Q.front=(Q.front+1)%Maxsize;
    return true;
}

        以下是模拟出队的整个过，以上述入队之后情况为例进行出队3 4 元素和入队7元素操作，整个顺序队列的Maxsize=10。第一行是队内元素在顺序表中的序号，第二行是队列元素数据。 

         以下是该是平台直观显示出来的队列位置，上方为队列位置，下方为该元素值。

 注意：在出队之前，都需要判断队列是否为空，如果为空，则不然进行出队操作。

7.2  链式存储队列的基本操作

typedef struct LinkNode{    //链式队列结点
    int data;
    struct LinkNode *next;
}LinkNode;
typedef struct{            //链式队列
    LinkNode *front,*rear;    //队列的队头和队尾指针
}LinkQueue;

（1）构建一个队列

void InitQueue(LinkQueue &Q){
    Q.front==Q.rear=(LinkNode*)malloc(sizeof(LinkNode));
    if(!Q.front)     //存储分配失败
        exit(OVERFLOW);    
    Q.front->next=NULL;
}

（2）判断队是否为空

bool IsEmpty(LinkQueue Q){
    if(Q.front==Q.rear)
        return true;
    return false;
}

（3）入队

类似于尾接法，把每次进入的插入到rear后面。

void EnQueue(LinkQueue &Q,int x){
    LinkNode *p= (LinkNode *)malloc(sizeof(LinkNode));
    p->data=x;
    p->next=NULL;
    Q.rear->next=s;
    Q.rear=s;
}

  以下是模拟队列入队的运行情况如图。以数字3  4  1为例进行入队。

   以下是该是平台直观显示出来的队列位置，结点左边为数据，右边为该结点地址，靠近左边的结点为队首front，尾部为队尾rear。

 注意：在链队里面，和链式栈一样，都是不用考虑空间大小的。

（4）出队

类似于删除链表的第一个结点。

bool DeQueue(LinkQueue &Q,int &x){
    if(Q.front==Q.rear)        //判断是否为空
        return false;
    LinkNode *p=Q.front->next;
    x=p->data;
    Q.front->next=p->next;
    if(Q.rear==p)                //如果队列原来只有一个结点，删除后变成空队列
        Q.rear=Q.front;
    free(Q);
    reurn true;
}

  以下是模拟队列出队的运行情况如图。以上诉3  4  1入队后为例进行出队，再进行一次入队操作，将元素 7 入队。 

    以下是该是平台直观显示出来的队列位置，结点左边为数据，右边为该结点地址，靠近左边的结点为队首front，尾部为队尾rear。

  注意：在链队里面，和链式栈一样，都是需要考虑是否为空的，如果为空，则不能进行出队。

 8 队列的相关应用

8.1 杨辉三角（队列形式输出）

（1）左上的元素，出队列为temp=1，并且打印temp=1, 取出队后现在队首为x=3

（2）求下一行元素temp=temp+x

（3）到最后1前面那个数字也就是3停止遍历

（4）循环外面出队列打印最后一个一个元素 1 ，并且存储下一行最后一个元素数字 1

下面是打印第四行，将第五行存入队列的全过程。

#include
#define Maxsize 50
typedef struct{
    int data[Maxsize];
    int front,rear;
}SqQueue;

void InitQueue(SqQueue &Q){
    Q.rear=Q.front=0;
}

bool IsEmpty(SqQueue Q){
    if(Q.rear==Q.front)
        return true;
    return false;
}

bool EnQueue(SqQueue &Q,int x){
    if((Q.rear+1)%Maxsize==Q.front)    //判断队列是否满了
        return false;
    Q.data[Q.rear]=x;
    Q.rear=(Q.rear+1)%Maxsize;
    return true;
}

bool DeQueue(SqQueue &Q,int &x){
    if(IsEmpty(Q))    //判断队列是否为空
        return false;
    x=Q.data[Q.front];
    Q.front=(Q.front+1)%Maxsize;
    return true;
}

bool GetTop(SqQueue Q,int &x){
	if(IsEmpty(Q))
		return false;
	x=Q.data[Q.front];
	return true;
} 

void YangHuiTriangle(int N){
	int n,x,i,temp;
	SqQueue Q;
	InitQueue(Q); 
	
	EnQueue(Q,1);
	for(n=2;n<=N;n++){		//每一行进行打印 
		EnQueue(Q,1);		 //每行第一个都是数字 1	
		for(i=1;i<=n-2;i++){	//通过上一行求下一行 （第一行已知，所以可以求出第二行，依次类推）
			DeQueue(Q,temp);	//先取出最前面的元素，也就是要求下一行的左上方的元素 
			printf("%d ",temp);	//将其打印 
			GetTop(Q,x);	//得到上述出队后，当前最前方元素，也就是要求下一行的上方的元素 
			temp=temp+x;	//得到当前要求元素 
			EnQueue(Q,temp);	//将其入队 
		}
		DeQueue(Q,x);	//输出上一行最后一个 1	
		printf("%d ",x);
		EnQueue(Q,1);		//存储要求这一行最后一个数字 1 
		printf("\n");	//输出上一行的换行 
	}
	while(!IsEmpty(Q)){	//输出最后一行 
		DeQueue(Q,x);
		printf("%d ",x);
	}

}

int main(){
YangHuiTriangle(7);
	return 0;
}

 9 总结

        栈和队列的区别：栈是先进后出， 队列是先进先出，主要还是在逻辑层面，我们认为设定了顺序表或者链表的进出顺序，然后利用这些特性进行专门领域的运用。

        读者也就根据栈和队列的特性，自己总结出相关先进先出，或者先进后出等一系列生活中能运用到的，比如汉诺塔运用栈的先进后出可以解决问题；迷宫不仅可以运用栈的先进后出，也可以运用队列的先进先出进行回溯找寻出口位置。

        我们知道双端队列是两端都能进出，可以自己限制进出方式，使其拥有一定的特性。比如限制左边不能进，右边不能出。

        在双端队列进队时，前端进的元素排列在队列中后端进的元素的前面，后端进的元素排列在队列中前端进的元素的后面。在双端队列出队时，无论是前端还是后端出队，先出的元素排列在后出的元素的前面。思考：如何由入队序列a，b，c，d得到出队序列c，d，a， b?

        那限制右端不能进之后呢，如何由入队序列a，b，c，d得到出队序列c，d，a， b?  这些都说读者值得思考的问题。

参考资料：

[1] 苏小红，孙志刚，陈惠鹏等编著. C语言大学实用教程（第四版）[M]. 北京：电子工业出版社，2017.
[2] 严蔚敏，吴伟民. 数据结构[M]. 北京：清华大学出版社.

作者：

江西师范大学_姜嘉鑫；   江西师范大学_龚俊