python/gurobi计算二人零和博弈纳什均衡精确解(可求解大规划策略空间)

python/gurobi计算二人零和博弈纳什均衡精确解(可求解大规划策略空间)

​
二人零和博弈描述了涉及两名参与人的严格竞争情况(每一组动作对应的效用和为0)， 矩阵博弈是具有有限策略集的两人零和博弈（如下图）。

​ 矩阵博弈在很多方面都很有趣，并且由于其简单性和特殊结构，它们的分析很容易处理。 冯·诺依曼和摩根斯坦表明，线性规划可以用来解决这些博弈。 在二人零和博弈中有以下重要性质：

1. 二人零和博弈的纯策略纳什均衡（如果存在）恰恰是鞍点。
2. 两个参与人的最佳策略可以用彼此对偶的线性规划来描述。
3. 极小极大定理：在二人零和博弈中minmax=maxmin。
4. 极大极小定理表明每个矩阵博弈都保证有一个混合策略纳什均衡。通过求解两个互为对偶的线性规划问题可以求解其混合策略NE。

​ 下面分别介绍求解二人零和博弈的纯策略NE的方法及相关定义和定理，并在最后赋上了用python求解的代码。

1 二人零和博弈的纯策略NE——鞍点

定义1：最大最小值

​ 给定一个矩阵博弈A，其最大最小值定义为：
$$\underline{v}=\underset{i\in S_1}{\max }\underset{j\in S_2}{\min }{a}_{ij}$$
​ 最大最小值maxmin是当列玩家可以自由使用任何策略时，对行玩家的最小保证回报(因为当前考虑的以及是列玩家采取动作使行玩家获得奖赏最少的情况了，列玩家已经没办法使得行玩家获得比maxmin更少的回报)。行玩家获得回报maxmin的策略称为玩家的最大最小策略。

定义2：最小最大值

​ 给定一个矩阵博弈A，其最小最大值定义为：
$$\overline{v}=\underset{j\in S_2}{\min }\underset{i\in S_1}{\max }{a}_{ij}$$
​ 最小最大值minmax是当行玩家可以自由使用任何策略时，对列玩家的最小保证损失(因为当前考虑的以及是行玩家采取动作使列玩家损失最大的情况了，行玩家已经没办法使得列玩家获得比minmax更大的损失)。列玩家获得损失minmax的策略称为玩家的最小最大策略。

定义3：矩阵的鞍点

​ 给定一个矩阵博弈A，一个点为鞍点的充分必要条件为：该点在所在行中为最小值，在所在列中为最大值。

定理1

​ 一个矩阵A有一个鞍点当且仅当$\underline{v}=\overline{v}$。

命题1：纯策略NE的充要条件

​ 对于具有收益矩阵A的矩阵博弈，$a_{ij}$是鞍点当且仅当策略(i,j)为纯策略纳什均衡。

​ 综上可知，要求二人零和博弈的纯策略均衡，只需要找到收益矩阵的鞍点。但并不是每个二人零和博弈都有纯策略纳什均衡，接下来介绍混合策略纳什均衡。

2. 二人零和博弈的混合策略NE——对偶的线性规划

​ 我们已经看到矩阵游戏中可能不存在鞍点或纯策略纳什均衡。 然而，当允许混合策略时，均衡肯定存在。 令$x=\left(x_1,\dots ,x_m\right)$和$y=\left(y_1,\dots ,y_n\right)$分别为行玩家和列玩家的混合策略。 注意$a_{ij}$是当行玩家选择行$i$而列玩家选择列$j$的概率为1时行玩家的收益。列玩家对应的收益为$-a_{ij} $。 使用上述混合策略 $x$ 和 $y$ 的行玩家的预期收益可以计算为：
$$\begin{array}{rl}& =u_1(x,y)\\ & =\sum _{i=1}^m\sum _{j=1}^n{x}_i{y}_j{a}_{ij}\\ & =xAy\text{ where }x=\left(x_1,\dots ,x_m\right);y=\left(y_1,\dots ,y_n\right);A=\left[a_{ij}\right]\end{array}$$
​ 列玩家的预期收益为$-xAy$。使用前面分析纯策略时的方法可知：

1. 行玩家的安全策略

   当行玩家使用混合策略 $x$ 时，它可以保证预期的收益为：
   $$\underset{y\in \Delta \left(S_2\right)}{\min }xAy$$
   因此，行玩家应该寻找一种混合策略 $x$ 来最大化上述收齐。 也就是：
   $$\underset{x\in \Delta \left(S_1\right)}{\max }\underset{y\in \Delta \left(S_2\right)}{\min }xAy$$
   ​ 也就是说行玩家的最优策略是进行最大最小化，这种行玩家的策略也被称为行玩家的安全策略。

2. 列玩家的安全策略

​ 类似地，当列玩家玩 $y$ 时，她要确保自己的收益为：
$$\begin{array}{rl}& =\underset{x\in \Delta \left(S_1\right)}{\min }-xAy\\ & =-\underset{x\in \Delta \left(S_1\right)}{\max }xAy\end{array}$$
​ 也就是说，她保证自己的损失不会超过
$$\underset{x\in \Delta \left(S_1\right)}{\max }xAy$$
​ 列玩家的最优策略应该是最小化这种损失：
$$\underset{y\in \Delta \left(S_2\right)}{\min }\underset{x\in \Delta \left(S_1\right)}{\max }xAy$$
​ 这称为最小化最大化。 列玩家的这种策略也被恰当地称为列玩家的安全策略。

​ 将上面两个策略的形式改写，可以得到：

1. 行玩家的优化问题
   $$\begin{array}{rl}& \mathrm{maximize}\underset{j}{\min }\sum _{i=1}^m{a}_{ij}{x}_i\\ & \text{ subject to }\\ & \sum _{i=1}^m{x}_i=1\\ & x_i\ge 0i=1,\dots ,m\end{array}$$

2. 列玩家的优化问题

$$\begin{array}{rl}& \mathrm{minimize}\underset{i}{\max }\sum _{j=1}^n{a}_{ij}{y}_j\\ & \text{ subject to }\\ & \sum _{j=1}^n{y}_j=1\\ & y_j\ge 0j=1,\dots ,n\end{array}$$

​ 定理：最大最小值定理

对于每一个$A_{m\times n}$ 的矩阵博弈，都有一个行玩家的混合策略$x^{\ast }=\left(x_1^{\ast },\dots ,x_m^{\ast }\right)$ 和一个列玩家的混合策略 $y^{\ast }=\left(y_1^{\ast },\dots ,y_n^{\ast }\right)$ ,使得：
$$\underset{x\in \Delta \left(S_1\right)}{\max }xA{y}^{\ast }=\underset{y\in \Delta \left(S_2\right)}{\min }{x}^{\ast }Ay$$
​ 也即：
$$\underset{x\in \Delta \left(S_1\right)}{\max }\underset{y\in \Delta \left(S_2\right)}{\min }xAy=\underset{y\in \Delta \left(S_2\right)}{\min }\underset{x\in \Delta \left(S_1\right)}{\max }xAy$$
同时，$\left(x^{\ast },y^{\ast }\right)$ 是一个混合策略纳什均衡。

​ 通过将上述两个优化问题进行改写，可以得到一组对偶线性规划问题，用于求解二人零和博弈的混合策略纳什均衡:

（1）LP1
$$\begin{array}{rl}& \text{ maximize }z\\ & \text{ subject to }\\ & z-\sum _{i=1}^m{a}_{ij}{x}_i\le 0j=1,\dots ,n\\ & \sum _{i=1}^m{x}_i=1\\ & x_i\ge 0\forall i=1,\dots ,m\\ & \end{array}$$

（2）LP2
$$\begin{array}{rl}& \mathrm{minimize}w\\ & \text{ subject to }\\ & w-\sum _{j=1}^n{a}_{ij}{y}_j\ge 0i=1,\dots ,m\\ & \sum _{j=1}^n{y}_j=1\\ & y_j\ge 0\forall j=1,\dots ,n\end{array}$$
​ 基于上面的定理，只需要求解出上面两个互为对偶的规划问题LP1、LP2，并且保证求出的最优目标函数值相同，此时对应的解x和y,即为混合策略纳什均衡。

3.python+gurobi程序实现

1. 纯策略纳什均衡——鞍点

   Tag =False
   Mat=np.array(Mat)
   [m,n]=Mat.shape
   SP_List=[]#鞍点的集合
   for i in range(m):
       for j in range(n):
           if Mat[i,j]==min(Mat[i,:]) and Mat[i,j]==max(Mat[:,j]):
               SP_List.append((i,j))
               if len(SP_List):
                   Tag=True
                   r=choice(SP_List)
   

   2.借助python+gurobi求解混合策略均衡

model = Model('LP1')
# 变量
z = model.addVar(lb = -np.inf,vtype = GRB.CONTINUOUS, name = 'z') # 注意gurobi里默认变量大于等于0，对于可取负数的变量，要格外设定
x = model.addVars([i for i in range(m)],lb = 0,vtype = GRB.CONTINUOUS, name = 'x') #[0,1]之间的连续变量
model.update()
# 目标函数
model.setObjective(z, GRB.MAXIMIZE)
# 约束
model.addConstr(quicksum(x)==1, name = 'c1')
for j in range(n):
    model.addConstr((np.mat(z)-np.mat(Mat[:,j])@(x.select())).tolist()[0][0]<=0, name = 'c%d'%(j+2))
# 求解
model.setParam('outPutFlag', 0)  # 0表示不输出求解日志
model.setParam('DualReductions', 0)
model.optimize()
# 输出
print('LP1求解状态：', model.Status)  # 显示当前求解状态
model.write('lp1.lp')
if model.Status==3:
    print('LP1 is infeasible')
    p1 = None
else:
    print('obj1=', model.objVal)
    p1 = [(model.getVars()[i]).x for i in range(1, m + 1)]

# LP2
model = Model('LP2')
# 变量
w = model.addVar(lb=-np.inf,vtype = GRB.CONTINUOUS, name = 'w') # 注意gurobi里默认变量大于等于0，对于可取负数的变量，要格外设定
y = model.addVars([i for i in range(n)],lb = 0,vtype = GRB.CONTINUOUS, name = 'y') #[0,1]之间的连续变量
model.update()
# 目标函数
model.setObjective(w, GRB.MINIMIZE)
# 约束
model.addConstr(quicksum(y)==1, name = 'c1')
for i in range(m):
    model.addConstr((np.mat(w)-np.mat(Mat[i,:])@(y.select())).tolist()[0][0]>=0, name = 'c%d'%(i+2))
# 求解
model.setParam('outPutFlag', 0)  # 不输出求解日志
model.optimize()

# 输出
print('LP2求解状态：',model.Status) # 显示当前求解状态
model.write('lp2.lp')
if model.Status == 3:
    print('LP2 is infeasible')
    p2 = None
else:
    print('obj2=', model.objVal)
    p2 = [(model.getVars()[i]).x for i in range(1, m + 1)]

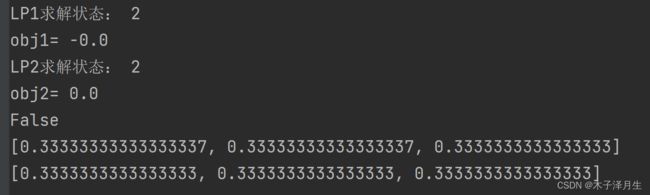
4.实现效果

针对剪刀石头布博弈，该算法的求解结果为：

其中，求解状态为2表示已经找到最优解，而两个优化问题的目标函数值相同，说明找到的就是混合策略纳什均衡，即以均匀概率随机出剪刀/石头/布。经测试，目前该算法可适用于大规模策略空间下的二人零和博弈。