学习报告 21-01-28
1、层次分析法AHP
2、单片机学习
层次分析法AHP
将半定性，半定量的问题转化为定量计算的一种行之有效的方法。
成对比较矩阵和正互反矩阵
设要比较n个因素C1,C2,……Cn对目标O的影响，从而确定他们在O中所占的比例，每次取两个因素Ci和Cj，用aij表示Ci与Cj对O的影响程度之比，按一到九的比例标度来衡量aij。N个元素彼此两两比较，全部结果可用如下的成对比较矩阵表示：
A=(aij)n*n,aij>0,aji=1/aij，aii=1 (I,j=1,2……n)
如果一个正互反矩阵满足aij*ajk=aik，则为一致性矩阵，简称一致阵。
从准则层到目标层（获得各因素的权重）
权向量和一致性指标
Cn的权数组为（w1，w2……wn）T ，Ci与Cj的相对权比重为aij=wi/wj，组成矩阵：
此即为一致阵。
N阶一致阵性质
A的秩为1，A的唯一特征根为n。A的任一列向量都是对应于特征根n的特征向量。因此在一致阵中，可以取对应于特征n的归一化特征向量表示诸因素的权重，这个向量称为权向量。如果A阵不一致，可采用A的最大特征根λmax对应的特征向量w(上加箭头)=(w1,w2……wn）t,作为权向量，即w满足
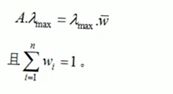在这种情况下，当λmax比n大得多，A的不一致性就越大，用特征向量作为权向量的误差就就会越大，因此可用λmax-n的大小来衡量A的不一致程度，定义一致性指标CI,CI=（λmax-n）/（n-1），由于Σni=1λ=n，实际上CI相当于n-1个特征根λ2……λn（最大特征根λmax除外）的平均值。
平均随机一致性指标RI
对固定的n，随机构造正互反矩阵A‘，其中a’ij是从1，2，……9……1/9中随机抽取，这样的A‘是最不一致的，取充分大的子样（如500个），得到A’最大特征值λ‘max.RI=（λ‘max-n）/（n-1）
Matlab计算平均一致性指标
n=1;
P=[1,2,3,4,5,6,7,8,9,1/2,1/3,1/4,1/5,1/6,1/7,1/8,1/9]; %可供选取的成对比值
L=length(P);
A=ones(n,n);
number=1500; %模拟次数
R=0;
for kp=1:number %获得一个成对比较矩阵
for i=1:n-1
for j=i+1:n
k=floor(1+L*rand(1,1));
A(i,j)=P(k); %得到一个随机的成对值
A(j,i)=1/P(k);
End
End
lam=max(elg(A)); %求最大特征值
CI=(lam-n)/(n-1);
R=R+CI;
End
PI=R/number;
Fprintf(‘n=%2d,PI=%6.3f\n’,n,RI);
对于n≥3的成对比较矩阵A一致性比率CR=CI/CR＜0.1,则A的不一致性可容忍。
论文中要给出成对比较矩阵、最大特征值和它对应的特征向量，以及小于0.1的CR。
从目标层到方案层（组合权向量和组合一致性的检验）
用同样的方法，构造每个方案对准则层的每一个成对比较矩阵，求出相应权重，看此方案是否合理
单片机
LED
符号为
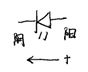工作是有方向性的，分阴阳两极，电源的正极需接到阳极，负极接阴。
只要将高电平改为低电平，正负极通电，LED点亮。
Led模块连接P2系列端口，P20到P27共八个，为高电平，值为1，如此使得led不亮
P20=1 P2=ff（16进制）或1111 1111（二进制）对应八个（注意是倒数）
注意P20写作p2^0。
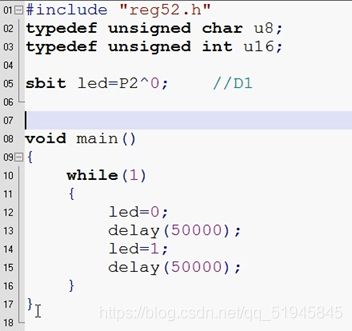
#include “reg52.h” //单片机需要的头文件
Void main() //主函数
{
while(1) //无限循环使程序能不断工作
{
}
}
延时
首先需要Typedef定义无符号字节
接下来定义数值就可以如 u8 i；
LED闪烁
常用预处理命令
#define
#define A P0(注意后面不加分号)
定义端口P0为A，便于在修改时可以快速修改端口
循环左移右移函数
包含在instrins.h库函数里
_crol_(a,b)左移
_cror_(a,b)右移，a为移值，b为位数
左右移的本质
电平值 1110➡1101➡1011
注意左右移动要加延时
右侧点击此头文件可以查看此函数库的所有函数
蜂鸣器
分为无源蜂鸣器（背部有电路板），压电式，需要输入一定频率的脉冲。
有源蜂鸣器，电磁式，只需输电平并通过放大电路放大驱动电流。
改变输出波形的频率可以调整音调，改变输出电平的高低电平占空比（高电平占一个电平周期的时间比），则可以控制蜂鸣器的声音大小
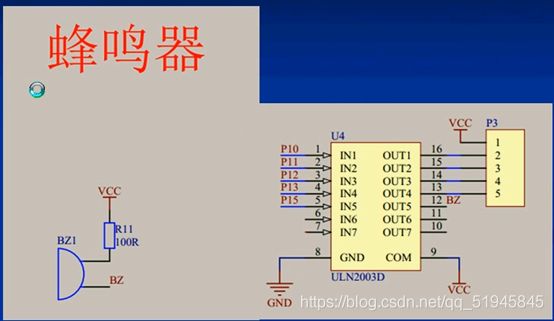
P15➡ULN2003D芯片➡BZI无源蜂鸣器
ULN2003是大电流驱动阵列，放大电流，可直接驱动蜂鸣器、继电器等负载。
Sbit beep=P1^5; 定义p15引脚
单片机上的是无源蜂鸣器，需要给脉冲，给高低电平的不断变化周期即可，可以通过定义延时实现
beep=~beep;(取反)转换高低电平。
频率=1/延时*2
