详解归并排序算法

基本思想

归并排序的基本思想是：
先将序列一次次分成子序列，直到子序列长度为1；
再将已有序的子序列合并，得到完全有序的序列。
可以看出归并排序运用了 分而治之的思想 。

例子

输入数组 [ 2, 5, 3 , 10, -3, 1 , 6 , 4]；
初始状态如下：

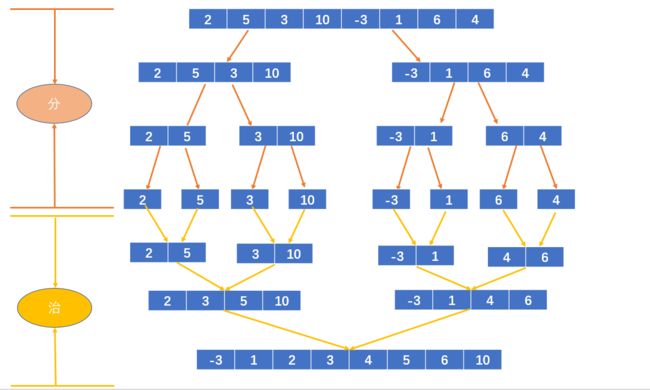
分治思想如下：
首先把数组依次折半，分成小的子数组，直到每一个子数组的长度都为1；
然后合并子数组，在合并的过程中进行排序；
如下图：

将数组分成子数组的方法比较简单，不过多介绍；
下面介绍一下合并操作,以最后一次合并为例：
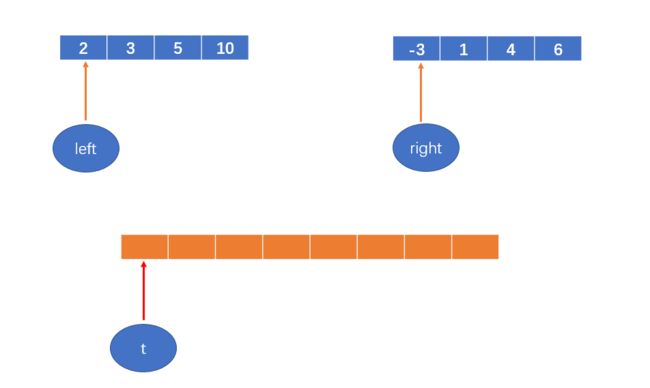
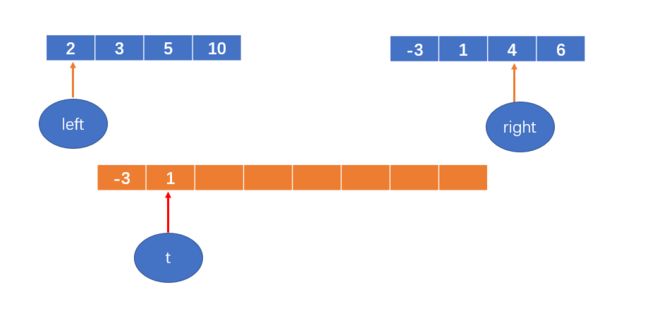
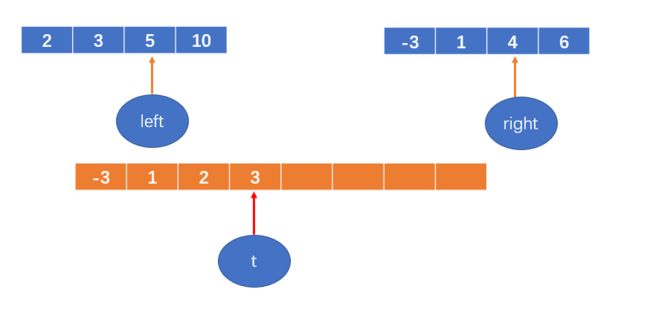
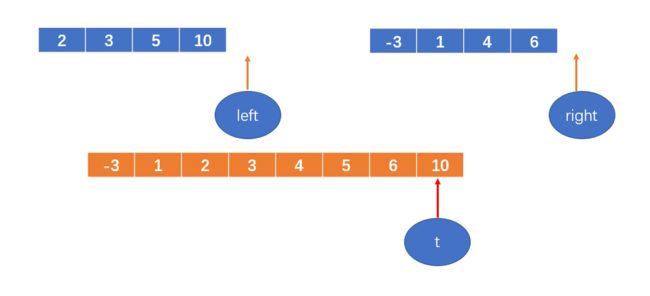
下图是最后一次合并前的两个数组：

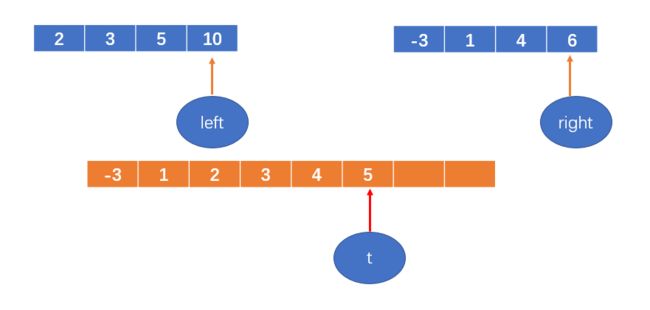
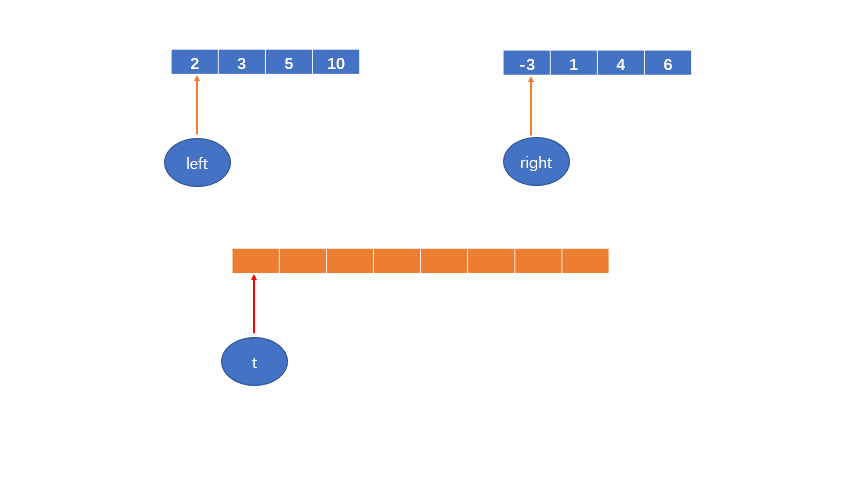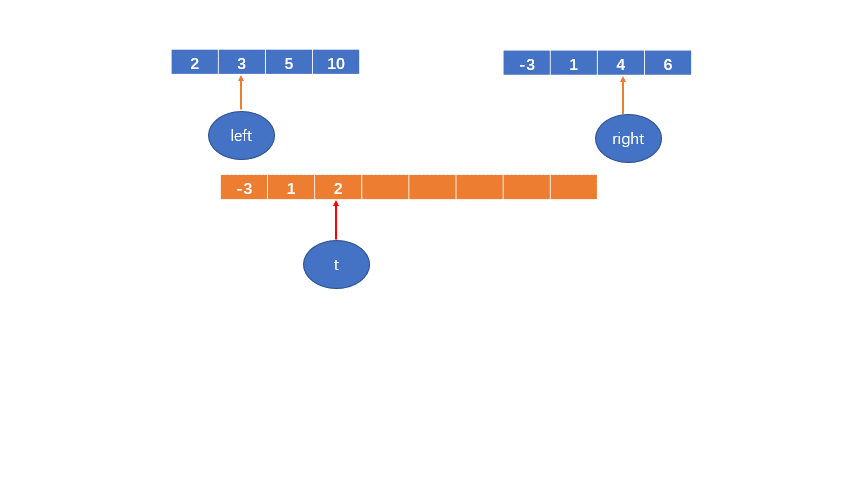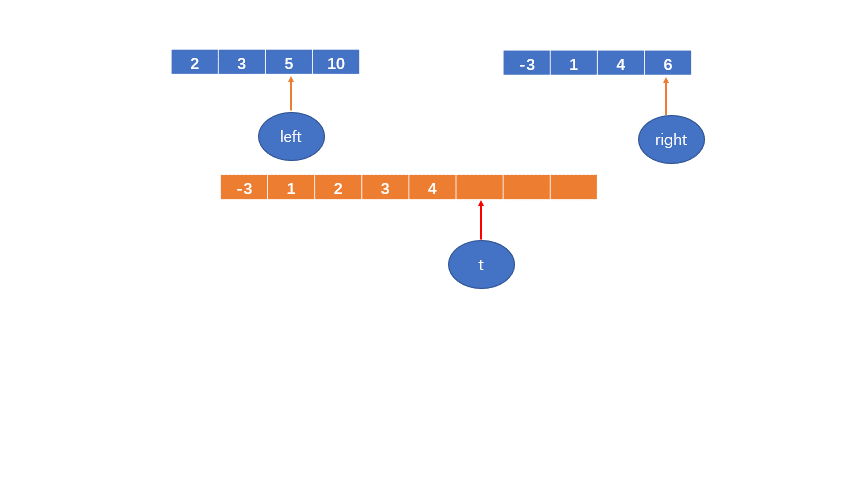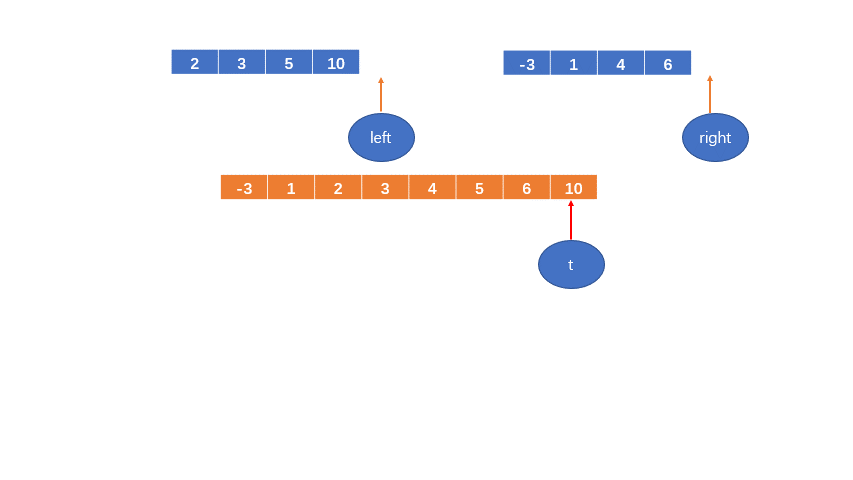
定义两个变量 left和right，分别赋值为两个数组的首元素的索引；
初始化一个数组，数组长度为原数组大小；
再定义一个变量，t，初始化为新开的数组的第一个元素的索引，即0；
如下图：

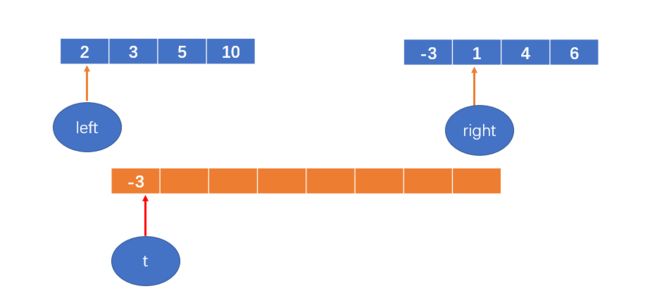
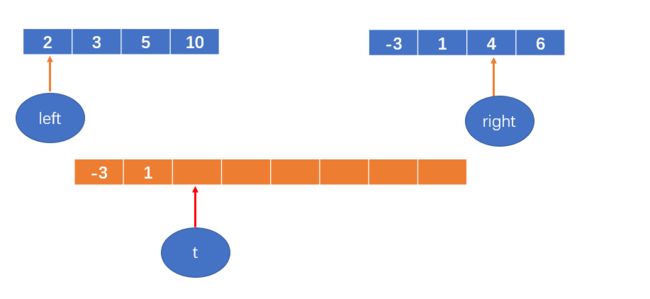
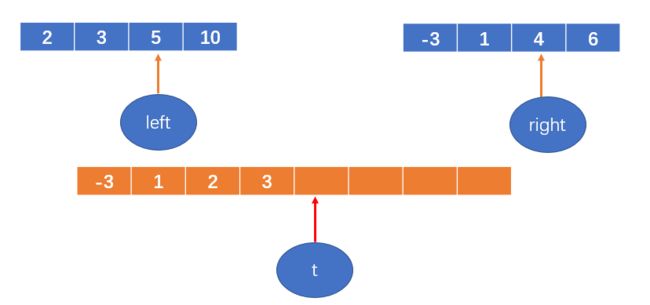
然后每次从两个数组中找相对较小的数，填到新开的数组中；

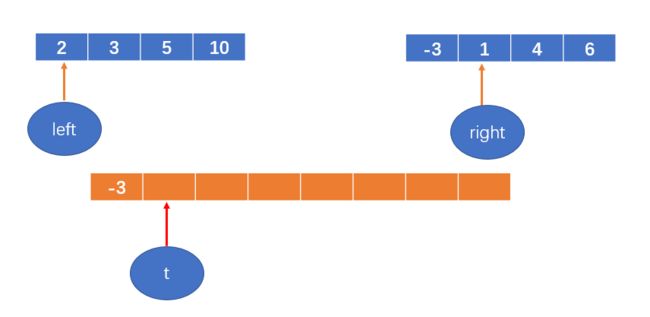
-3 < 2，将-3填到数组中，right++;

t++;

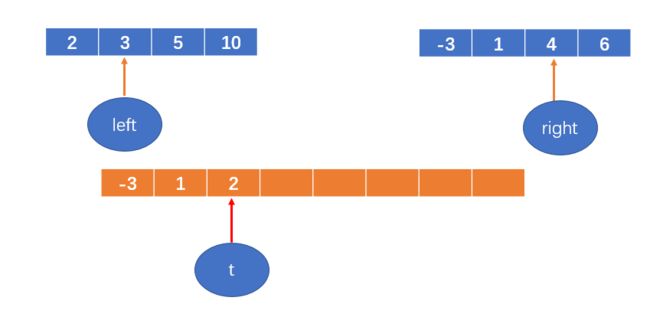
1< 2，将1填到数组中，right++;

t++;

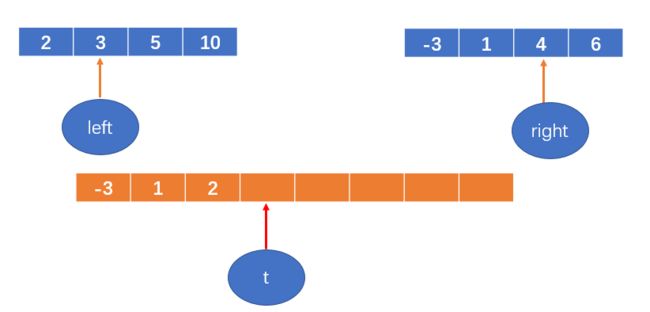
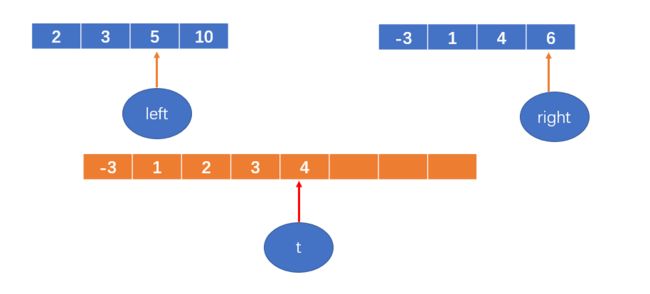
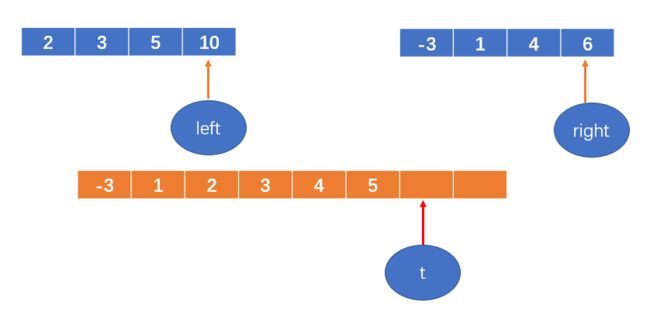
2 < 4，将2填到数组中，left++;

t++

3 < 4，将3填到数组中，left++;

t++

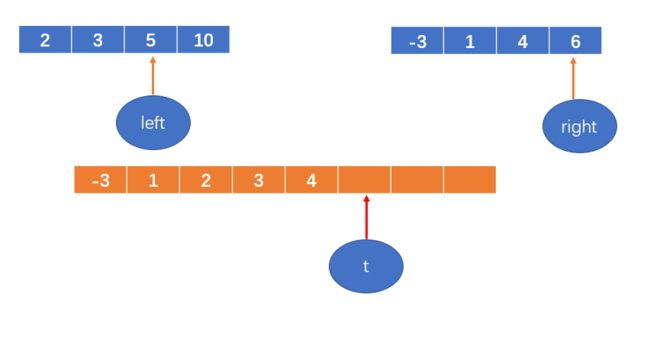
4 < 5，将4填到数组中，right++;

t++

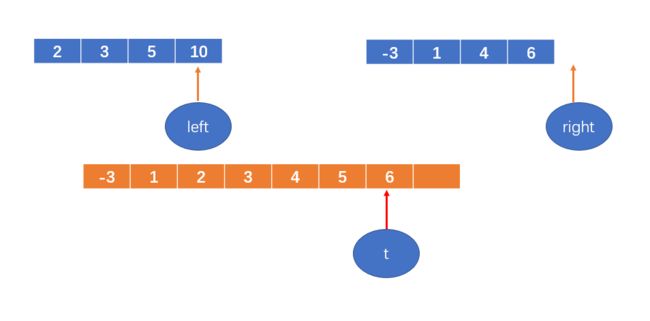
5 < 6，将5填到数组中，left++;

t++

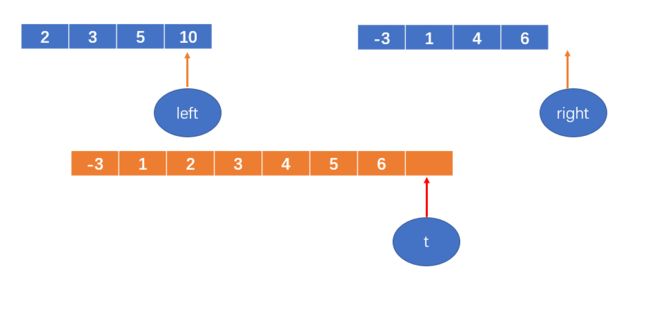
6 < 10，将6填到数组中，right++后越界

t++

再把剩余的数加到数组里，直到子数组中的数都填过来；

动图如下：

代码

注意：
代码中的right和例子中的right含义不同；
具体含义见代码参数注释。
先来看合并子数组的代码；
函数声明如下：

    //合并的方法
    /**
     *
     * @param arr 待排序的数组
     * @param left 左边序列的初始索引
     * @param mid 中间索引（用来判断左边序列何时结束：到mid结束，右边序列何时开始，即mid+1）
     * @param right 右边数组结束的索引
     * @param temp 临时存储的数组
     */
public static void merge(int[] arr, int left, int mid, int right, int[] temp){
	
}

然后是合并的方法

public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
		//左边有序序列的初始索引
        int i = left; 
        //右边有序序列的初始索引
        int j = mid + 1; 
        int t = 0; // 指向临时数组的当前索引
        //将两边数组的元素进行比较，依次填进临时数组
        //直到将一边填完
        while (i <= mid && j <= right) {
        //选择较小的添加进去
            if(arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t += 1;
                i += 1;
            } else { 
                temp[t] = arr[j];
                t += 1;
                j += 1;
            }
        }
        
        //把有剩余数据的数组全部填充到数组
        //肉眼可以判别哪个有数据，但是计算机需要用循环条件判别
        //所以有两个while循环
        while( i <= mid) {
            temp[t] = arr[i];
            t += 1;
            i += 1;
        }

        while( j <= right) { 
            temp[t] = arr[j];
            t += 1;
            j += 1;
        }
        
        //将temp数组的元素拷贝到arr
        t = 0;
        int Left = left; 
        while(Left <= right) {
            arr[Left] = temp[t];
            t += 1;
            Left += 1;
        }
    }

归并代码:

 //归并（分+治）方法
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if(left < right) {
            int mid = (left + right) / 2; //中间索引
            //左边递归分解
            mergeSort(arr, left, mid, temp);
            //右边递归分解
            mergeSort(arr, mid + 1, right, temp);
            //合并
            merge(arr, left, mid, right, temp);
        }
    }

全代码

import java.util.Arrays;

public class Solution {
    public static void main(String[] args) {
        int []arr= new int[]{2,5,3,10,-3,1,6,4};
        int []temp = new int[arr.length];
        mergeSort(arr,0,arr.length-1,temp);
        System.out.println(Arrays.toString(arr));
    }

    //归并（分+治）方法
    public static void mergeSort(int[] arr, int left, int right, int[] temp) {
        if(left < right) {
            int mid = (left + right) / 2; //中间索引
            //左边递归分解
            mergeSort(arr, left, mid, temp);
            //右边递归分解
            mergeSort(arr, mid + 1, right, temp);
            //合并
            merge(arr, left, mid, right, temp);
        }
    }

    //合并的方法
    /**
     *
     * @param arr 排序的原始数组
     * @param left 左边有序序列的初始索引
     * @param mid 中间索引
     * @param right 右边索引
     * @param temp 做中转的数组
     */
    public static void merge(int[] arr, int left, int mid, int right, int[] temp) {
        //左边有序序列的初始索引
        int i = left;
        //右边有序序列的初始索引
        int j = mid + 1;
        int t = 0; // 指向临时数组的当前索引
        //将两边数组的元素进行比较，依次填进临时数组
        //直到将一边填完
        while (i <= mid && j <= right) {
            //选择较小的添加进去
            if(arr[i] <= arr[j]) {
                temp[t] = arr[i];
                t += 1;
                i += 1;
            } else {
                temp[t] = arr[j];
                t += 1;
                j += 1;
            }
        }

        //把有剩余数据的数组全部填充到数组
        //肉眼可以判别哪个有数据，但是计算机需要用循环条件判别
        //所以有两个while循环
        while( i <= mid) {
            temp[t] = arr[i];
            t += 1;
            i += 1;
        }

        while( j <= right) {
            temp[t] = arr[j];
            t += 1;
            j += 1;
        }

        //将temp数组的元素拷贝到arr
        t = 0;
        int Left = left;
        while(Left <= right) {
            arr[Left] = temp[t];
            t += 1;
            Left += 1;
        }
    }
}

时间复杂度

归并排序的是按照分层进行比较的，会分成$lo{g}_{2}n$层；
而每一层的比较次数为$O(n)$；
所以时间复杂度求得$O(nlogn)$。

稳定性

在交换元素时，可以限定元素相等时不移动，所以归并排序是可以稳定的。

欢迎关注

扫下方二维码即可关注: