第十二届蓝桥杯 2021年国赛真题 (Java 大学A组)

---

  二十九号考马原，等到二十八号再背，

  更新中。。。

---

#A 纯质数

本题总分：5 分

---

问题描述

  如果一个正整数只有 $1$ 和它本身两个约数，则称为一个质数（又称素数）。
  前几个质数是：$2,3,5,7,11,13,17,19,23,29,31,37,\cdot \cdot \cdot$ 。
  如果一个质数的所有十进制数位都是质数，我们称它为纯质数。例如：$2,3,5,7,23,37$ 都是纯质数，而 $11,13,17,19,29,31$ 不是纯质数。当然 $1,4,35$ 也不是纯质数。
  请问，在 $1$ 到 $20210605$ 中，有多少个纯质数？

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

1903

---

按序枚举

---

  一种朴素的想法，在打表 $[1,20210605]$ 间的质数时，额外的进行一次纯质数效验，并将结果累加起来。

import java.util.ArrayList;
import java.util.List;

public class Test {

    public static final int N = 20210605;

    public static void main(String[] args) {
        boolean[] marked = new boolean[N + 1];
        List<Integer> primes = new ArrayList();
        marked[0] = marked[1] = true;
        int ans = 0;
        for (int i = 2; i <= N; i++) {
            if (!marked[i]) {
                primes.add(i);
                boolean flag = false;
                for (int k = i; k > 0; k /= 10)
                    if (flag = marked[k % 10]) break;
                if (!flag) ans++;
            }
            for (int p : primes) {
                if (p * i > N)  break;
                marked[p * i] = true;
                if (i % p == 0) break;
            }
        }
        System.out.println(ans);
    }
}

---

按位枚举

---

  在朴素的解法中，我们会发现，很多拆分判断一个质数是否是纯质数是没有必要的，因为在 $[0,10)$ 中，质数仅占 $\{2,3,5,7\}$ 四位，如果仅判断这四个数字组合成的数是否是质数的话，性能能否有进一步的提升呢？

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;

public class Test {

    public static final int N = 20210605;

    public static int[][] digits = new int[8][4];

    public static void main(String[] args) {
        boolean[] primes = new boolean[N + 1];
        List<Integer> helper = new ArrayList();
        Arrays.fill(primes, 2, N, true);
        int ans = 0;
        for (int i = 2; i <= N; i++) {
            if (primes[i]) helper.add(i);
            for (int p : helper) {
                if (p * i > N)  break;
                primes[p * i] = false;
                if (i % p == 0) break;
            }
        }
        digits[0] = new int[]{2, 3, 5, 7};
        for (int k = 1; k < 7; k++)
            for (int i = 0; i < 4; i++)
                digits[k][i] = digits[k - 1][i] * 10;
        digits[7] = new int[]{ digits[6][0] * 10 };
        System.out.println(dfs(primes, 0, 0));
    }

    public static int dfs(boolean[] primes, int k, int depth) {
        if (depth == 8) return k <= N && primes[k] ? 1 : 0;
        int ans = primes[k] ? 1 : 0;
        for (int a : digits[depth])
            ans += dfs(primes, k + a, depth + 1);
        return ans;
    }
}

  实际上性能并没有进一步的提升，并且代码量还有所增加。

  这是因为在 $(1,N]$ 这个范围中的质数大约有 $\frac{N}{\ln N}$ 个，而按位组成的可能是纯质数的数大约有 $4^{\ln N}$ 个，这显然不是一个增值量级的。

---

#B 完全日期

本题总分：5 分

---

问题描述

  如果一个日期中年月日的各位数字之和是完全平方数，则称为一个完全日期。
  例如：$2021$ 年 $6$ 月 $5$ 日的各位数字之和为 $2+0+2+1+6+5=16$，而 $16$ 是一个完全平方数，它是 $4$ 的平方。所以 $2021$ 年 $6$ 月 $5$ 日是一个完全日期。
  例如：$2021$ 年 $6$ 月 $23$ 日的各位数字之和为 $2+0+2+1+6+2+3=16$，是一个完全平方数。所以 $2021$ 年 $6$ 月 $23$ 日也是一个完全日期。
  请问，从 $2001$ 年 $1$ 月 $1$ 日到 $2021$ 年 $12$ 月 $31$ 日中，一共有多少个完全日期？

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

977

---

Java党的完全胜利

---

  LocalDate好用。

---

朴素解法

---

  枚举 $[2001$-$01$-$01$，$2021$-$12$-$31]$ 这个区间间内的时间，判断然后累加。

import java.time.LocalDate;

public class Test {

    public static final int maxPerfect = 2 + 0 + 1 + 9 + 0 + 9 + 2 + 9;

    public static final boolean[] perfect = new boolean[maxPerfect + 1];

    public static LocalDate start = LocalDate.of(2001, 01, 01);

    public static LocalDate end = LocalDate.of(2021, 12, 31);

    public static void main(String[] args) {
        int count = 0;
        for (int i = 1; i * i<= maxPerfect; i++)
            perfect[i * i] = true;
        while (end.compareTo(start) >= 0) {
            if (perfect[calc(start)])
                count++;
            start = start.plusDays(1);
        }
        System.out.println(count);
    }

    public static int calc(LocalDate date) {
        String dateStr = date.toString();
        int res = 0;
        for (int i = dateStr.length() - 1; i >= 0; i--)
            if (Character.isDigit(dateStr.charAt(i)))
                res += Character.digit(dateStr.charAt(i), 10);
        return res;
    }
}

---

朴素改进

---

  在 $[2001$-$01$-$01$，$2021$-$12$-$31]$ 中，各数位之和不仅存在最大值 $2+0+1+9+0+9+2+9=32$，还存在有最小值 $2+0+0+1+0+1+0+1$，也就是说，可能的完全平方数，不外乎 $3\times 3$、$4\times 4$、$5\times 5$ 三个，就这一点我们来简化我们的代码。

import java.time.LocalDate;

public class Test {

    public static LocalDate start = LocalDate.of(2001, 01, 01);

    public static LocalDate end = LocalDate.of(2021, 12, 31);

    public static void main(String[] args) {
        int count = 0;
        while (end.compareTo(start) >= 0) {
            if (isPerfect(start)) count++;
            start = start.plusDays(1);
        }
        System.out.println(count);
    }

    public static boolean isPerfect(LocalDate date) {
        String dateStr = date.toString();
        int sum = 0;
        for (int i = dateStr.length() - 1; i >= 0; i--)
            if (Character.isDigit(dateStr.charAt(i)))
                sum += Character.digit(dateStr.charAt(i), 10);
        return sum == 3 * 3 || sum == 4 * 4 || sum == 5 * 5;
    }
}

---

不依赖 API 的实现

---

  先统计出平年月份和日期各数位之和的出现次数，然后遍历年份时额外的判断一道是否为闰年。

public class Test {

    public static void main(String[] args) {
        int[] bigMonth = { 1, 3, 5, 7, 8, 1 + 0, 1 + 2 };
        int[] smallMonth = { 4, 6, 9, 1 + 1 };
        int[] calendar = new int[9 + 2 + 9 + 1];
        int ans = 0;
        for (int day = 1; day <= 31; day++)
            for (int month : bigMonth)
                calendar[month + calc(day)]++;
        for (int day = 1; day <= 30; day++)
            for (int month : smallMonth)
                calendar[month + calc(day)]++;
        for (int day = 1; day <= 28; day++)
            calendar[2 + calc(day)]++;
        for (int year = 2001; year <= 2021; year++) {
            if (isLeapYear(year))
                if (isLeapYear(year + 2 + 2 + 9)) ans++;
            for (int i = 0; i < calendar.length; i++) {
                if (calendar[i] == 0) continue;
                if (isPerfect(calc(year) + i))
                    ans += calendar[i];
            }
        }
        System.out.println(ans);
    }

    public static int calc(int n) {
        int res = 0;
        do
            res += n % 10;
        while ((n /= 10) > 0);
        return res;
    }

    public static boolean isPerfect(int num) { return num == 3 * 3 || num == 4 * 4 || num == 5 * 5; }

    public static boolean isLeapYear(int year) { return year % 100 == 0 ? year % 400 == 0 : year % 4 == 0; }
}

---

#C 最小权值

本题总分：10 分

---

问题描述

  对于一棵有根二叉树 $T$，小蓝定义这棵树中结点的权值 $W(T)$ 如下：
  空子树的权值为 $0$。
  如果一个结点 $v$ 有左子树 $L$, 右子树 $R$，分别有 $C(L)$ 和 $C(R)$ 个结点，则 $W(v)=1+2W(L)+3W(R)+(C(L){)}^{2}C(R)$。
  树的权值定义为树的根结点的权值。
  小蓝想知道，对于一棵有 $2021$ 个结点的二叉树，树的权值最小可能是多少？

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

2653631372

---

动态规划

---

  根据题意，显然有 $N=2021$，$W(0)=0$，$W(N)=\min \{1+2W(L)+3W(R)+(C(L){)}^{2}C(R)\}$，其中 $L+R=N-1$，$0\le L\le R\le N$。

  状态转移方程就在脸上：$$dp(y)=\{\begin{array}{lr}0& i=0\\ \min \{1+2dp(l)+3dp(r)+l^{2}r\}& l+r=i-1，0\le l\le r\le i\end{array}$$  也是道签到题。

public class Test {

    public static final int N = 2021;

    public static void main(String[] args) {
        long[] dp = new long[N + 1];
        for (int i = 1; i <= N; i++) {
            dp[i] = Long.MAX_VALUE;
            for (int l = i >> 1; l >= 0; l--)
                dp[i] = Math.min(dp[i],
                    1 + 2 * dp[l] + 3 * dp[i - l - 1] + l * l * (i - l - 1));
        }
        System.out.println(dp[N]);
    }
}

---

#D 覆盖

本题总分：10 分

---

问题描述

  小蓝有一个国际象棋的棋盘，棋盘的大小为 $8\times 8$，即由 $8$ 行 $8$ 列共 $64$ 个方格组成。棋盘上有美丽的图案，因此棋盘旋转后与原来的棋盘不一样。
  小蓝有很多相同的纸片，每张纸片正好能覆盖棋盘的两个相邻方格。小蓝想用 $32$ 张纸片正好将棋盘完全覆盖，每张纸片都覆盖其中的两个方格。
  小蓝发现，有很多种方案可以实现这样的覆盖。如果棋盘比较小，方案数相对容易计算，比如当棋盘是 $2\times 2$ 时有两种方案，当棋盘是 $4\times 4$ 时有 $36$ 种方案。但是小蓝算不出他自己的这个 $8\times 8$ 的棋盘有多少种覆盖方案。
  请帮小蓝算出对于这个 $8\times 8$ 的棋盘总共有多少种覆盖方案。

---

答案提交

  这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

12988816

---

变种八皇后

---

  不知道怎么分类，

  但小规模的完全摆放问题都可以照八皇后的板子做。

public class Test {

    public static void main(String[] args) { new Test().run(); }

    int N = 8, ans = 0;

    boolean[][] marked = new boolean[N][N];

    void run() {
        dfs(0, 0);
        System.out.println(ans);
    }

    void dfs(int x, int y) {
        if (x == N) ans++;
        else if (marked[x][y]) {
            if (y == N - 1) dfs(x + 1, 0);
            else dfs(x, y + 1);
        } else {
            marked[x][y] = true;
            if (y + 1< N && !marked[x][y + 1]) {
                marked[x][y + 1] = true;
                dfs(x, y + 1);
                marked[x][y + 1] = false;
            }
            if (x + 1< N && !marked[x + 1][y]) {
                marked[x + 1][y] = true;
                dfs(x, y);
                marked[x + 1][y] = false;
            }
            marked[x][y] = false;
        }
    }
}

  稍微说明一下第 $28$ 行，

  其实是复用了第 $17$ 行的这个 $\mathrm{i}\mathrm{f}$，

  偷个小懒。

---

状压 DP

---

  自然地去思考用一串二进制描述一行，

  大致就是 $0/1$ 表示该位置为 横 $/$ 竖 覆盖纸片的一半，

  容易知道，$0$ 必须呈偶数个连续，即横覆盖纸片必须完整，

  上一行的 $1$ 与下一行的 $1$ 必须一一对应，即相邻两行必须满足 $\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}[\mathrm{i}-1]\&\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}[\mathrm{i}]=\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}[\mathrm{i}-1]$，

  转移后的行状态改为 $\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}[\mathrm{i}]-\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}[\mathrm{i}-1]$，即取出不完整的竖覆盖纸片。

  整个算法复杂度在 $O(N{4}^N)$，

  当然我称它为 “自然” 是有原因的，

  因为还有总较为反常的思路，当然你也可以用上述状压优化的方式去思考它。

  具体地说：

  一个方格必然会被四种纸片覆盖：竖摆上、竖摆下、横摆左、横摆右。

  对于每一行，我们使用 $1$ 表示横着摆放的纸片的上半部分，$0$ 则表示其他三种情况。

  容易知道，每次转移必须满足

  $\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}[\mathrm{i}-1]\&\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}[\mathrm{i}]=0$

  $\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}[\mathrm{i}-1]\mid \mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}[\mathrm{i}]$ 中 $0$ 呈偶数个连续。

  使用这种思路可以少做一次减法，

  略微优化了一点点。

public class Test {

    static int N = 8, M;

    public static void main(String[] args) {
        int[][] dp = new int[2][M = 1 << N];
        boolean[] check = new boolean[M];
        boolean flag, even;
        for (int i = 0; i < M; i++) {
            flag = even = true;
            for (int j = 0; j < N; j++)
                if ((i >> j & 1) == 0) even = !even;
                else {
                    flag &= even;
                    even = true;
                }
            check[i] = flag & even;
        }
        dp[0][0] = 1;
        for (int i = 1; i <= N; i++)
            for (int j = 0; j < M; j++) {
                dp[i & 1][j] = 0;
                for (int k = 0; k < M; k++)
                    if ((j & k) == 0 && check[j | k])
                        dp[i & 1][j] += dp[(i - 1) & 1][k];
            }
        System.out.println(dp[N & 1][0]);
    }
}

#E 123

时间限制: $5.0$s 内存限制: $512.0$MB 本题总分：$15$分

---

问题描述

  小蓝发现了一个有趣的数列，这个数列的前几项如下：
  $1,1,2,1,2,3,1,2,3,4,...$
  小蓝发现，这个数列前 $1$ 项是整数 $1$，接下来 $2$ 项是整数 $1$ 至 $2$，接下来 $3$ 项是整数 $1$ 至 $3$，接下来 $4$ 项是整数 $1$ 至 $4$，依次类推。
  小蓝想知道，这个数列中，连续一段的和是多少。

---

输入格式

  输入的第一行包含一个整数 $T$，表示询问的个数。
  接下来 $T$ 行，每行包含一组询问，其中第 $i$ 行包含两个整数 $l_i$ 和 $r_i$，表示询问数列中第 $l_i$ 个数到第 $r_i$ 个数的和。

---

输出格式

  输出 $T$ 行，每行包含一个整数表示对应询问的答案。

---

测试样例₁

Input：
3
1 1
1 3
5 8

Output：
1
4
8

---

评测用例规模与约定

  对于 $10$% 的评测用例，$1\le T\le 30,1\le l_i\le r_i\le 100$。
  对于 $20$% 的评测用例，$1\le T\le 100,1\le l_i\le r_i\le 1000$。
  对于 $40$% 的评测用例，$1\le T\le 1000,1\le l_i\le r_i\le 10^6$。
  对于 $70$% 的评测用例，$1\le T\le 10000,1\le l_i\le r_i\le 10^9$。
  对于 $80$% 的评测用例，$1\le T\le 1000,1\le l_i\le r_i\le 10^{12}$。
  对于 $90$% 的评测用例，$1\le T\le 10000,1\le l_i\le r_i\le 10^{12}$。
  对于所有评测用例，$1\le T\le 100000,1\le l_i\le r_i\le 10^{12}$。

---

前缀和

---

  区间和问题，一般先考虑的都是使用前缀和，但这里给出的区间范围太大，以至于用全部的内存来存放前缀和，能通过的用例可能也只有半数，因此这里要将原序列$$[\text{[}[1,1,2,1,2,3,1,\cdots ,n-1,n]\text{]}]$$变形为矩阵$$\left[\begin{array}{ccccc}1& & & & \\ 1& 2& & & \\ 1& 2& 3& & \\ ⋮& ⋮& ⋮& \ddots & \\ 1& 2& 3& \cdots & n\end{array}\right]$$为了能涵盖 $[1,10^{12}]$ 间的查询，即矩阵包含 $10^{12}$ 个元素，这里 $n$ 取 $n=\sqrt{2E12}$。

  对于序列变形的矩阵，我们分别求出列与最后一行的前缀和后，组合起来就能在对数时间内 (需要二分查找给定 k 所在的行) 得到任意 $[1,k]$，$k\in [1，10^{12}]$ 间内的元素和，对于任意 ${\sum }_{i=l}^r{a}_i$，我们只需转换为 ${\sum }_{i=1}^r{a}_i-{\sum }_{i=1}^{l-1}{a}_i$ 问题就被解决了。

  还有就是溢出问题，形如这种矩阵，在最大元素为 $n$ 时，其矩阵元素和为 $n+2(n-1)+3(n-2)+\cdots +n$ 。
  $=n(1+2+3+\cdots +n)-n(1\times 2+2\times 3+3\times 4+\cdots +(n-1)n)$
  $=\frac{n^2(n-1)}{2}-(1^2+1+2^2+2+3^2+\cdots +(n-1{)}^2+n-1)$
  $=\frac{n^2(n-1)}{2}-\{(1^2+2^2+3^2+\cdots +(n-1{)}^2)+(1+2+3+\cdots +n-1)\}$
  $=\frac{n^2(n-1)}{2}-\frac{n(n-1)(2n-1)}{6}-\frac{n(n-1)}{2}$

  取 $n$ 为 $\sqrt{2E12}$，矩阵元素和约为 $4.7E17$，长整形够用。

import java.io.*;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    int N = (int)Math.sqrt(2E12) + 1;
    long[] row = new long[N + 1], col = new long[N + 1];

    void run() {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out);
        for (int i = 1; i <= N; i++) {
            row[i] = i + row[i - 1];
            col[i] = col[i - 1] + row[i];
        }
        int T = in.readInt();
        long l, r;
        while (T-- > 0) {
            l = in.readLong();
            r = in.readLong();
            out.println(sum(r) - sum(l - 1));
        }
        out.flush();
    }

    long sum(long r) {
        int k = lowerBound(r);
        return r == row[k] ? col[k] : col[k - 1] + row[(int)(r - row[k - 1])];
    }

    int lowerBound(long k) {
        int offset = 0, length = N + 1;
        while (length > 0) {
            int half = length >> 1;
            if (k > row[offset + half]) {
                offset += half + 1;
                length -= half + 1;
            } else length = half;
        }
        return offset;
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }

        long readLong() { return Long.parseLong(read()); }
    }
}

---

#F 二进制问题

时间限制: $1.0$s 内存限制: $512.0$MB 本题总分：$15$ 分

---

问题描述

  小蓝最近在学习二进制。他想知道 $1$ 到 $N$ 中有多少个数满足其二进制表示中恰好有 $K$ 个 $1$。你能帮助他吗？

---

输入格式

  输入一行包含两个整数 $N$ 和 $K$。

---

输出格式

  输出一个整数表示答案。

---

测试样例₁

Input：
7 2

Output：
3

---

评测用例规模与约定

  对于 $30$% 的评测用例，$1\le N\le 10^6,1\le K\le 10$。
  对于 $60$% 的评测用例，$1\le N\le 2\times 10^9,1\le K\le 30$。
  对于所有评测用例，$1\le N\le 10^{18},1\le K\le 50$。

---

组合数学

---

  若 $N$ 恰等于 $2^k-1$，$k\in {\mathbb{Z}}^{+}$，答案显然等于 $C_{\lfloor {\log }_{2}N\rfloor }^K$，

  因此我们可以将 $[1,N]$ 拆分成 $[1,2^k)$、$[2^k,N]$ 两部分，并使得 $k$ 最大，而 $[2^k,N]$ 可以转换成 $[0,N-2^k]$ 中有多少个数二进制表示中恰好有 $K-1$ 个 $1$ 问题。

  可以数位 $\mathrm{D}\mathrm{P}$，但没必要。

import java.util.Scanner;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        Scanner in = new Scanner(System.in);
        long N = in.nextLong(), ans = 0;
        int K = in.nextInt();
        for (int k = 63; k >= 0; k--)
            if ((N >> k & 1) == 1) {
                ans += C(k, K--);
                if (K == 0) { ans++; break;}
            }
        System.out.println(ans);
    }

    long[][] C = new long[65][65];

    long C(int n, int m) {
        if (m > n) return 0;
        if (n == 0 || m == 0 || n == m) return 1;
        if (C[n][m] != 0) return C[n][m];
        return C[n][m] = C(n - 1, m - 1) + C(n - 1, m);
    }
}

  可以说，非常简单。

---

#G 冰山

时间限制: $5.0$s 内存限制: $512.0$MB 本题总分：$20$ 分

---

问题描述

  一片海域上有一些冰山，第 $i$ 座冰山的体积为 $V_i$。
  随着气温的变化，冰山的体积可能增大或缩小。第 $i$ 天，每座冰山的变化量都是 $X_i$。当 $X_i>0$ 时，所有冰山体积增加 $X_i$；当 $X_i<0$ 时，所有冰山体积减少 $-X_i$；当 $X_i=0$ 时，所有冰山体积不变。
  如果第 $i$ 天某座冰山的体积变化后小于等于 $0$，则冰山会永远消失。
  冰山有大小限制 $k$。如果第 $i$ 天某座冰山 $j$ 的体积变化后 $V_j$ 大于 $k$，则它会分裂成一个体积为 $k$ 的冰山和 $V_j-k$ 座体积为 $1$ 的冰山。
  第 $i$ 天结束前（冰山增大、缩小、消失、分裂完成后），会漂来一座体积为 $Y_i$ 的冰山（$Y_i=0$ 表示没有冰山漂来）。
  小蓝在连续的 $m$ 天对这片海域进行了观察，并准确记录了冰山的变化。小蓝想知道，每天结束时所有冰山的体积之和（包括新漂来的）是多少。
  由于答案可能很大，请输出答案除以 $998244353$ 的余数。

---

输入格式

  输入的第一行包含三个整数 $n,m,k$，分别表示初始时冰山的数量、观察的天数以及冰山的大小限制。
  第二行包含 $n$ 个整数 $V_1,V_2,\cdot \cdot \cdot ,V_n$，表示初始时每座冰山的体积。
  接下来 $m$ 行描述观察的 $m$ 天的冰山变化。其中第 $i$ 行包含两个整数 $X_i,Y_i$，意义如前所述。

---

输出格式

  输出 $m$ 行，每行包含一个整数，分别对应每天结束时所有冰山的体积之和除以 $998244353$ 的余数。

---

测试样例₁

Input：
1 3 6
1
6 1
2 2
-1 1

Output：
8
16
11

Explanation：
在本样例说明中，用 [a1, a2, · · · , an] 来表示每座冰山的体积。
初始时的冰山为 [1]。
第 1 天结束时，有 3 座冰山：[1, 1, 6]。
第 2 天结束时，有 6 座冰山：[1, 1, 2, 3, 3, 6]。
第 3 天结束时，有 5 座冰山：[1, 1, 2, 2, 5]。

---

评测用例规模与约定

  对于 $40$% 的评测用例，$n,m,k\le 2000$；
  对于 $60$% 的评测用例，$n,m,k\le 20000$；
  对于所有评测用例，$1\le n,m\le 100000,1\le k\le 10^9,1\le V_i\le k,0\le Y_i\le k,-k\le X_i\le k$。

---

Splay

---

  $\mathrm{s}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{y}$ 上打个 $\mathrm{l}\mathrm{a}\mathrm{z}\mathrm{y}$ 做冰山的变化就行了，

  具体的我们维护一颗 $\mathrm{s}\mathrm{p}\mathrm{l}\mathrm{a}\mathrm{y}$，

  树上每个节点 $<key,cnt>$ 表示大小为 $\mathrm{k}\mathrm{e}\mathrm{y}$ 的冰山共有 $\mathrm{c}\mathrm{n}\mathrm{t}$ 座，$X<0$ 时将 $key$ 为 $-X$ 的节点选择至根节点 ，然后删除根节点做子树，$X>0$ 也如法炮制，不过我们在维护节点信息时需要额外维护 $size$ 来降低计算分裂出的冰山个数的时间复杂程度。

import java.io.*;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    int p = 998244353;

    void run() {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out);
        int n = in.readInt(), m = in.readInt(), k = in.readInt();
        Splay tree = new Splay(n + 3 * m);
        while (n-- > 0)
            tree.add(in.readInt(), 1);
        while (m-- > 0) {
            int X = in.readInt(), Y = in.readInt();
            if (X != 0) {
                tree.updateAll(X);
                if (X < 0) tree.deleteFloor(1);
                else tree.f(tree.deleteHigher(k), k);
            }
            if (Y != 0)
                tree.add(Y, 1);
            out.println(tree.V());
        }
        out.flush();
    }

    class Splay {

        int root, cur;

        int[] father, children[];

        int[] cnt, lazy, size, V;

        long[] key;

        Splay(int maxSize) {
            father = new int[maxSize + 1];
            children = new int[maxSize + 1][2];
            lazy = new int[maxSize + 1];
            size = new int[maxSize + 1];
            key = new long[maxSize + 1];
            cnt = new int[maxSize + 1];
            V = new int[maxSize + 1];
        }

        void pushUp(int x) {
            size[x] = ((size[children[x][0]] + size[children[x][1]]) % p + cnt[x]) % p;
            V[x] = (int)((V[children[x][0]] + V[children[x][1]] + key[x] * cnt[x] % p + p) % p);
        }

        void pushDown(int x) {
            if (lazy[x] != 0) {
                tag(children[x][0], lazy[x]);
                tag(children[x][1], lazy[x]);
                lazy[x] = 0;
            }
        }

        void tag(int x, long k) {
            if (x == 0) return;
            lazy[x] += k;
            key[x] += k;
            V[x] = (int)((V[x] + size[x] * k % p + p) % p);
        }

        void upRotate(int x) {
            int y = father[x], z = father[y], c = get(x);
            pushDown(y);
            pushDown(x);
            children[y][c] = children[x][c ^ 1];
            if (children[x][c ^ 1] != 0)
                father[children[x][c ^ 1]] = y;
            if (z != 0)
                children[z][get(y)] = x;
            children[x][c ^ 1] = y;
            father[y] = x;
            father[x] = z;
            pushUp(y);
            pushUp(x);
        }

        void splay(int x) {
            for (int f; (f = father[x]) != 0; upRotate(x))
                if (father[f] != 0) upRotate(get(x) == get(f) ? f : x);
            root = x;
        }

        void add(int x, int k) {
            if (root == 0) {
                key[++cur] = x;
                cnt[cur] = k;
                root = cur;
                pushUp(cur);
            } else {
                int cur = root, fa = 0;
                while (true) {
                    pushDown(cur);
                    if (key[cur] == x) {
                        cnt[cur] = (cnt[cur] + k) % p;
                        break;
                    }
                    fa = cur;
                    cur = children[cur][key[cur] >= x ? 0 : 1];
                    if (cur == 0) {
                        cur = ++this.cur;
                        key[cur] = x;
                        cnt[cur] = k;
                        father[cur] = fa;
                        children[fa][key[fa] >= x ? 0 : 1] = cur;
                        break;
                    }
                }
                pushUp(cur);
                pushUp(fa);
                splay(cur);
            }
        }

        void updateAll(int k) { tag(root, k); }

        void deleteFloor(int k) {
            add(k, 0);
            children[root][0] = 0;
            pushUp(root);
        }

        int deleteHigher(int k) {
            add(k, 0);
            int res = children[root][1];
            children[root][1] = 0;
            pushUp(root);
            return res;
        }

        void f(int x, int k) {
            if (x == 0) return;
            add(k, size[x]);
            add(1, (int)((V[x] - (long)size[x] * k % p + p) % p));
        }

        int get(int x) { return x == children[father[x]][0] ? 0 : 1; }

        int V() { return V[root]; }
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }

        long readLong() { return Long.parseLong(read()); }
    }
}

---

#H 和与乘积

时间限制: $1.0$s 内存限制: $512.0$MB 本题总分：$20$分

---

问题描述

  给定一个数列 $A=(a_1,a_2,\cdots ,a_n)$，问有多少个区间 $[L,R]$ 满足区间内元素的乘积等于他们的和，即 $a_L\cdot a_{L+1}\cdots \cdot a_R=a_L+a_{L+1}+\cdots +a_R$ 。

---

输入格式

  输入第一行包含一个整数 $n$，表示数列的长度。
  第二行包含 $n$ 个整数，依次表示数列中的数 $a_1,a_2,\cdots ,a_n$。

---

输出格式

  输出仅一行，包含一个整数表示满足如上条件的区间的个数。

---

测试样例₁

Input：
4
1 3 2 2

Output：
6

Explanation：
符合条件的区间为 [1, 1], [1, 3], [2, 2], [3, 3], [3, 4], [4, 4]。

---

评测用例规模与约定

  对于 $20$% 的评测用例，$n\le 3000$；
  对于 $50$% 的评测用例，$n\le 20000$；
  对于所有评测用例，$1\le n\le 200000,1\le ai\le 200000$。

---

前缀和

---

  强行打了个标题，其实不用前缀和做也行，

  虽然很难在累加对和和累乘对积中找到什么有用的共性，

  但我们显然可以知道，大于一的正整数累乘起来增长速度特别快，我们所熟知的 $2^{31}\simeq 2.1E9$ 就是 31 个一累乘，它的积大于二十一亿。

  如果我们当前累积的积大于 $n\cdot \mathrm{m}\mathrm{a}\mathrm{x}(\{a_i\})$，我们就可认为包含当前序列的其他序列都不可能出现和与乘积相等的情况，在给定的数据规模下，不超过三十六个任意大于二的正整数就可以超过这个界限。

  于是我们可以将一和其他正整数分开来处理(因为一对乘积没有贡献)，建立一个由大于一的正整数构成的子序列，在这个子序列中寻找原序列是否存在和与乘积相等的子序列，

  其复杂度接近线性，

  没啥好论的，很简单的题，别被我绕晕了。

import java.io.*;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        int n = in.readInt(), ans = n, N = 1, a;
        long[] A = new long[n + 1];
        long[] S = new long[n + 1];
        int[] O = new int[n + 2];
        for (int i = 0; i < n; i++) {
            a = in.readInt();
            if (a == 1) {
                S[N]++;
                O[N]++;
            } else {
                S[N] += S[N - 1] + a;
                A[N++] = a;
            }
        }
        long max = S[N - 1] + O[N];
        for (int i = 1; i < N; i++) {
            long pro = A[i];
            for (int j = i + 1; j < N; j++) {
                pro *= A[j];
                if (pro > max) break;
                long dif = pro - S[j] + S[i - 1] + O[i];
                if (dif == 0) ans++;
                else if (dif > 0 && O[i] + O[j + 1] >= dif) {
                    long l = Math.min(dif, O[i]);
                    long r = Math.min(dif, O[j + 1]);
                    ans += l + r - dif + 1;
                }
            }
        }
        System.out.println(ans);
    }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) { this.reader = new BufferedReader(new InputStreamReader(in)); }

        String read() {
            while (token == null || !token.hasMoreTokens())
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

---

#I 异或三角

时间限制: $5.0$s 内存限制: $512.0$MB 本题总分：$25$分

---

问题描述

  给定 $T$ 个数 $n_1,n_2,\cdot \cdot \cdot ,n_T$，对每个 $n_i$ 请求出有多少组 $a,b,c$ 满足：
  $1$. $1\le a,b,c\le n_i$；
  $2$. $a\oplus b\oplus c=0$，其中 $\oplus$ 表示二进制按位异或；
  $3$. 长度为 $a,b,c$ 的三条边能组成一个三角形。

---

输入格式

  输入的第一行包含一个整数 $T$。
  接下来 $T$ 行每行一个整数，分别表示 $n_1,n_2,\cdot \cdot \cdot ,n_T$。

---

输出格式

  输出 $T$ 行，每行包含一个整数，表示对应的答案。

---

测试样例₁

Input：
2
6
114514

Output：
6
11223848130

---

评测用例规模与约定

  对于 $10$% 的评测用例，$T=1,1\le n_i\le 200$；
  对于 $20$% 的评测用例，$T=1,1\le n_i\le 2000$；
  对于 $50$% 的评测用例，$T=1,1\le n_i\le 2^{20}$；
  对于 $60$% 的评测用例，$1\le T\le 100000,1\le n_i\le 2^{20}$；
  对于所有评测用例，$1\le T\le 100000,1\le n_i\le 2^{30}$。

---

  ?这数据

---

线性递推

---

  都线性了，那 $40$% 的 $2^{30}$ 就不用想了。

  先是要确定几个能帮助我们加快程序运行速度的性质。

  $a\oplus a=0$，$0\oplus 0=0$，因此 $a,b,c$ 互不相等，对于最终计算出的方案数，我们只需在计算时满足 $a>b>c$，然后对结果乘以 $3!$。

  而 $a<b+c$ 才能组成三角形，故需要满足 $a=b\oplus c<b+c$。

  我们都知道异或还有个别名，模二意义下的加法，也就是两个数做异或运算相当在二进制下做加法并舍弃进位。

  因此当 $b$ 与 $c$ 有任意一位同为 $1$ 时，加法运算发生进位，不等式成立。

  再考虑对任意 $a$ 可能的方案数，

  $a\ge 1$，因此 $a$ 能被表示为 $1x_1{x}_2\cdots x_m$ 这种 $1$ 接后继二进制串的形式；为了使 $a>b>c$，$b$、$c$ 的二进制表示长度不会大于 $a$；为了使 $a=b\oplus c$，$b$ 也必须被表现为 $1y_1{y}_2\cdots y_m$ 这种形式；

  因此 $b$ 绝对大于 $c$，所以我们可以直接跳过对 $c$ 的讨论。

  受上述条件限制，$c$ 有和 $b$ 相同位 $1$ 的充分条件是 $a$ 在此位为 $0$，所以 $b$ 在小于 $a$ 的同时，必须还有一位二进制数与 $a$ 相反，为了满足这个性质，这里换一种思路。

  直接选择所有 $1y_1{y}_2\cdots y_m$，$y_1{y}_2\cdots y_m<x_1{x}_2\cdots x_m$，然后从中剔除不满足性质的元素。

  选择这个集合等价于增加 $a$ 去掉前导 $1$ 的一串二进制数，而去掉不满足性质的元素，等价于减去 $2$ 的这串二进制数中 $1$ 的个数次幂。

  举个例子：

  设 $a$ 为 $0\mathrm{b}101011$，$b$ 必大于 $0\mathrm{b}100000$，因此我们直接选中 $[0\mathrm{b}100000,0\mathrm{b}101011)$ 即 $0\mathrm{b}101011-0\mathrm{b}100000=0\mathrm{b}1011$ 个元素，而不存在 $a$ 该位为 $0$ 而 $b$ 不为 $1$ 这种情况的集合为 $\{0\mathrm{b}{x}_{1}0x_2{x}_3\}$，$x_i\in 0or1$，显然集合元素数量为 $2^{\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\mathrm{B}\mathrm{i}\mathrm{t}(0\mathrm{b}1011)}$，相减后即为我们想要的结果。

---

import java.io.*;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    void run() {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out);
        int T = in.readInt(), upper = 0;
        int[] Q = new int[T];
        for (int i = 0; i < T; i++)
            upper = max(upper, Q[i] = in.readInt());
        long[] A = new long[upper + 1];
        for (int i = 1; i <= upper; i++) {
            int b = i - highBit(i);
            A[i] = A[i - 1] + b - (1 << countBit(b)) + 1;
        }
        for (int i = 0; i < T; i++)
            out.println(6 * A[Q[i]]);
        out.flush();
    }

    int highBit(int n) {
        n |= (n >> 1);
        n |= (n >> 2);
        n |= (n >> 4);
        n |= (n >> 8);
        n |= (n >> 16);
        return n - (n >>> 1);
    }

    int countBit(int n) {
        n = n - ((n >>> 1) & 0x55555555);
        n = (n & 0x33333333) + ((n >>> 2) & 0x33333333);
        n = (n + (n >>> 4)) & 0x0f0f0f0f;
        n += n >>> 8;
        n += n >>> 16;
        return n & 0x3f;
    }

    int max(int a, int b) { return a > b ? a : b; }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

---

组合数学

---

  根据上述递推，显然有对于每个询问 $n_i$，都有回答

  $\sum _{i=1}^{n_j}(j+1-highBit(j)-2^{countBit(j)-1})$，即

  $\frac{n_i(n_i+3)}{2}-\sum _{j=1}^{n_i}(highBit(j)+2^{countBit(j)-1})$

  对于每个 $\sum _{j=1}^{n_i}highBit(j)$，都可以分解为

  $\sum _{k=1}^{\lfloor {\log }_2{n}_i\rfloor }\sum _{j=2^{k-1}}^{2^k-1}highBit(j)+(n_i-n_i^{\lfloor {\log }_2{n}_i\rfloor }+1)highBit(n_i^{\lfloor {\log }_2{n}_i\rfloor })$

  这个式子过于简单，这里便不再讨论，

  重点在 $\sum _{j=1}^{n_i}{2}^{countBit(j)-1}=\frac{\sum _{j=1}^{n_i}{2}^{countBit(j)}}{2}$ 部分，为了方便讨论，这只讨论分子部分并变换符号，

  于是有公式 $\sum _{i=1}^n{2}^{countBit(i)}$

  $=\sum _{i=1}^{2^k}{2}^{countBit(i)}+\sum _{i=1}^{n-2^k}{2}^{countBit(i+2^k)}$，其中 $k=\lfloor {\log }_2{n}_i\rfloor$。

  显然第二项中，每个 $i$ 都不大于 $2^k$，在 $countBit$ 意义下，$countBit(i+2^k)=countBit(i)+1$。

  因此，$\sum _{i=1}^n{2}^{countBit(i)}=\sum _{i=1}^{2^k}{2}^{countBit(i)}+2\times \sum _{i=1}^{n-2^k}{2}^{countBit(i)}$。

  而对于 $n=2^k$，$k\in N$ 的情况，我们可以对 $[1,2^{k-1}]$ 做仿射变换到 $[1,2^k]$，同时映射出结果。

  更详细的说，

  定义正整数数集 $N_k\in [1,2^k]$，常量 $A_k=\sum _{i=1}^{N^k}{2}^{countBit(i)}$。

  $N_0=\{1\}$，$N_{k+1}$ 中的元素由 $N_k$ 做 $k=2$，$b=\{0,1\}$ 的两次仿射变换而来，特殊的，$2^k$ 映射为 $1$。

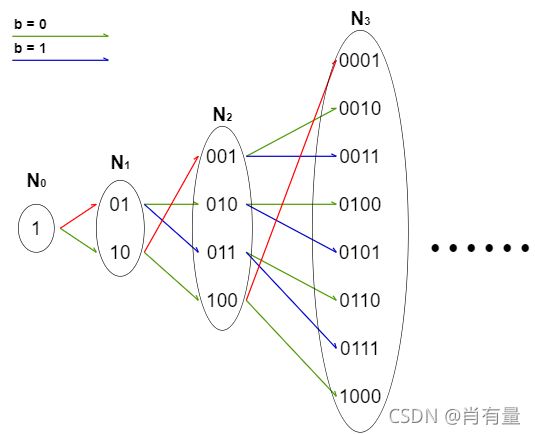
  $N^k$ 中没有重复元素，同时仿射变换 $b=\{0,1\}$ 的两种情况的奇偶性是不相同的，因此映射得到的 $N^{k+1}$ 集合是完全的。

  $2N^k+0$ 显然等于 $A_k$，而 $2N^k+1$ 时，每次特殊映射的 $2^k$ bit 数为 $1$，$2^k$ 映射为 $1$ 后 bit 数同为 $1$，因此 $2N^k+1=2(A_k-1)+1$。

  整理可得$$A_k=3A_{k-1}-1=\sum _{i=1}^{2^k}{2}^{countBit(i)}=\{\begin{array}{lr}1& k=0\\ 3\sum _{i=1}^{2^{k-1}}{2}^{countBit(i)}-1& \end{array}$$

  至此，我们整理出一套可以在 $O(\log n_i)$ 内计算出 $\sum _{i=1}^{n_i}(i+1-highBit(i)-2^{countBit(i)-1})$ 的公式。

---

import java.io.*;
import java.util.StringTokenizer;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    long[] highB = new long[0x20];
    long[] countB = new long[0x20];

    void run() {
        InputReader in = new InputReader(System.in);
        PrintWriter out = new PrintWriter(System.out);
        int T = in.readInt(), n, m, k;
        countB[0] = 1;
        for (int i = 1; i < 0x20; i++) {
            highB[i] = (highB[i - 1] << 2) | 1;
            countB[i] = countB[i - 1] * 3 - 1;
        }
        while (T-- > 0) {
            n = in.readInt();
            k = floorLog2(n);
            m = n - (1 << k);
            out.println(6 * (
                (n + 3L) * n / 2 -
                (calcCountBit(n)) -
                highB[k] - (m + 1L) * (1 << k)
            ));
        }
        out.flush();
    }

    long calcCountBit(int n) {
        if (n == 0) return 0;
        int m = highBit(n);
        long ans = countB[floorLog2(m)];
        if (n != m)
            ans += calcCountBit(n - m) << 1;
        return ans;
    }

    int[] FLOOR_LOG2_TABLE = { 0, 0, 1, 26, 2, 23, 27, 32, 3, 16, 24, 30, 28, 11, 33, 13, 4, 7, 17, 35, 25, 22, 31, 15, 29, 10, 12, 6, 34, 21, 14, 9, 5, 20, 8, 19, 18 };

    int highBit(int n) {
        n |= (n >> 1);
        n |= (n >> 2);
        n |= (n >> 4);
        n |= (n >> 8);
        n |= (n >> 16);
        return n - (n >>> 1);
    }

    int floorLog2(int a) { return FLOOR_LOG2_TABLE[highBit(a) % 37]; }

    class InputReader {

        BufferedReader reader;
        StringTokenizer token;

        InputReader(InputStream in) {
            this.reader = new BufferedReader(new InputStreamReader(in));
        }

        String read() {
            while (token == null || !token.hasMoreTokens()) {
                try {
                    token = new StringTokenizer(reader.readLine());
                } catch (IOException e) {
                    e.printStackTrace();
                }
            }
            return token.nextToken();
        }

        int readInt() { return Integer.parseInt(read()); }
    }
}

---

#J 积木

时间限制: $10.0$s 内存限制: $512.0$MB 本题总分：$25$分

---

问题描述

  小蓝有大量正方体的积木（所有积木完全相同），他准备用积木搭一个巨大的图形。
  小蓝将积木全部平铺在地面上，而不垒起来，以便更稳定。他将积木摆成一行一行的，每行的左边对齐，形成最终的图形。
  第一行小蓝摆了 $H_1=w$ 块积木。从第二行开始，第 $i$ 行的积木数量 $H_i$ 都至少比上一行多 $L$，至多比上一行多 $R$（当 $L=0$ 时表示可以和上一行的积木数量相同），即 $H_{i-1}+L\le H_i\le H_{i-1}+R$。
  给定 $x,y$ 和 $z$，请问满足以上条件的方案中，有多少种方案满足第 $y$ 行的积木数量恰好为第 $x$ 行的积木数量的 $z$ 倍。

---

输入格式

  输入一行包含 $7$ 个整数 $n,w,L,R,x,y,z$，意义如上所述。

---

输出格式

  输出一个整数, 表示满足条件的方案数，答案可能很大，请输出答案除以 $998244353$ 的余数。

---

测试样例₁

Input：
5 1 1 2 2 5 3

Output：
4

样例说明₁

符合条件的积木如图所示

测试样例₂

Input：
233 5 1 8 100 215 3

Output：
308810105

---

评测用例规模与约定

  对于 $10$% 的评测用例，$1\le n\le 10,1\le w\le 10,0\le L\le R\le 3$；
  对于 $20$% 的评测用例，$1\le n\le 20,1\le w\le 10,0\le L\le R\le 4$；
  对于 $35$% 的评测用例，$1\le n\le 500,0\le L\le R\le 10$；
  对于 $50$% 的评测用例，$1\le n\le 5000,0\le L\le R\le 10$；
  对于 $60$% 的评测用例，$1\le n\le 20000,0\le L\le R\le 10$；
  对于 $70$% 的评测用例，$1\le n\le 50000,0\le L\le R\le 10$；
  对于 $85$% 的评测用例，$1\le n\le 300000,0\le L\le R\le 10$；
  对于所有评测用例，$1\le n\le 500000,1\le w\le 10^9,0\le L\le R\le 40,1\le x<y\le n,0\le z\le 10^9$。

---

泰勒展开

---

  符号太乱了，重新整理一下。

---

前置知识

---

独立随机变量和分布 & 卷积

  如果想知道若干个不同的正整数 $a_1,a_2,\cdots a_k$，从中任取 $n$ 次，每次取一个数，组成一个正整数 $A$ 能有多少种组法，一个方法使设函数 $f(x)=x^{a_1}+x^{a_2}+\cdots +x^{a_k}$，它的 $n$ 次卷积在 $x^A$ 项上的系数即是要求出方案数。

  举例来说，我们有 $0,1$，于是 $f(x)=1+x$。

  $f^2(x)=1+2x+x^2$

  $f^3(x)=1+3x+3x^2+x^3$

  $...$

  对应的，若想知道从 $\{0,1\}$ 中取 $3$ 个数组成 $2$ 一共有多少种取法，只需求出 $[x^2]f^3(x)=3$ 即可，其中 $[x^i]f(x)$ 表示取出多项式 $f(x)$ 在 $x^i$ 项上的系数。

  而这个过程可以被称为独立随机变量和的卷积，

  学有余力的读者可以自行了解。

---

泰勒展开式

  如果一个函数 $f(x)$ 在 $x_0$ 处的 $1$ 至 $n+1$ 阶导数都存在，是否能找到一个多项式 $P_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0{)}^2+\cdots +a_n(x-x_0{)}^n$ 使得，

  $f(x)\simeq P_n(x)$，

  答案是肯定的，只需令 $P_n(x)=\sum _{k=0}^n\frac{f^{(k)}(x_0)}{k!}(x-x_0{)}^k$

  如果$f(x)$也是多项式，这时我们就能引入 $[x^i]f(x)=\frac{f^{(i)}(0)}{i!}$，

  事实上不用泰勒也可能得到这个结论，

  学有余力的读者可以自行证明。

---

莱布尼茨公式

  两个函数乘积的高阶导数可以表示为，

  $(uv{)}^{(n)}=\sum _{k=0}^n{C}_n^k{u}^{(n-k)}{v}^{(k)}$

  引入一下方便计算。

---

  回到原问题，

  如果对函数 $f(\alpha )=({\alpha }^L+{\alpha }^{L+1}+\cdots +{\alpha }^R)$，分别求出 $f^x(\alpha )$、$f^{y-x}(\alpha )$，那答案即为 ${\sum }_{k=0}([x^k]f^x(\alpha )[x^{zk}]f^{y-x}(\alpha ))$，只要能对任意 $L$、$R$、$x$、$y$ 快速求出卷积或高阶导，问题就迎刃而解，但朴素求高阶导数复杂度过高，$5\times 40\times 1e5\ge 2^{24}$，$\mathrm{F}\mathrm{F}\mathrm{T}$ 过大的常数难于驾驭，而题目给出的模数 $998244353=7\times 17\times 2^{23}$，因此也无法选择 $\mathrm{N}\mathrm{T}\mathrm{T}$。

  于是考虑对高阶求导化简，

  为了方便讨论，设函数

  $\begin{array}{rl}f(x)& =x^0+x^1+\cdots +x^{K-1}=\frac{1-x^K}{1-x}\\ f^N(x)& ={\left(\frac{1-x^K}{1-x}\right)}^N=(1-x^K{)}^N(1-x{)}^{-N}\end{array}$

  解决了对于任意 $N$、$K$ 的快速求高阶导，就等价于解决了上述问题。

  $v(x)=(1-x{)}^{-N}$ 的高阶导 $v^{(n)}(0)=\frac{(N-1+n)!}{(N-1)!}$

  $v$ 倒是好求，那 $u(x)=(1-x^K{)}^N$ 呢。

  但其实可以把 $u$ 按二项式展开，

  $u(x)=\sum _{k=0}^n{C}_n^k(-x^K{)}^k{y}^{n-k}$，$u^{(n)}(0)=\{\begin{array}{rl}(-1{)}^k{C}_N^{\frac{k}{K}}k!& k\mid K\\ 0& k\nmid K\end{array}$

  结合莱布尼茨公式有，

  $\begin{array}{rl}{f}^{N(n)}(0)& =\frac{1}{(N-1)!}\sum _{k=0,k\mid K}^n(-1{)}^k{C}_n^k{C}_N^{\frac{k}{K}}k!(N+n-k-1)!\\ [x^n]f^N& =\frac{1}{(N-1)!n!}\sum _{k=0,k\mid K}^n(-1{)}^k{C}_N^{\frac{k}{K}}\frac{n!k!(N+n-k-1)!(N-1)!}{k!(n-k)!(N-1)!}\\ [x^n]f^N& =\sum _{k=0,k\mid K}^n(-1{)}^k{C}_N^{\frac{k}{K}}{C}_{N+n-k-1}^{N-1}\end{array}$

  好像将死了，
  

---

骗分

---

  肝了一下

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.StreamTokenizer;
import java.io.IOException;

public class Main {

    public static void main(String[] args) { new Main().run(); }

    int p = 998244353;

    int[] swap;

    void run() {
        int n = nextInt(), w = nextInt(), L = nextInt(), R = nextInt(), x = nextInt(), y = nextInt(), z = nextInt();
        int lim = limit(Math.max(x - 1, y - x) * (R - L) + 1), ans = 0;
        swap = new int[lim];
        int[] A = new int[lim];
        int[] B = new int[lim];
        for (int i = 0; i < lim; i++)
            swap[i] = (i & 1) * (lim >> 1) | (swap[i >> 1] >> 1);
        for (int i = 0; i <= R - L; i++) A[i] = 1;
        NTT(A, lim, 1);
        for (int i = 0; i < lim; i++) {
            B[i] = qpow(A[i], y - x);
            A[i] = qpow(A[i], x - 1);
        }
        NTT(A, lim, -1);
        NTT(B, lim, -1);
        for (int i = 0; i <= (x - 1) * (R - L); i++) {
            int tmp = z * (w + (x - 1) * L + i) - w - i - (y - 1) * L;
            if (tmp >= lim) break;
            ans = (int)((ans + (long)A[i] * B[tmp]) % p);
        }
        System.out.println((long)ans * qpow(R - L + 1, n - y) % p);
    }

    int qpow(long a, int n) {
        long res = 1;
        while (n > 0) {
            if ((n & 1) == 1) res = res * a % p;
            a = a * a % p;
            n >>= 1;
        }
        return (int)res;
    }

    void NTT(int[] F, int lim, int opt) {
        for (int i = 0; i < lim; i++) {
            if (swap[i] < i) {
                int t = F[i];
                F[i] = F[swap[i]];
                F[swap[i]] = t;
            }
        }
        for (int len = 2; len <= lim; len <<= 1) {
            long gn = qpow(3, (p - 1) / len);
            int k = len >> 1;
            for (int i = 0; i < lim; i += len) {
                long g = 1, tmp;
                for (int j = 0; j < k; j++, g = g * gn % p) {
                    tmp = F[i + j + k] * g % p;
                    F[i + j + k] = (int)((F[i + j] - tmp + p) % p);
                    F[i + j] = (int)((F[i + j] + tmp) % p);
                }
            }
        }
        if (opt == -1) {
            for (int i = 1, j = lim - 1; i < j; i++, j--) {
                int t = F[i];
                F[i] = F[j];
                F[j] = t;
            }
            long inv = qpow(lim, p - 2);
            for (int i = 0; i < lim; i++) F[i] = (int)(F[i] * inv % p);
        }
    }

    StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));

    int limit(int lim) { return Integer.highestOneBit(lim) == lim ? lim : (Integer.highestOneBit(lim) << 1); }

    int nextInt() {
        try {
            in.nextToken();
        } catch (IOException e) {
            e.printStackTrace();
        }
        return (int)in.nval;
    }
}

  $85$% 的用例就 $85$ 吧。