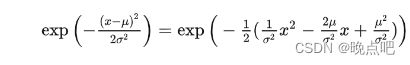Diffusion mdoel: Denoising Diffusion Probabilistic Models论文解读及实现(一)
论文地址:https://arxiv.org/pdf/2006.11239.pdf
1 正向加噪推导
**核心公式1 **
x t = α ˉ t ∗ x 0 + 1 − α ˉ t z t x_t=\sqrt{\bar \alpha_t}*x_{0}+\sqrt{1-\bar \alpha_t}z_t xt=αˉt∗x0+1−αˉtzt
证明如下:
α t = 1 − β t β 越来越大,则 α 越来越小 \alpha _t=1-\beta_t \quad\beta越来越大,则\alpha越来越小 αt=1−βtβ越来越大,则α越来越小
x t 和 x t − 1 的关系: x t = α t ∗ x t − 1 + 1 − α t z 1 x_t和x_{t-1} 的关系: \quad x_t=\sqrt{\alpha_t}*x_{t-1} + \sqrt{1-\alpha_t}z_1 xt和xt−1的关系:xt=αt∗xt−1+1−αtz1
x t − 1 和 x t − 2 的关系: x t − 1 = α t − 1 ∗ x t − 2 + 1 − α t z 2 x_{t-1}和x_{t-2} 的关系: \quad x_{t-1}=\sqrt{\alpha_{t-1}}*x_{t-2} + \sqrt{1-\alpha_t}z_2 xt−1和xt−2的关系:xt−1=αt−1∗xt−2+1−αtz2
上式进行合并: x t = α t ∗ ( α t − 1 ∗ x t − 2 + 1 − α t z 2 ) + 1 − α t z 1 上式进行合并:\quad x_t=\sqrt{\alpha_t}*(\sqrt{\alpha_{t-1}}*x_{t-2} + \sqrt{1-\alpha_t}z_2 ) + \sqrt{1-\alpha_t}z_1 上式进行合并:xt=αt∗(αt−1∗xt−2+1−αtz2)+1−αtz1
由于每次加入的噪声都是服从高斯分布的
x t = α t ∗ α t − 1 ∗ x t − 2 + α t 1 − α t − 1 z 2 + 1 − α t z 1 x_t=\sqrt{\alpha_t}*\sqrt{\alpha_{t-1}}*x_{t-2} +\sqrt{\alpha_t} \sqrt{1-\alpha_{t-1}}z_2 + \sqrt{1-\alpha_t}z_1 xt=αt∗αt−1∗xt−2+αt1−αt−1z2+1−αtz1
z 1 服从 N ( 0 , 1 − α t ) z 2 服从 N ( 0 , α t ( 1 − α t − 1 ) ) z_1 服从 N(0,1-\alpha_t) \\ z_2服从 N(0,\alpha_t(1-\alpha_{t-1})) z1服从N(0,1−αt)z2服从N(0,αt(1−αt−1))
根据高斯分布公式合并x_t的噪声项,
N ( 0 , σ 1 2 I ) + N ( 0 , σ 2 2 I ) − N ( 0 , ( σ 1 2 + σ 2 2 ) I ) N(0,\sigma_1^2I) + N(0,\sigma_2^2I) - N(0,(\sigma_1^2+\sigma_2^2)I) ~~ N(0,σ12I)+N(0,σ22I)−N(0,(σ12+σ22)I)
基于上式高斯混合分布公式可简化x_t
x t = α t α t − 1 ∗ x t − 2 + 1 − α t ∗ α t − 1 z x_t=\sqrt{\alpha_t\alpha_{t-1}}*x_{t-2} +\sqrt{1-\alpha_t*\alpha_{t-1}}z xt=αtαt−1∗xt−2+1−αt∗αt−1z
由上可递推
x t = α t α t − 1 . . . α 0 ∗ x 0 + 1 − α t ∗ α t − 1 . . . α 0 z t 令 α t ∗ α t − 1 . . . α 0 = α ˉ t x t = α ˉ t ∗ x 0 + 1 − α ˉ t z t x_t=\sqrt{\alpha_t\alpha_{t-1}...\alpha_0}*x_{0} +\sqrt{1-\alpha_t*\alpha_{t-1}...\alpha_0}z_t \\ 令\alpha_t*\alpha_{t-1}...\alpha_0=\bar \alpha_t \\ x_t=\sqrt{\bar \alpha_t}*x_{0}+\sqrt{1-\bar \alpha_t}z_t xt=αtαt−1...α0∗x0+1−αt∗αt−1...α0zt令αt∗αt−1...α0=αˉtxt=αˉt∗x0+1−αˉtzt
有了上述公式,在已知x_0时,任意时刻的x_t都可以计算得出。
2 反向去噪推导
去噪需要求解的是在给定x_0,x_t时,求解x_{t-1}时刻概率
q ( x t − 1 ∣ x t , x 0 ) q(x_{t-1}|x_t,x_0) q(xt−1∣xt,x0)
根据贝叶斯公式
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) q(x_{t-1}|x_t,x_0)=q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_{t}|x_0)} q(xt−1∣xt,x0)=q(xt∣xt−1,x0)q(xt∣x0)q(xt−1∣x0)
根据上面第一节中的正向加噪公式
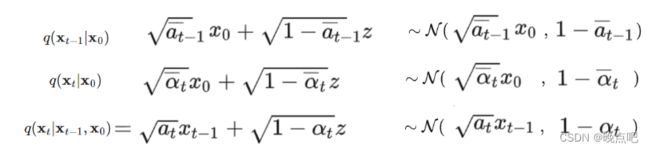
则:
q ( x t − 1 ∣ x t , x 0 ) = e x p ( − 1 2 ( ( x t − 1 − α ˉ t − 1 x 0 ) 2 1 − α ˉ t − 1 + ( x t − α t x t − 1 ) 2 1 − α t − ( x t − α ˉ t x 0 ) 2 1 − α ˉ t ) ) q(x_{t-1}|x_t,x_0)= exp(-\frac{1}{2} (\frac{(x_{t-1}-\sqrt{\bar \alpha_{t-1}}x_0)^2}{1-\bar \alpha_{t-1}} + \frac{(x_{t}-\sqrt{\alpha_{t}}x_{t-1})^2}{1- \alpha_{t}} - \frac{(x_{t}-\sqrt{\bar \alpha_{t}}x_0)^2}{1-\bar \alpha_{t}}) ) q(xt−1∣xt,x0)=exp(−21(1−αˉt−1(xt−1−αˉt−1x0)2+1−αt(xt−αtxt−1)2−1−αˉt(xt−αˉtx0)2))
将上式进行化简:
e x p ( − 1 2 ( α t 1 − α t + 1 1 − α ˉ t − 1 ) x t − 1 2 − ( 2 α t 1 − α t x t + 2 α ˉ t − 1 1 − α ˉ t − 1 x 0 ) x t − 1 + C ( x t , x 0 ) ) exp(-\frac{1}{2} (\frac{\alpha_t}{1-\alpha_t}+\frac{1}{1-\bar \alpha_{t-1}})x_{t-1}^2 - (\frac{2\sqrt{\alpha_{t}} } {1- \alpha_{t}} x_t +\frac{2\sqrt{\bar \alpha_{t-1}}}{1-\bar \alpha_{t-1}}x_0)x_{t-1} + C (x_t,x_0)) exp(−21(1−αtαt+1−αˉt−11)xt−12−(1−αt2αtxt+1−αˉt−12αˉt−1x0)xt−1+C(xt,x0))
根据下面高斯展开式,二次方与二次方对齐,一次方与一次方对齐,配平上式,可求均值和方差
μ ˉ t ( x t , x 0 ) = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t x t + α ˉ t − 1 ( 1 − α t ) 1 − α ˉ t x 0 \bar \mu_t(x_t,x_0)=\frac{\sqrt{\alpha_{t}}(1-\bar \alpha_{t-1} ) } {1- \bar \alpha_{t}} x_t +\frac{\sqrt{\bar \alpha_{t-1}}(1-\alpha_t) } {1- \bar \alpha_{t}} x_0 μˉt(xt,x0)=1−αˉtαt(1−αˉt−1)xt+1−αˉtαˉt−1(1−αt)x0
上式中含有x_0,由于x_0是未知的,根据正向公式
x t = α ˉ t ∗ x 0 + 1 − α ˉ t z t x_t=\sqrt{\bar \alpha_t}*x_{0}+\sqrt{1-\bar \alpha_t}z_t xt=αˉt∗x0+1−αˉtzt
x 0 = ( x t − 1 − α ˉ t z t ) α ˉ t x_{0}=\frac{(x_t-\sqrt{1-\bar \alpha_t}z_t)}{\sqrt{\bar \alpha_t}} x0=αˉt(xt−1−αˉtzt)
可得最终 均值
核心公式2
μ ˉ t = 1 α t ( x t − 1 − α t 1 − α ˉ t z t ) \bar \mu_t=\frac{1 } {\sqrt \alpha_{t}} (x_t -\frac{1-\alpha_t } {\sqrt{1- \bar \alpha_{t}}} z_t) μˉt=αt1(xt−1−αˉt1−αtzt)
上式中z_t是通过网络学习出来的
3 diffusion模型算法
1)训练
核心公式1
x t = α ˉ t ∗ x 0 + 1 − α ˉ t z t x_t=\sqrt{\bar \alpha_t}*x_{0}+\sqrt{1-\bar \alpha_t}z_t xt=αˉt∗x0+1−αˉtzt

2)采样
核心公式2
μ ˉ t = 1 α t ( x t − 1 − α t 1 − α ˉ t z t ) \bar \mu_t=\frac{1 } {\sqrt \alpha_{t}} (x_t -\frac{1-\alpha_t } {\sqrt{1- \bar \alpha_{t}}} z_t) μˉt=αt1(xt−1−αˉt1−αtzt)