【StyleGAN2论文精读CVPR_2020】Analyzing and Improving the Image Quality of StyleGAN

一、前言

【Paper】 > 官方TensorFlow版【Code】 > Pytorch版【Code】> 【Project】
本篇博客是StyleGAN2论文的中文精读，望于大家全面理解StyleGAN2生成器有一定的帮助。
Pipeline：

1. 首先，由于AdaIN操作会产生水滴状伪影，解决方案是重新设计normalization归一化步骤。详细见图2。
2. 修改包括Weight demodulation， Lazy regularization， Path length regularization， No growing, new G & D arch， Large networks (StyleGAN2)。

Abstract

背景：基于样式的GAN体系结构(StyleGAN)在数据驱动的无条件生成图像建模中产生了最先进的结果。
方法：我们公开并分析它的几个特征伪影，并在模型架构和训练方法中提出改变来解决它们。
特别是，我们重新设计了生成器的归一化，重新访问了渐进增长，并正则化了生成器，以鼓励从潜码到图像的映射中良好的调节。
除了改善图像质量，这个路径长度正则化器还产生了额外的好处，即生成器变得更容易反演。
这使得可靠地将生成的图像归为特定的网络成为可能。
我们进一步将生成器如何很好地利用其输出分辨率可视化，并识别容量问题，激励我们训练更大的模型以获得额外的质量改进。
总结：总的来说，我们的改进模型重新定义了无条件图像建模的技术水平，包括现有的分布质量指标和感知图像质量。

1. Introduction

生成方法，特别是生成对抗网络(generative adversarial networks, GAN)[13]生成图像的分辨率和质量正在迅速提高[20,26,4]。
目前最先进的高分辨率图像合成方法是StyleGAN[21]，它已经被证明可以在各种数据集上可靠地工作。
我们的工作集中在修复其特征伪影和进一步提高结果质量。

StyleGAN {Karras2018} 的显着特征是其非常规的生成器架构。
mapping network $f$ 不是仅将输入潜在代码 $\mathrm{z}\in \mathcal{Z}$ 馈送到网络的开头，而是首先将其转换为中间潜在代码 $\mathrm{w}\in \mathcal{W}$。
然后仿射变换产生 styles，通过自适应实例归一化 (AdaIN) {Huang2017,Dumoulin2016,Ghiasi2017,Dumoulin2018} 控制 synthesis network $g$ 的各层。
此外，通过向合成网络提供额外的随机噪声图来促进随机变化。
已经证明 {Karras2018,Shen2019}这种设计允许中间潜在空间 $\mathcal{W}$ 比输入潜在空间 $\mathcal{Z}$ 的纠缠少得多。
在本文中，我们将所有分析仅集中在 $\mathcal{W}$ 上，因为从合成网络的角度来看，它是相关的潜在空间。

许多观察者注意到 StyleGAN {Bergstrom2019} 生成​​的图像中存在特征伪影。
我们确定了这些伪影的两个原因，并描述了消除这些伪影的架构和训练方法的变化。
首先，我们调查了常见的斑点状伪影的起源，并发现生成器创建它们是为了规避其架构中的设计缺陷。
在Section 2中，我们重新设计了生成器中使用的标准化，从而消除了伪影。
其次，我们分析了与渐进式增长 {Karras2017} 相关的伪影，该伪影在稳定高分辨率 GAN 训练方面非常成功。
我们提出了一种实现相同目标的替代设计-------训练从关注低分辨率图像开始，然后逐渐将焦点转移到越来越高分辨率------而不在训练期间改变网络拓扑。
这种新设计还使我们能够推断生成图像的有效分辨率，结果证明该分辨率低于预期，从而激发了容量增加（Section 4）。

使用生成方法生成的图像质量的定量分析仍然是一个具有挑战性的话题。
$Fr\acute{e}chet$ 初始距离 (FID) {Heusel2017} 测量 InceptionV3 分类器 {simonyan2014} 的高维特征空间中两个分布的密度差异。
精确率和召回率 ($P\&R$) {Sajjadi2018,Tuomas2019} 通过分别显式量化与训练数据相似的生成图像的百分比和可以生成的训练数据的百分比来提供额外的可见性。
我们使用这些指标来量化改进。

FID 和 $P\&R$ 都基于最近被证明专注于纹理而不是形状的分类器网络{Geirhos2018}，因此，这些指标无法准确捕获图像质量的所有方面。
我们观察到，感知路径长度perceptual path length（PPL）度量{Karras2018}最初是作为估计潜在空间插值质量的方法引入的，它与形状的一致性和稳定性相关。
在此基础上，我们对合成网络进行正则化以有利于平滑映射（Section 3）并实现质量的明显提高。
为了抵消其计算成本，我们还建议减少执行所有正则化的频率，观察到这可以在不影响有效性的情况下完成。

最后，我们发现使用新的路径长度正则化 StyleGAN2 生成器将图像投影到潜在空间 $\mathcal{W}$ 的效果明显优于原始 StyleGAN。
这使得更容易将生成的图像归因于其源（Section 5）。

我们的实施和训练模型可在https://github.com/NVlabs/stylegan2获取。

2. Removing normalization artifacts

我们首先观察到，由StyleGAN生成的大多数图像都呈现出类似水滴的典型的斑点状伪影。
如图1所示，即使液滴在最终图像中可能不明显，但在generator¹的中间特征图中仍然存在。
这种异常开始出现在64×64分辨率附近，出现在所有的特征图中，并在更高分辨率时逐渐增强。
这种一致性伪影的存在是令人困惑的，因为鉴别器应该能够检测到它。

我们将问题定位到AdaIN操作中，该操作将每个特征图的均值和方差分别归一化，从而可能破坏在这些特征的相对大小中发现的任何信息。
我们假设，液滴伪迹是生成器有意在实例归一化之后偷偷获取信号强度信息的结果:通过创建一个强大的、局部的、占主导地位的峰值，生成器可以在其他地方有效地缩放信号。
我们的假设得到如下发现的支持:当归一化步骤从生成器中移除时，水滴伪影完全消失。

2.1. Generator architecture revisited

我们重新设计了 StyleGAN 合成网络的架构。
(a) 原始 StyleGAN，其中$\boxed{A}$ 表示从 $\mathcal{W}$ 学习的仿射变换，产生样式，而 $\boxed{B}$ 是噪声广播操作。
(b) 具有完整细节的同一张图。在这里，我们将 AdaIN 分解为显式归一化，然后进行调制，两者都对每个特征图的平均值和标准差进行操作。我们还注释了学习权重 ($w$)、偏差 ($b$)和常量输入 ($c$)，并重新绘制灰色框，以便每个框激活一种样式。激活函数（leaky ReLU）始终在添加偏差后立即应用。
( c) 我们对原始架构进行了一些修改，这些修改在正文中是合理的。我们在开始时删除了一些冗余操作，将 $b$ 和 $\boxed{B}$ 的添加移动到样式的活动区域之外，并仅调整每个特征图的标准偏差。
(d) 修改后的架构使我们能够用“解调”操作替换实例归一化，我们将其应用于与每个卷积层相关的权重。

我们将首先修改StyleGAN生成器的几个细节，以更好地促进我们重新设计的规范化。
就质量度量而言，这些变化本身具有中性或微小的积极影响。

图2a显示了原始的StyleGAN合成网络 $g$[21]，在图2b中，我们通过显示权重和偏差，并将AdaIN操作分解为两个组成部分:归一化和调制，将图展开到完整的细节。
这允许我们重新绘制概念上的灰色框gray boxes，以便每个灰色框表示网络中某个样式处于活动状态的部分(即“style block”)。
有趣的是，最初的StyleGAN在样式块中应用了bias和噪音，导致它们的相对影响与当前样式的大小成反比。
我们观察到，通过将这些操作移到样式块之外，可以获得更可预测的结果，在样式块中，它们对规范化数据进行操作。
此外，我们注意到，在这一变化之后，标准化和调制仅作用于标准差就足够了(即，不需要均值)。
对常数输入的偏置、噪声和归一化的应用也可以安全地删除，而没有明显的缺陷。
这个变体如图2c所示，它是我们重新设计的规范化的起点。

2.2. Instance normalization revisited

StyleGAN的主要优势之一是能够通过样式混合来控制生成的图像，也就是说，在推理时向不同的层输入不同的潜在w。
在实践中，样式调制可以将某些特征图放大一个数量级或更多。
为了使样式混合工作，我们必须明确地在每个样本的基础上抵消这种放大——否则后续的层将无法以有意义的方式对数据进行操作。

如果我们愿意牺牲特定规模的控制(见视频)，我们可以简单地删除标准化，从而删除伪影，并略微改进FID[22]。
现在我们将提出一个更好的替代方案，在保留完全可控性的同时删除伪影。
其主要思想是将规范化建立在传入特性映射的预期统计数据的基础上，但没有明确的强制要求。

回想一下，图2c中的样式块由调制、卷积和归一化组成。
让我们从考虑调制后的卷积的影响开始。
调制根据传入的样式对卷积的每个输入特征图进行缩放，也可以通过缩放卷积权值来实现:
$$\begin{array}{c}{w}_{ijk}^{\prime }=s_i\cdot w_{ijk},\end{array}$$其中$w$和$w^{\prime }$分别是原始权重和调制权重，$s_i$是对应于第$i$个输入特征图的尺度，$j$和$k$分别枚举卷积的输出特征图和空间足迹。

现在，实例归一化的目的就是从本质上去除卷积输出特征映射的统计数据中s的影响。
我们认为，这一目标可以更直接地实现。
假设输入激活是具有单位标准差的独立同分布i.i.d.随机变量。
调制卷积后，输出激活量的标准差为
$$\begin{array}{c}{\sigma }_j=\sqrt{\sum _{i,k}{w_{ijk}^{\prime }}^2},\end{array}$$即，输出按相应权重的 $L_2$ 范数缩放。随后的归一化旨在将输出恢复到单位标准差。
根据方程2，如果我们将每个输出特征图 $j$ 缩放（“解调”）$1/{\sigma }_j$，就可以实现这一点。
或者，我们可以再次将其烘焙bake到卷积权重中：
$$\begin{array}{c}{w}_{ijk}^{\prime \prime }=w_{ijk}^{\prime }/\sqrt{\sum _{i,k}{w_{ijk}^{\prime }}^2+ϵ},\end{array}$$其中 $ϵ$ 是一个小常数，以避免数值问题。

我们现在已经将整个样式块烘焙baked成一个单独的卷积层，它的权重是根据s使用公式1和公式3进行调整的(图2d)。
与实例归一化相比，我们的解调技术较弱，因为它是基于信号的统计假设，而不是特征图的实际内容。
类似的统计分析在现代网络初始化器中已经被广泛使用[12,16]，但我们没有意识到它以前曾被用来替代依赖数据的标准化。
我们的解调也与权值归一化[32]有关，它执行与重参数化权值张量相同的计算。
之前的工作已经发现，在GAN训练[38]的背景下，权重归一化是有益的。

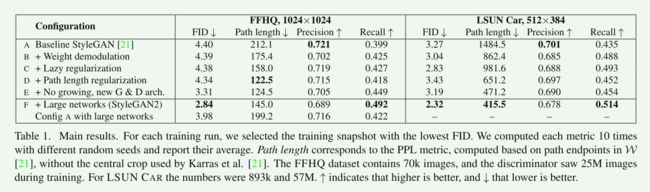
我们的新设计删除了特征伪影（图3)，同时保留了完全的可控性，如随附视频所示。
FID基本上不受影响(表1，行A, B)，但有一个显著的转变，从精度到召回。
我们认为这通常是可取的，因为召回可以通过截断转换为精度，而相反的情况是不正确的[22]。
在实践中，我们的设计可以有效地使用分组卷积来实现，详见附录B。
为了避免不得不考虑方程3中的激活函数，我们缩放了激活函数，以便它们保留预期的信号方差。

3. Image quality and generator smoothness

虽然像FID或精度和召回(P&R)这样的GAN度量标准成功地捕捉到了生成器的许多方面，但它们在图像质量方面仍然存在一定的盲点。
例如，请参考增刊中的图3和图4，将FID和P&R得分相同但总体质量明显不同的生成器进行对比。²

我们观察到感知图像质量和感知路径长度(PPL)[21]之间的相关性，感知路径长度是一个最初引入的度量，用于通过测量在潜在空间中的小扰动下生成的图像之间的平均LPIPS距离[44]来量化从潜在空间到输出图像的映射的平滑性。
再次参考增补中的图3和图4，一个更小的PPL（更平滑的生成器映射）似乎与总体图像质量的较高相关，而其他度量对此变化视而不见。
图4通过LSUN CAT上的每幅图像PPL得分，通过对$w\sim f(z)$周围的潜在空间进行采样计算，更仔细地检查了这种相关性。
低分数确实是高质量图像的指示，反之亦然。
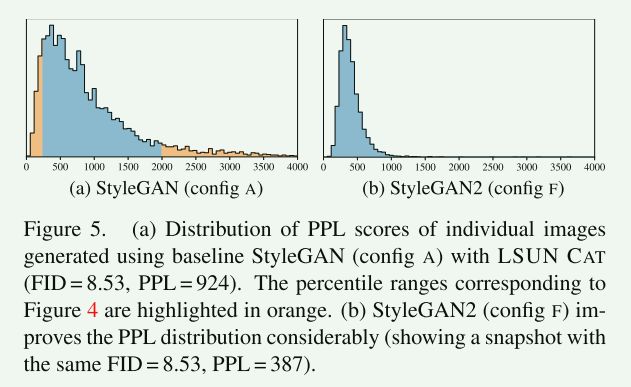
图5a显示了相应的直方图，并揭示了分布的长尾。
模型的总体PPL只是每个图像PPL得分的期望值。
我们总是为整个图像计算PPL，而不是Karras等人。 [21]他们使用较小的中央裁剪。

为什么低PPL与图像质量相关还不是很明显。
我们假设，在训练过程中，由于鉴别器对破碎图像进行惩罚，生成器最直接的改进方式就是有效地拉伸产生好图像的潜在空间区域。
这将导致低质量的图像被压缩到快速变化的小潜在空间区域。
虽然这在短期内提高了平均输出质量，但累积的失真损害了训练的动态，从而最终的图像质量。

显然，我们不能简单地鼓励最小PPL，因为这将引导生成器走向零召回的退化解决方案。
相反，我们将描述一个新的正则化器，其目标是在没有这个缺点的情况下实现更平滑的生成器映射。
由于所得到的正则化项的计算有些昂贵，所以我们首先描述一个适用于任何正则化技术的通用优化。

3.1. Lazy regularization

典型地，主损失函数（例如，Logistic损失[13])和正则化项（例如$R_1$[25])被写成一个单一表达式，从而被同时优化。
我们观察到正则化项的计算频率比主损失函数低，从而大大减少了它们的计算成本和总的内存使用。
表1的C行显示，当每16个小批处理只执行一次R1正则化时，不会造成任何伤害，我们对新的正则化器也采用了相同的策略。 附录B给出了实施细节。

3.2. Path length regularization

我们鼓励 $\mathcal{W}$ 中的固定大小步骤导致图像中非零、固定幅度的变化。
我们可以通过步入图像空间中的随机方向并观察相应的 $\mathrm{w}$ 梯度来凭经验测量与理想值的偏差。
无论 $\mathrm{w}$ 或图像空间方向如何，这些梯度都应该具有接近相等的长度，这表明从潜在空间到图像空间的映射是条件良好的{Odena2018}。

在单个 $\mathrm{w}\in \mathcal{W}$ 处，生成器映射 $g(\mathrm{w})$ 的局部度量缩放属性： $\mathcal{W}\mapsto \mathcal{Y}$由雅可比矩阵 ${\mathbf{J}}_{\mathrm{w}}=\partial g(\mathrm{w})/\partial \mathrm{w}$ 捕获。
出于无论方向如何都保留向量的预期长度的愿望，我们将正则化器表示为
E w , y ∼ N ( 0 , I ) ( ∥ J w T y ∥ 2 − a ) 2 , \begin{equation} \mathbb{E}_{\mathrm{w}, \mathrm{y} \sim \mathcal{N}(0, \mathbf{I})} \left(\left\lVert \mathbf{J}_\mathrm{w}^T \mathrm{y}\right\rVert_2 - a\right)^2, \end{equation} Ew,y∼N(0,I)​( ​JwT​y ​2​−a)2,​​其中$\mathrm{y}$是具有正态分布像素强度的随机图像，$\mathrm{w}\sim f(\mathbf{z})$，其中$\mathbf{z}$是正态分布的。我们在 Appendix C 中表明，在高维度中，当 ${\mathbf{J}}_{\mathrm{w}}$ 在任何 $\mathrm{w}$ 处正交（在全局范围内）时，该先验最小化。
正交矩阵保留长度并且不会沿任何维度引入挤压。

为了避免雅可比矩阵的显式计算，我们使用恒等式 ${\mathrm{J}}_{\mathrm{w}}^T\mathrm{y}={\nabla }_{\mathrm{w}}(g(\mathrm{w})\cdot \mathrm{y})$，可以使用标准反向传播 {Dauphin2015} 进行有效计算。
常数 $a$ 在优化期间动态设置为长度 $\Vert {\mathrm{J}}_{\mathrm{w}}^T\mathrm{y}{\Vert }_2$ 的长期指数移动平均值，允许优化本身找到合适的全局尺度。

我们的正则化器与 Odena 等人{Odena2018} 提出的雅可比clamping正则化器密切相关。
实际差异包括我们以分析方式计算乘积 ${\mathrm{J}}_{\mathrm{w}}^T\mathrm{y}$，而他们使用有限差分来估计 ${\mathbf{J}}_{\mathrm{w}}\mathbf{\delta }$ 与 $\mathcal{Z}\ni \mathbf{\delta }\sim \mathcal{N}(0,\mathbf{I})$。
应该注意的是，生成器{Zhang2018sagan}的谱归一化{Miyato2018B}仅约束最大奇异值，对其他值没有限制，因此不一定会导致更好的调节。
我们发现，除了我们的贡献之外，启用光谱归一化-----或者代替它们--------总是会损害 FID，如 Appendix E 中详述。

在实践中，我们注意到路径长度正则化可以带来更可靠且一致的行为模型，从而使架构探索变得更容易。
我们还观察到更平滑的生成器更容易反转（第5节 ）。
图5b显示路径长度正则化明显收紧了每个图像PPL得分的分布，而不会将模式推到零。
然而，表1的第D行指出了在结构不如FFHQ的数据集中FID和PPL之间的折衷。

4. Progressive growing revisited

渐进式生长[20]在稳定高分辨率图像合成方面非常成功，但它引起了自己的特征伪影。
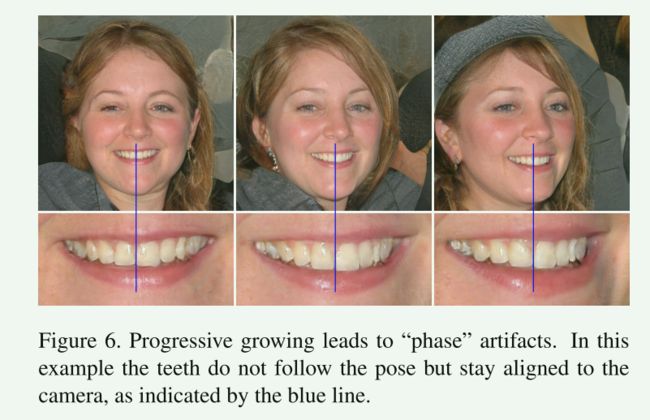
关键问题是，逐渐增长的生成器似乎对细节有强烈的位置偏好； 伴随的视频显示，当牙齿或眼睛等特征应该在图像上平稳移动时，它们可能会在跳到下一个首选位置之前保持原地不动。
图6显示了一个相关的伪影。
我们认为问题在于，在渐进增长中，每个分辨率暂时用作输出分辨率，迫使它产生最大的频率细节，然后导致训练的网络在中间层中具有过高的频率，损害了移位不变性[43]。
附录A显示了一个例子。 这些问题促使我们寻找一种替代的提法，既保留逐步增长的好处，又没有这个缺点。

4.1. Alternative network architectures

虽然StyleGAN在生成器（合成网络）和鉴别器中使用简单的前馈设计，但有大量的工作致力于研究更好的网络架构。
跳过连接[29,19]、残差网络[15,14,26]和分层方法[6,41,42]在生成方法中也被证明是非常成功的。
因此，我们决定重新评估StyleGAN的网络设计，并寻找一种不需要渐进增长就能产生高质量图像的架构。

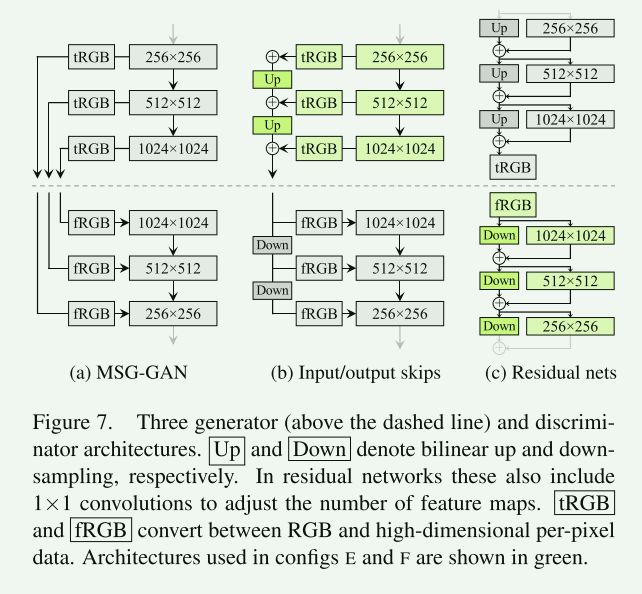
图7a显示了MSG-GAN[19]，它使用多个跳过连接连接生成器和鉴别器的匹配分辨率。
修改MSG-GAN生成器以输出mipmap[37]而不是图像，并且对于每个实际图片也计算类似的表示。
在图7b中，我们通过上采样并求和对应于不同分辨率的RGB输出的贡献来简化此设计。
在鉴别器中，我们类似地将下采样图像提供给鉴别器的每个分辨率块。
我们在所有上、下采样操作中都使用双线性滤波。
在图7c中，我们进一步修改设计，使用剩余连接。³
这种设计类似于LAPGAN[6]，没有Denton等人使用的每分辨率鉴别器。

表2比较了三种生成器和三种鉴别器体系结构：StyleGAN中使用的原始前馈网络、跳过连接和残差网络，所有这些都是在没有渐进增长的情况下训练的。
为9种组合中的每一种提供了FID和PPL。
我们可以看到两个广泛的趋势：在所有配置中，生成器中的跳过连接极大地改善了PPL，残差鉴别器网络显然有利于FID。
后者也许并不奇怪，因为鉴别器的结构类似于分类器，在分类器中残差结构是已知的有用结构。
然而，在生成器中residual架构是有害的-----唯一的例外是LSUN汽车中的FID，当两个网络都是residual时。

对于本文的其余部分，我们使用skip生成器和残差residual鉴别器，而不是渐进增长。 这与表1中的配置E相对应，它显著改善了FID和PPL。

4.2. Resolution usage

我们希望保留的渐进增长的关键方面是，生成器最初将关注低分辨率的特征，然后慢慢地将注意力转移到更精细的细节上。
图7中的体系结构使得生成器可以首先输出不受高分辨率层显著影响的低分辨率图像，然后随着训练的进行将焦点转移到高分辨率层。
因为这不是以任何方式强制执行的，所以生成器只会在有益的情况下才会这样做。
为了分析实践中的行为，我们需要量化生成器在训练过程中对特定分辨率的依赖程度。

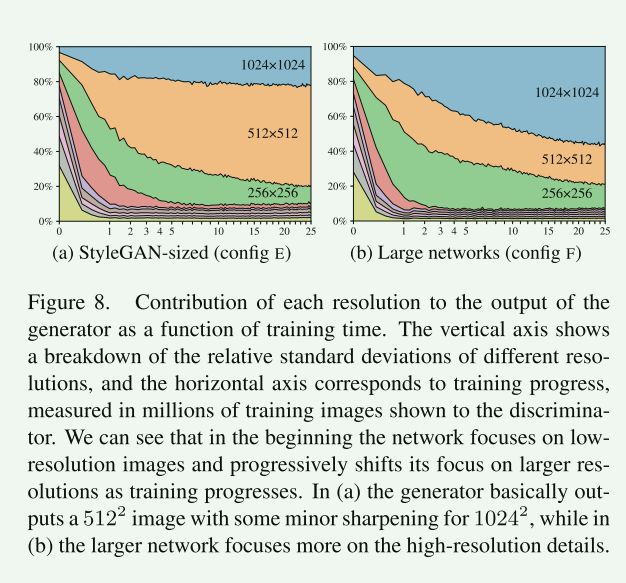
由于跳过生成器（图7b)通过显式地对来自多个分辨率的RGB值求和来形成图像，我们可以通过测量相应层对最终图像的贡献来估计它们的相对重要性。
在图8a中，我们绘制了每个TRGB层产生的像素值的标准偏差作为训练时间的函数。
我们计算了w的1024个随机样本的标准差，并将其归一化，使之和为100%。

在训练开始时，我们可以看到新的跳过生成器的行为类似于渐进增长–现在在不改变网络拓扑的情况下实现。
因此，期望最高分辨率在训练接近尾声时占据主导地位是合理的。
然而，该图显示，这在实践中没有发生，这表明生成器可能无法“充分利用”目标分辨率。
为了验证这一点，我们手动检查了生成的图像，并注意到它们通常缺乏训练数据中存在的一些像素级细节–这些图像可以被描述为512²图像的锐化版本，而不是真正的1024²图像。

这使我们假设我们的网络中存在容量问题，我们通过在两个网络的最高分辨率层中增加一倍的特征映射来测试它。⁴
这使得行为更符合预期：图8b显示了最高分辨率层的贡献显著增加，表1的F行显示了FID和召回显著改善。
最后一行显示基线StyleGAN也受益于额外的容量，但它的质量仍然远低于StyleGAN2。

表3将StyleGAN和StyleGAN2在四个LSUN类别中进行了比较，再次显示了FID的明显改善和PPL的显著进步。 规模的进一步增加可能会带来额外的好处。

5. Projection of images to latent space

合成网络 g 的反演是一个有趣的问题，有着广泛的应用。
在潜在特征空间中操作给定图像首先需要为其找到一个匹配的潜在代码w。
以前的研究[1,9]表明，如果为生成器的每一层选择一个单独的w，结果将得到改善，而不是找到一个共同的潜在代码w。
在早期的编码器实现中使用了相同的方法[27]。
在以这种方式扩展潜在空间找到与给定图像更接近的匹配的同时，它还能够投影不应该具有潜在表示的任意图像。
相反，我们专注于在原始的、未扩展的潜在空间中寻找潜在代码，因为这些代码对应于生成器可能产生的图像。

我们的投影方法在两个方面不同于以前的方法。
首先，为了更全面地挖掘潜在的空间，我们在优化过程中对潜在的编码加入了斜降ramped-down噪声。
其次，我们还对StyleGAN生成器的随机噪声输入进行了优化，将它们正则化，以确保它们最终不会携带相干coherent信号。
正则化是基于增强噪声映射的自相关系数，以匹配多个尺度上的单位高斯噪声的自相关系数。
我们的投影方法的细节可以在附录D中找到。

对被操纵或生成的图像进行检测是一个非常重要的任务。 目前，基于分类器的方法可以相当可靠地检测生成的图像，而不管它们的确切来源[24,39,35,45,36]。 然而，鉴于生成方法的快速进展，这种情况可能不会持久。 除了一般的假图像检测之外，我们还可以考虑这个问题的一个更有限的形式：能够将假图像归因于其特定的来源[2]。 对于StyleGAN，这相当于检查是否存在重新合成所讨论的图像的w∈W。

5.1. Attribution of generated images

检测被操纵或生成的图像是一项非常重要的任务。
目前，基于分类器的方法可以非常可靠地检测生成的图像，无论其确切来源如何{Li2018，Yu2018，Wang2019，Zhang2019ganartifacts，Wang2019b}。
然而，鉴于生成方法的快速进步，这种情况可能不会持续下去。
除了对假图像的一般检测之外，我们还可以考虑问题的更有限的形式：能够将假图像归因于其特定来源{Albright2019}。
对于 StyleGAN，这相当于检查是否存在一个$\mathrm{w}\in \mathcal{W}$来重新合成所讨论的图像。

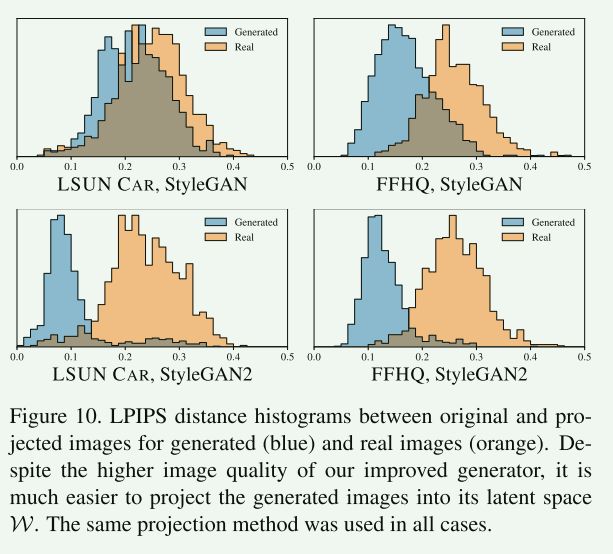
我们通过计算原始图像和重新合成图像之间的 LPIPS{Zhang2018metric} 距离来衡量投影的成功程度。
公式为$D_{\mathrm{LPIPS}}[\mathbf{x},g({\tilde{g}}^{-1}(\mathbf{x}))]$，其中$\mathbf{x}$ 是正在分析的图像${\tilde{g}}^{-1}$表示近似投影操作。
图 10 显示了使用原始 StyleGAN 和 StyleGAN2 的 LSUN Car 和 FFHQ 数据集的这些距离的直方图，以及图 9 显示了示例投影。
使用 StyleGAN2 生成的图像可以很好地投影到 $\mathcal{W}$ 中，以至于它们几乎可以明确地归因于生成网络。
然而，对于原始的 StyleGAN，即使技术上应该可以找到匹配的潜在代码，但从 $\mathcal{W}$ 到图像的映射似乎过于复杂，以至于在实践中无法可靠地成功。
我们发现令人鼓舞的是，尽管图像质量已显着提高，但 StyleGAN2 使来源归因变得更加容易。

6. Conclusions and future work

我们已经在StyleGAN中识别和修复了一些图像质量问题，进一步提高了质量，并大大提高了几个数据集的技术水平。
在某些情况下，在运动中可以更清楚地看到这些改进，如所附的视频所示。
附录A包含了使用我们的方法可以得到的结果的进一步例子。
尽管质量有所改善，但StyleGAN2使生成的图像更容易归属于其来源。

训练成绩也有所提高。在1024² 的分辨率下，原始的StyleGAN(表1中的配置A)在NVIDIA DGX-1和8个Tesla V100 GPUs,上以每秒37张图像的速度运行，而我们的配置E以61 img/s的速度运行，速度快了40%。
由于权重解调、延迟正则化和代码优化，大多数加速来自简化的数据流。
StyleGAN2(配置F，更大的网络)以31 img/s的速度训练，因此只比原来的StyleGAN稍微贵一点。
它的总训练时间为9天FFHQ和13天LSUN CAR。

整个项目，包括所有勘探，耗电量132 MWh，其中0.68 MWh用于训练最终的FFHQ模型。总的来说，我们使用了大约51个单GPU年的计算(Volta类GPU)。更详细的讨论见附录F。

在未来，研究路径长度正则化的进一步改进可能会有成果，例如，用数据驱动的特征空间度量取代像素空间L2距离。
考虑到GANs的实际部署，我们认为找到减少训练数据需求的新方法是很重要的。
这在获取数万个训练样本是不可行的，并且数据集包含大量内在变化的应用中尤其重要。

---

1. 在极少数情况下(可能是0.1%的图像)，液滴丢失，导致图像严重损坏。详情请参见附录A。 ↩︎

2. 我们认为，这种明显不一致的关键在于特征空间的选择，而不是FID或P&R的基础。 最近发现，使用ImageNet[30]训练的分类器往往更多地基于纹理而不是形状[10]，而人类强烈地关注形状[23]。 这在我们的上下文中是相关的，因为FID和P&R分别使用了InceptionV3[34]和VGG-16[34]中的高级特征，这些特征是以这种方式训练的，因此期望偏向于纹理检测。 因此，具有例如强猫纹理的图像彼此可能看起来比人类观察者所同意的更相似，因此部分地损害了基于密度的度量(FID)和流形覆盖度量(P&R)。 ↩︎

3. 在剩余网络架构中，两条路径的相加会导致信号方差的倍增，我们通过乘以$1/\sqrt{2}$来抵消该方差。 这对于我们的网络是至关重要的，而在分类resnets[15]中，这个问题通常被批处理规范化所隐藏。 ↩︎

4. 我们将64²-1024²分辨率的特征图数量增加了一倍，同时保持网络的其他部分不变。 这使得生成器中的可训练参数总数增加了22%(25M→30M)，鉴别器中的可训练参数总数增加了21%(24M→29M)。 ↩︎