线性回归:异方差检测及其处理方法
1.异方差的定义
1.1 定义
对于经典线性回归模型 Y i = β 0 + β 1 X 1 i + β 2 X 2 i + ⋯ + β n X n i + u i Y_{i}=\beta_{0}+\beta_{1}X_{1i}+\beta_{2}X_{2i}+\dots+\beta_{n}X_{ni}+u_{i} Yi=β0+β1X1i+β2X2i+⋯+βnXni+ui在其他假设不变条件下,若随机误差项 u i u_{i} ui的方差不相等,即 V a r ( u i ∣ X 1 i , X 2 i , … , X n i ) = σ i 2 Var(u_{i}|X_{1i},X_{2i},\dots,X_{ni})=\sigma_{i}^{2} Var(ui∣X1i,X2i,…,Xni)=σi2则称随机误差项(即总体方差) u i u_{i} ui具有异方差性。
1.2 影响
异方差性的存在,会对回归模型的正确建立和统计推断带来严重后果。首先,在异方差情况下,所有与参数估计量方差有关的相关计算都会受到影响。 t t t检验、多元回归的 F F F检验都会因此变得不再准确。其次,异方差条件下参数的OLS估计量不再有效(仍然具有线性和一致性),会导致对 Y Y Y的预测也失去有效性。
1.3 产生原因
异方差产生的原因大致可以归纳为以下几种情况,具体如下:
- 解释变量变化对被解释变量所产生影响的程度不断变化,会引起异方差性;
- 遗漏变量或模型形式设定偏误都可能会产生异方差性。当遗漏的变量与解释变量相关时,其对被解释变量的影响被归入随机误差项,则可能使随机误差项产生异方差性。当模型形式设定偏误时,如变量间本来为非线性关系,而错误的设定为线性关系时,则该模型往往表现出异方差性。
- 样本数据本身属性也会导致异方差性;
2. 异方差的检测
异方差性表现为解释变量与随机干扰项方差之间的某种关系。具体常用的几种检测方法如下:
2.1 图示法
该方法的做法主要是通过绘制某个解释变量与样本残差平方 e i 2 e_{i}^{2} ei2的散点图,查看这两者之间是否存在某种关系。如果不存在异方差性,则 e i 2 e_{i}^{2} ei2不会随着 X X X的变化而变化,若 e i 2 e_{i}^{2} ei2会随着 X X X的变化而发生同步变化,则可以初步判断模型存在异方差性。
2.2 G-Q检验
G-Q检验又称为样本分段检验,该检验可用于检验递增性或递减性异方差的有效方法。该方法的检验思路是,若随机干扰项方差随着某解释变量的增加同步递增或递减,则将该解释变量按大小排序之后,分成两段,则前后两段的残差平方和的差别会较大。其具体步骤如下:
- 将样本观测值按照认为可能会引起异方差的某个解释变量观测值的大小排序;如果是时间序列数据,则不可以排序;
- 将序列中间不大于 1 / 3 1/3 1/3观测总量的观测值删除。此时序列形成前后两段,记其前后两段的样本容量分别为 n 1 n_{1} n1、 n 2 n_{2} n2。为计算方便,一般设置 n 1 = n 2 n_{1}=n_{2} n1=n2。
- 分别用OLS方法对前后两段数据进行回归,可以得到两个回归模型各自的残差,分别记为 e 1 i e_{1i} e1i、 e 2 i e_{2i} e2i。则这两个回归模型的残差平方分别为 R S S 1 = ∑ i = 1 n 1 e i 1 2 RSS_{1}=\sum_{i=1}^{n_{1}}e_{i1}^{2} RSS1=∑i=1n1ei12、 R S S 2 = ∑ i = 1 n 2 e i 2 2 RSS_{2}=\sum_{i=1}^{n_{2}}e_{i2}^{2} RSS2=∑i=1n2ei22
- 分别计算前后两个回归模型随机误差项方差的估计量 σ ^ 1 2 = R S S 1 n 1 − k \hat \sigma_{1}^{2}=\frac{RSS_{1}}{n_{1}-k} σ^12=n1−kRSS1、 σ ^ 2 2 = R S S 2 n 2 − k \hat \sigma_{2}^{2}=\frac{RSS_{2}}{n_{2}-k} σ^22=n2−kRSS2,其中 k k k为模型参数的个数。将大方差设为分子,小方差设为分母。由此构建检验统计量 F = σ ^ 1 2 σ ^ 2 2 F=\frac{\hat \sigma_{1}^{2}}{\hat \sigma_{2}^{2}} F=σ^22σ^12在同方差假定下, F F F满足自由度为 n 1 − k n_{1}-k n1−k与 n 2 − k n_{2}-k n2−k的 F F F分布。
- 在同方差假定下, σ ^ 1 2 \hat \sigma_{1}^{2} σ^12与 σ ^ 2 2 \hat \sigma_{2}^{2} σ^22应近似相等,即 F F F统计量应接近于1;如果统计量 F F F偏离1越远,则随机干扰项存在异方差性的可能性就越大。在给定显著性水平 α \alpha α下,若 F > F α ( n 1 − k , n 2 − k ) F>F_{\alpha}(n_{1}-k,n_{2}-k) F>Fα(n1−k,n2−k),则拒绝同方差性假定,表明存在异方差性。
2.3 戈里瑟检验
戈里瑟检验的基本思想是用残差绝对值 ∣ e i ∣ |e_{i}| ∣ei∣对每个解释变量建立各种回归模型,比如: ∣ e i ∣ = α 1 + α 2 X i + v i |e_{i}|=\alpha_{1}+\alpha_{2}X_{i}+v_{i} ∣ei∣=α1+α2Xi+vi或 ∣ e i ∣ = α 1 + α 2 1 X i + v i |e_{i}|=\alpha_{1}+\alpha_{2}\frac{1}{X_{i}}+v_{i} ∣ei∣=α1+α2Xi1+vi或 ∣ e i ∣ = α 1 + α 2 X i + v i |e_{i}|=\alpha_{1}+\alpha_{2}\sqrt{X_{i}}+v_{i} ∣ei∣=α1+α2Xi+vi对回归系数 α 2 \alpha_{2} α2进行显著性检验。如果 α 2 ≠ 0 \alpha_{2} \neq0 α2=0,则认为存在异方差性。该检验的缺点是不能判断模型是否不存在异方差,并要求变量的观测值为大样本。
2.4 怀特检验
怀特检验的基本思想是:如果存在异方差,其方法 σ i 2 \sigma_{i}^{2} σi2与解释变量有关系,则可以分析 σ i 2 \sigma_{i}^{2} σi2是否与解释变量有某些形式的联系,以此判断异方差性。其具体步骤如下:
- 使用普通最小二乘法估计模型,并获取样本残差 e i e_{i} ei。
- 构建所有解释变量及其平方项和交叉乘积项对残差平方 e i 2 e_{i}^{2} ei2的线性回归模型,并检验各回归系数是否为0,若所有参数都为0则不存在异方差性。
3. 异方差的修正
通过加权变换使原模型中的异方差误差项转换为同方差误差项,使加权变换后的模型满足最小二乘法的假定,从而使用普通最小二乘法估计参数,这种方法称为加权最小二乘法(Weighted Least Square, WLS)。在实践中可以根据实际情况寻找合适的权进行加权最小二乘法估计。以一元线性回归模型为例进行说明: Y i = β 1 + β 2 X i + u i Y_{i}=\beta_{1}+\beta_{2}X_{i}+u_{i} Yi=β1+β2Xi+ui
3.1 σ i 2 \sigma_{i}^{2} σi2已知
如果每个观测点的误差项方差 σ i 2 \sigma_{i}^{2} σi2是已知的,使用 1 / σ i 1/\sigma_{i} 1/σi为权数,对模型作如下变换即可: Y i σ i = β 1 σ i + β 2 X i σ i + u i σ i \frac{Y_{i}}{\sigma_{i}}=\frac{\beta_{1}}{\sigma_{i}}+\beta_{2}\frac{X_{i}}{\sigma_{i}}+\frac{u_{i}}{\sigma_{i}} σiYi=σiβ1+β2σiXi+σiui
3.2 σ i 2 \sigma_{i}^{2} σi2未知
当 σ i 2 \sigma_{i}^{2} σi2是未知时,可根据模型首次估计的残差与解释变量或被解释变量的关系来确定变换的权数。一般先采用戈里瑟检验方法确定 e i e_{i} ei与 X i X_{i} Xi之间的关系
- 如果 ∣ e i ∣ |e_{i}| ∣ei∣与 X i \sqrt{X_{i}} Xi之间为线性关系,则可对模型两边同时乘以 1 X i \frac{1}{\sqrt{X_{i}}} Xi1,即可将异方差模型变为同方差模型。此时模型为: Y i X i = β 1 X i + β 2 X i + u i X i \frac{Y_{i}}{\sqrt{X_{i}}}=\frac{\beta_{1}}{\sqrt{X_{i}}}+\beta_{2}\sqrt{X_{i}}+\frac{u_{i}}{\sqrt{X_{i}}} XiYi=Xiβ1+β2Xi+Xiui
- 如果 ∣ e i ∣ |e_{i}| ∣ei∣与 X i X_{i} Xi之间为线性关系,则选择 1 X i \frac{1}{X_{i}} Xi1为权数,将其变换为如下模型: Y i X i = β 1 X i + β 2 + u i X i \frac{Y_{i}}{X_{i}}=\frac{\beta_{1}}{X_{i}}+\beta_{2}+\frac{u_{i}}{X_{i}} XiYi=Xiβ1+β2+Xiui
实践中,遇到异方差时,往往分别以 1 X i \frac{1}{X_{i}} Xi1、 1 X i \frac{1}{\sqrt{X_{i}}} Xi1、 1 ∣ e i ∣ \frac{1}{|e_{i}|} ∣ei∣1为权,对原模型进行加权最小二乘法估计,选取最优结果作为最终估计结果。
4 实验
4.1 构造数据
因为没有找到找到符合异方差性的数据,所以这里只能自己构造。这里构造的数据中 Y Y Y与变量 X 1 X_{1} X1之间并不是线性关系。另外,生成 Y Y Y的公式中的各参数是随意设置的。
import pandas as pd
from scipy import stats
import statsmodels.api as sm
import numpy as np
from sklearn.datasets import make_regression
from matplotlib import pyplot as plt
X,_ = make_regression(n_samples=2000, n_features=5,random_state=5)
X=pd.DataFrame(X)
#参数是随便设置的
y=0.2*X[0]+5*(X[1]**2)+0.56*X[2]+2.7*X[3]-1.3*X[4]
y=pd.DataFrame(y,columns=['val'])
X=sm.add_constant(X)
model=sm.OLS(y,X)
results=model.fit()
y_pred=pd.DataFrame(model.predict(results.params,X),
columns=['val'])
print(results.summary())
此时线性回归的结果如下( R 2 R^{2} R2值较低,模型无法用于预测):
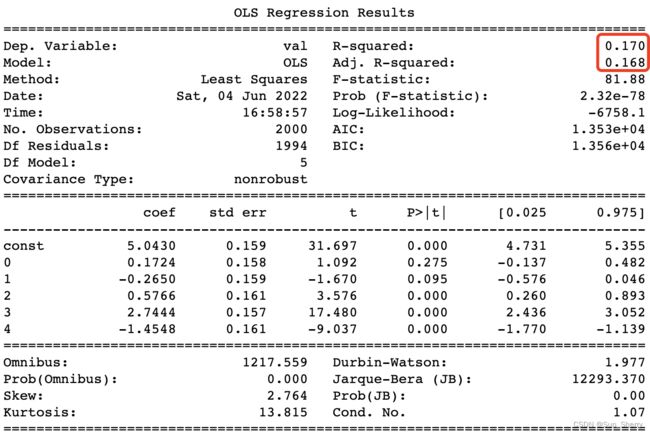
4.2 异方差检测
首先戈里瑟检验、怀特检验都是通过建立相应的回归模型判断是否存在不为0的回归系数来判断是否存在异方差性的。若存在不为0的回归系数则证明有异方差性,否则没有异方差性。而这个判断可以使用OLS模型中各个回归参数的p_val值来判断,若p_val值越接近0,对应的回归系数越显著,该系数为0的可能性越低。对于这两个检验,通过p_val值来观测是否存在异方差性。各种异方差检测方法如下:
图示法
#误差项
err_abs=(y_pred-y).abs()
#1.检验是否存在异方差性
#1.1 图示法
fig,((ax1,ax2),(ax3,ax4))=plt.subplots(nrows=2,ncols=2)
ax1.scatter(X[0],(err_abs)**2)
ax1.set_xlabel('X[0]')
ax2.scatter(X[1],(err_abs)**2)
ax2.set_xlabel('X[1]')
ax3.scatter(X[2],(err_abs)**2)
ax3.set_xlabel('X[2]')
ax4.scatter(X[3],(err_abs)**2)
ax4.set_xlabel('X[3]')
plt.show()
其具体结果如下(从图中可以看到 e i 2 e_{i}^{2} ei2与 X 1 X_{1} X1之间有明确的关系,但不是递增或递减的关系):
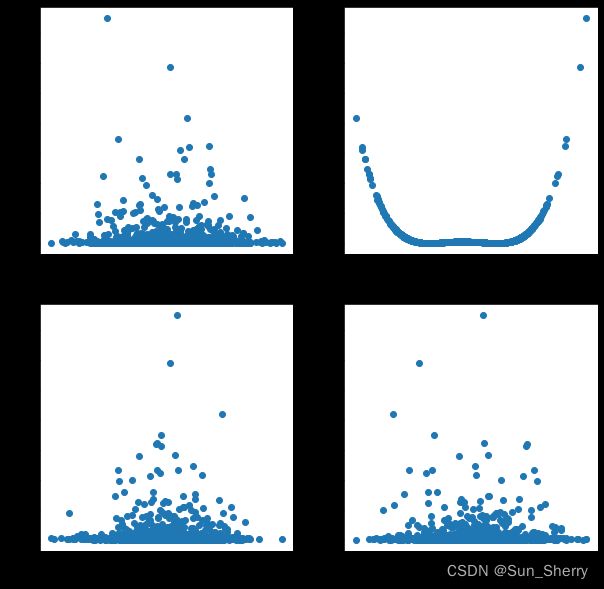
戈里瑟检验
因为各个变量 X i X_{i} Xi值既有正值又有负值,所以这里只判断 ∣ e i ∣ |e_{i}| ∣ei∣与 X i X_{i} Xi、 1 / X i 1/X_{i} 1/Xi之间是否存在线性关系。具体如下:
for col in [0,1,2,3,4]:
print("第{}个变量".format(col))
X_tmp=X[['const',col]]
model_i=sm.OLS(err_abs,X_tmp)
result_tmp=model_i.fit()
print(result_tmp.pvalues)
#判断|e|与1/X之间是否存在线性关系
X_tmp[col]=1/X_tmp[col]
model_i=sm.OLS(err_abs,X_tmp)
result_tmp=model_i.fit()
print(result_tmp.pvalues)
结果如下:

从结果可以看出 ∣ e i ∣ |e_{i}| ∣ei∣与 X 4 X_{4} X4之间存在线性关系。
G-Q检验
从图示法可以看出,样本残差平方与变量 X 1 X_{1} X1之间病并不是递增性型或递减型关系,这里的异方差性并不符合G-Q检验的基本假设。但这里G-Q检验的代码如下:
## G-Q检验
from scipy import stats
for col in [0,1,2,3,4]:
X_tmp=X.sort_values(by=[col],axis=0)
#X共有2000个样本,删除中间650个样本,将剩余样本分为前后两段,各段分别有675个样本
X_head=X_tmp.iloc[:675,:]
X_tail=X_tmp.iloc[-675:,:]
y_head=y.loc[X_head.index]
y_tail=y.loc[X_tail.index]
m_head=sm.OLS(y_head,X_head)
r_head=m_head.fit()
y_pre_head=m_head.predict(r_head.params,X_head)
RSS_head=((y_pre_head-y_head.values)**2).sum()
m_tail=sm.OLS(y_tail,X_tail)
r_tail=m_tail.fit()
y_pre_tail=m_tail.predict(r_tail.params,X_tail)
RSS_tail=((y_tail.values-y_pre_tail)**2).sum()
if RSS_head>RSS_tail:
f_val=(RSS_head/(y_head.shape[0]-5))/(RSS_tail/(y_tail.shape[0]-5))
f_pval=stats.f.sf(f_val,y_head.shape[0]-5,y_tail.shape[0]-5)
else:
f_val=(RSS_tail/(y_tail.shape[0]-5))/(RSS_head/(y_head.shape[0]-5))
f_pval=stats.f.sf(f_val,y_tail.shape[0]-5,y_head.shape[0]-5)
print("对于变量:{},其F值为:{:.3f},p值为:{:.3f}".format(col,f_val,f_pval))
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree = 2)
X_all=poly.fit_transform(X.loc[:,[0,1,2,3,4]])
X_all=pd.DataFrame(X_all,columns=poly.get_feature_names())
y=err_abs**2
White_m=sm.OLS(y,X_all)
result=White_m.fit()
print(result.summary())
其结果如下:

从上述结果中可以发现,构建的模型中存在具有显著性的回归参数,所以存在异方差性。
4.3 修正
这里只使用 1 / X i 1/X_{i} 1/Xi、 1 / ∣ e i ∣ 1/|e_{i}| 1/∣ei∣来对模型进行加权修正。
#2 使用1/|e_i|为权进行修正
X1=X.copy()
for col in X.columns:
X1[col]=X[col]/err_abs['val']
y1=y['val']/err_abs['val']
model=sm.OLS(y1,X1)
results=model.fit()
print(results.summary())
其最终结果如下:
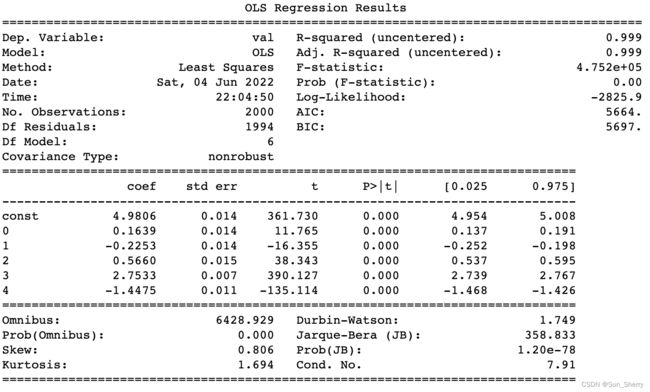
通过戈里瑟检测可以发现 ∣ e i ∣ |e_{i}| ∣ei∣与 X 4 X_{4} X4之间存在线性关系,所以这里使用 1 / X 4 1/X_{4} 1/X4为权进行修正
# 使用1/X4为权进行修正
X2=X.copy()
for col in X.columns:
X2[col]=X[col]/X[4]
y2=y['val']/X[4].values
model=sm.OLS(y2,X2)
results=model.fit()
print(results.summary())
参考
- 《计量经济学》

