7.数组(一维数组、二维数组、C99中的变长数组、二分查找法)
数组
-
- 1.数组的概念
- 2.一维数组
-
- 2.1 一维数组的创建
- 2.2 一维数组的类型
- 2.3 一维数组的初始化
- 2.4 一维数组的下标
- 2.5 一维数组的输入与输出
- 2.6 一维数组在内存中的存储
- 2.7 利用sizeof()计算数组元素的个数
- 3.二维数组
-
- 3.1 二维数组的概念
- 3.2 二维数组的创建
- 3.3 二维数组的初始化
- 3.4 二维数组的下标
- 3.5 二维数组的输入与输出
- 3.6 二维数组在内存中的存储
- 3.C99中的变长数组
- 4.二分查找法(也称折半查找法)
1.数组的概念
数组是一组相同类型元素的集合,其特点有
1.数组存放的是1个或者多个数据,但是数组元素个数不能为0
2.数组中存放的多个数据,类型是相同的
数组分为一维数组和多维数组,多为数组一般以二维数组为主。
2.一维数组
2.1 一维数组的创建
格式:数据类型 数组名[常量值];
例 int num[10];
2.2 一维数组的类型
去掉数组名剩下的就是数组类型,例 int num[10]; 其数组类型为int [10]
数组元素的数据类型 可以是char、int、float等 数组内的元素数据类型都相同
2.3 一维数组的初始化
//完全初始化
int num[5] = {1,2,3,4,5};
//不完全初始化,除了1 2 3,剩下的其余元素都默认为0
int num[5] = {1,2,3};
//初始化1 2 3,长度也为3
int num[] = {1,2,3};
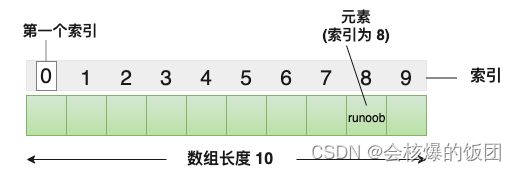
2.4 一维数组的下标
在C语⾔中数组的访问提供了⼀个操作符[ ] ,这个操作符叫:下标引用操作符
注意区分 定义数组时 和 调用数组元素时 [ ] 内常量的区别
定义时里面的常量表示元素的个数
调用时里面的常量表示数组下标,也就是索引位
数组下标是从0开始数起的
举例:
//注意区分 定义数组时 和 访问数组元素时 []的区别
int num[5] = {1,2,3,4,5};//这里num[5]表示的是数组长度为5
printf("数组下标为4的值:%d", num[4]);//这里num[4]表示的是访问数组下标为4的数组元素
2.5 一维数组的输入与输出
输出
//输出
int main() {
int arr[9] = {1,2,3,4,5,6,7,8,9};
for (int i = 0; i < 9; i++)//这里小于9是因为长度为9的数组 下标范围为0~8
{
printf("arr[%d] = %d\n",i,arr[i]);
}
return 0;
}
输入
//输入
int main() {
int arr[9];
for (int i = 0; i < 9; i++)
{
scanf("%d",&arr[i]);
}
for (int i = 0; i < 9; i++)//这里小于9是因为长度为9的数组 下标范围为0~8
{
printf("arr[%d] = %d\n",i,arr[i]);
}
return 0;
}
2.6 一维数组在内存中的存储
一维数组在内存中的存储地址,随着下标增长,由小变大
数组在内存中是连续存放的,以整型数组为例,每两个相邻的数组元素之间相差4(因为一个整型是4个字节)
int main() {
int arr[9] = {1,2,3,4,5,6,7,8,9};
for (int i = 0; i < 9; i++)
{
printf("arr[%d] = %p\n",i,&arr[i]);
}
return 0;
}
16进制的形式表示内存中存储的地址,每个数据元素之间都差4,因为是int类型的数据元素
2.7 利用sizeof()计算数组元素的个数
sizeof()函数是C语言中的一个关键字
作用:计算类型或者变量的大小
单位是字节(byte)
因为数组中的所有元素的数据类型都是相同的,所以每个数据元素的大小相同
即:所占内存空间总大小 / 对应数组元素的数据类型 = 数组内元素的个数
int main() {
int arr[10] = {0};//这里我们就非完全初始化数组,所以我们不知道数组有多少个元素个数
printf("数组 int arr[10] 所占内存空间的总大小:%zd 字节\n",sizeof(arr));
printf("数组 int arr[10] 其中一个数组元素所占内存空间的大小:%zd 字节\n",sizeof(arr[0]));
//所占内存空间总大小 / 对应数组元素的数据类型 = 数组内元素的个数
int sum = sizeof(arr) / sizeof(arr[0]);
printf("数组中元素的个数:%d", sum);
return 0;
}
3.二维数组
3.1 二维数组的概念
二维数组:相当于把一维数组做为数组元素,此时就是二维数组
依此类推,三维数组就是二维数组被做为数组元素的数组
二维数组以上的数组都统称为多维数组
3.2 二维数组的创建
格式:数据类型 数组名[常量值1][常量值2];
例:
int num[10][10];
第一个10表示 数组有10行
第二个10表示 每一行有10个数组元素
3.3 二维数组的初始化
// 不完全初始化
int arr1[3][3] = {1,2,3};
int arr2[3][3] = {0};
// 完全初始化
int arr3[3][3] = {1,2,3, 4,5,6, 7,8,9};
//按照行初始化
int arr4[3][3] = {{1,2,3},{4,5,6},{7,8,9}};
//初始化时可以省略行,但是不能省略列
int arr5[][3] = { 1,2 };
int arr6[][3] = { 1,2,3,4,5};
int arr7[][3] = { {1,2},{4,5},{7,8} };
3.4 二维数组的下标
二维数组中行的下标从0开始,列的坐标也是从0开始
初始化时可以省略行,但是不能省略列
即 int man[可以省略][不能省略];
3.5 二维数组的输入与输出
输入
//输入
for (int i = 0; i < 3; i++)//行号
{
for (int j = 0; j < 3; j++)//列号
{
scanf("%d ", &arr[i][j]);//记得加&
}
}
输出
//输出
for (int i = 0; i < 3; i++)//行号
{
for (int j = 0; j < 3; j++)//列号
{
printf("%d ", arr[i][j]);
}
printf("\n");
}
3.6 二维数组在内存中的存储
二维数组每一行内部的每个元素都是相邻的
以整型为例
每两个相邻的数组元素之间相差4个字节(因为一个整型是4个字节)
跨行连接处的每个元素也都是只差4个字节,所以二维数组在内存中也是连续存放的
int main() {
int arr[3][3] = { {1,2,3},{4,5,6},{7,8,9} };
for (int i = 0; i < 3; i++)//行号
{
for (int j = 0; j < 3; j++)//列号
{
printf("arr[%d][%d] = %p\n", i, j, &arr[i][j]);
}
printf("\n");
}
return 0;
}
3.C99中的变长数组
在C99标准之前,C语言在创建数组的时候,数组大小必须得用常量或常量表达式来表示,或者初始化数组的时候省略数组大小,直接自己输入数组元素。
1.用常量来表示数组大小
int arr[5];
2.省略数组大小,开始直接自己输入元素
int arr[] = {1,2,3,4,5};
这样创建数组会带来非常大的限制,就是数组的大小无法灵活的变化,必须在开始的时候就写死数组的大小。
所有在C99中给定了一个变长数组(variable-length array,简称VLA) 的新特性,允许我们可以使用变量来创建数组大小。
//这样一来就可以根据输入的值来创建对应的大小的数组了
int n;
scanf("%d",&n)
int arr[n];
上述例子中arr为边长数组,它的数组大小取决于输入值n的大小,编译器无法提前确定数组大小,只有程序运行时,才能知道n是多少。(即变长数组的大小只有在运行时才能确定,所以变长数组也就不能初始化)
好处:在开发程序时,不需要特地的去考虑定义数组的大小范围等,程序在运行时可以精确的根据对变量的赋值来分配数组的大小。
注意:程序运行时,根据变量的大小来分配数组的大小,数组的大小一旦被分配,就确定不再变化。(可变是指创建数组时的变量可变,不需要唯一固定值;而不是说能随意的改变数组的大小)
可惜的是在VS2022上支持大部分C99语法,但是VS中不支持C99中的变长数组
#include 输入:
5
1 2 3 4 5输出:
1 2 3 4 5
4.二分查找法(也称折半查找法)
拿传统的查找方法来作比较
就是从数组下标0的元素开始,逐次递增,来和要查找的数进行比较
缺点:如果要查找的数很大,上万上千,那么也要查找上万上千次;查找的数越大查找起来越费劲
//传统查找方式(麻烦,什么年代了还在用传统香。。。方法)
int main() {
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
int k = 0;//要查找的数
int count = 1;//查找次数
scanf("%d", &k);
int sz = sizeof(arr) / sizeof(arr[0]);//数组内元素个数
int find = 0;//假设找不到
int i = 0;
//循环递增数组下标作比较
for (i = 0; i < sz; i++)
{
if (k == arr[i]) {
printf("成功找到arr[%d]=%d,共查找了%d次", i,arr[i],count);
find = 1;
break;
}
count++;
}
if (find == 0)
{
printf("查找了%d次,找不到",count);
}
return 0;
}
二分查找法
开始:
将列表的起始索引 low 设置为 0
将列表的结束索引 high 设置为数组长度减1
循环条件为(low 小于等于 high):
将中间索引 mid 设置为 (low + high) 的一半
如果列表的mid下标对应的元素小于目标值:
将 low 设置为 mid 加 1
如果列表的mid下标对应的元素大于目标值:
将 high 设置为 mid 减 1
否则(也就是low 等于 high 时):
mid 下标对应的元素 等于 目标值
退出循环
//二分查找
int main() {
int arr[] = { 1,2,3,4,5,6,7,8,9,10 };
int k = 0;//要查找的数
scanf("%d", &k);
int count = 1;//查找次数
int find = 0;//假设找不到
int sz = sizeof(arr) / sizeof(arr[0]);//数组内元素个数(组数长度)
//low和high都是指下标位置
int low = 0;
int high = sz - 1;
while (low <= high)
{
int mid = (low + high) / 2;
//以下方法为 int mid = low + high 的优化方法:
//之所以这么写是为了防止数据类型超出上限
//int mid = low + (high - low)/2;
if (arr[mid] < k)
{
low = mid + 1;
count++;
}
else if (arr[mid] > k) {
high = mid - 1;
count++;
}
else
{
printf("成功找到arr[%d]=%d,共查找了%d次", mid, arr[mid], count);
find = 1;
break;
}
}
if (find == 0)
{
printf("找不到");
}
return 0;
}
以int arr[] = { 1,2,3,4,5,6,7,8,9,10 };为例
虽然说传统查找方法6次 二分查找法3次差别不是特别大
但是随着数组的大小变大,二分查找的效率优势会越来越明显