整数规划——第二章 线性规划
整数规划——第二章 线性规划
2.1 凸分析初步
2.1.1 凸集和分离定理
定义2.1 设集合 C ⊆ R n C\sube \R^n C⊆Rn,如果对任意 x , y ∈ C x,y\in C x,y∈C 和 λ ∈ [ 0 , 1 ] \lambda \in [0,1] λ∈[0,1],有
λ x + ( 1 − λ ) y ∈ C , \lambda x+(1-\lambda) y\in C, λx+(1−λ)y∈C,
则称 C C C 为凸集。
在凸几何中,凸集(convex set)是在凸组合下闭合的仿射空间的子集。更具体地说,在欧氏空间中,凸集是对于集合内的每一对点,连接该对点的直线段上的每个点也在该集合内。例如,立方体是凸集,但是任何中空的或具有凹痕的例如月牙形都不是凸集。
定理2.1 设 C ⊆ R n C\sube \R^n C⊆Rn 为非空闭凸集, y ∈ R n , y ∉ C y\in \R^n,y\not\in C y∈Rn,y∈C,则
-
存在唯一的点 x ‾ ∈ C \overline{x}\in C x∈C,使
∣ ∣ x ‾ − y ∣ ∣ = inf { ∣ ∣ x − y ∣ ∣ ∣ x ∈ C } ||\overline{x}-y|| = \inf \{||x-y||\ |\ x\in C \} ∣∣x−y∣∣=inf{∣∣x−y∣∣ ∣ x∈C}在数学符号中,“inf"代表"infimum”,这是数学分析和集合论中的一个概念。某一集合的infimum是该集合的下界中最大的实数。简单来说,它是小于等于该集合中所有数的最小实数。
该定理表明非空闭凸集中存在与给定点 y y y 最近的点,并且这个点是唯一的。
-
x ‾ ∈ C \overline{x}\in C x∈C 为点 y y y 到集合 C C C 的最近点充要条件是
( x − x ‾ ) T ( x ‾ − y ) ≥ 0 , ∀ x ∈ C (2.1) (x-\overline{x})^T(\overline{x}-y)\ge 0,\quad \forall x\in C\tag{2.1} (x−x)T(x−y)≥0,∀x∈C(2.1)
定理2.2 凸集分离定理 设 C ⊆ R n C\sube \R^n C⊆Rn 为非空闭凸集, y ∈ R n , y ∉ C y\in \R^n,y\not\in C y∈Rn,y∈C,则存在非零向量 a ∈ R n a\in R^n a∈Rn 和数 β \beta β 使得
a T x ≤ β < a T y , ∀ x ∈ C a^\text{T}x\le\beta
具体来说:
- a a a 是一个非零向量,它定义了一个超平面。
- β \beta β 是一个实数,它表示超平面在 a T x a^\text{T}x aTx 方向上的偏移量。
- 对于集合 C C C 中的所有点 x x x,它们都位于这个超平面的一侧,并且超平面分离了点 y y y 和集合 C C C 。
这个定理直观地说明了在凸集 C C C 和点 y y y 之间存在一个超平面,将点 y y y 与集合 C C C 完全分开,即点 y y y 在超平面的一侧,而集合 在另一侧 C C C 。这个超平面可以看作是一条线( n = 2 n=2 n=2 )或者一个平面( n = 3 n=3 n=3)或者更高维空间中的超平面。
2.1.2 多面体基本知识
定义2.2 若 S ⊆ R n S\sube R^n S⊆Rn 是有限多个半空间之交,则称 S S S 为多面体,即 S = { x ∈ R n ∣ a i T ≤ b i , i = 1 , . . . , m } S=\{x\in \R^n |a^T_i \le b_i,\ i=1,...,m\} S={x∈Rn∣aiT≤bi, i=1,...,m},这里 a ∈ R n , a i ≠ 0 , b i ∈ R a∈\R^n,ai≠0,b_i∈\R a∈Rn,ai=0,bi∈R
容易看出,多面体都是闭凸集。设 A ∈ R m × n , b ∈ R m A∈\R^{m\times n},b∈R^m A∈Rm×n,b∈Rm,下面的集合都是多面体:
S = { x ∈ R n ∣ A x ≤ b } , S = { x ∈ R n ∣ A x = b , x ≥ 0 } , S = { x ∈ R n ∣ A x ≤ b , x ≥ 0 } . \begin{aligned} &S=\{x\in \R^n| Ax\le b\},\\ &S=\{x\in \R^n| Ax= b,\ x\ge 0\},\\ &S=\{x\in \R^n| Ax\le b,\ x\ge 0\}. \end{aligned} S={x∈Rn∣Ax≤b},S={x∈Rn∣Ax=b, x≥0},S={x∈Rn∣Ax≤b, x≥0}.
多面体为一系列的(有限个)线性等式和不等式的解集。
半空间是由超平面和它在一个特定侧面的所有点构成的区域
定义2.3 设 S ⊆ R n S\sube \R^n S⊆Rn是非空凸集, x ∈ S x∈S x∈S。若对任意 λ ∈ ( 0 , 1 ) \lambda \in (0,1) λ∈(0,1)和 x 1 , x 2 ∈ S x_1,x_2∈S x1,x2∈S, x = λ x 1 十 ( 1 一 λ ) x 2 x=\lambda x_1十(1一\lambda)x_2 x=λx1十(1一λ)x2可推出 x 1 = x 2 = x x_1=x_2=x x1=x2=x ,则称 x x x 为 S S S 的顶点。
即若 C C C 中不存在任何两个不同的点,使 x x x 成为这两个点连线上的一个点,则 x x x 为顶点。
定义2.4 设 S ⊆ R n S\sube \R^n S⊆Rn是非空凸集, d ∈ R n d\in \R^n d∈Rn。若对任意 x ∈ S x∈S x∈S 和 λ ≥ 0 \lambda \ge 0 λ≥0 都有 x + λ d ∈ S x+λd∈S x+λd∈S,则称 d d d 为 S S S 的一个方向。若对任意 λ 1 , λ 2 > 0 \lambda_1,\lambda_2>0 λ1,λ2>0和 S S S 的方向 d 1 , d 2 d_1,d_2 d1,d2 ,由 d = λ 1 d 1 + λ 2 d 2 d=\lambda_1d_1+\lambda_2d_2 d=λ1d1+λ2d2可推出 d 1 = α d 2 d_1=\alpha d_2 d1=αd2,其中 α > 0 \alpha>0 α>0,则称 d d d 为 S S S 的极方向。(若 S S S 的方向 d d d 不能表示为该集合的两个不同方向的正的线性组合,则称 d d d 为 S S S 的极方向。)
直观上来说,极方向可以看作是在凸集 S S S 的边界点 x 0 x_0 x0 处的“最远延伸方向”。在极方向上,你可以在该方向上无限远地向外延伸,而仍然保持在凸集 S S S 内部。
定理2.3 设 S = { x ∈ R n ∣ A x = b , x ≥ 0 } S=\{x\in \R^n|Ax=b,x\ge0\} S={x∈Rn∣Ax=b,x≥0},其中 A A A 行满秩,则 x ∈ S x\in S x∈S 是 S S S 的顶点的充要条件为 x x x 可以表示为 $ x = \left( \begin{aligned} &B^{-1}b \cr &0 \end{aligned} \right)$,其中 A = ( B , N ) A=(B,N) A=(B,N), B B B 可逆且 B − 1 b ≥ 0 B^{-1}b\ge 0 B−1b≥0
定理2.4 设 S = { x ∈ R n ∣ A x = b , x ≥ 0 } S=\{x\in \R^n|Ax=b,x\ge 0\} S={x∈Rn∣Ax=b,x≥0} 非空,其中 A A A 行满秩,则 S S S 至少有一个顶点。
2.2 线性规划与原始单纯形法
考虑线性规划(Linear Programming,LP)的标准形式:
( L P ) min { c T x ∣ A x = b , x ≥ 0 } (LP)\quad \min\{c^{\text{T}}x|Ax = b,x\ge 0\} (LP)min{cTx∣Ax=b,x≥0}
此处 A ∈ R m × n A\in R^{m\times n} A∈Rm×n, A A A 行满秩,设 S = { x ∈ R n ∣ A x = b , x ≥ 0 } S=\{x\in \R^n | Ax = b, x\ge 0\} S={x∈Rn∣Ax=b,x≥0},称 S S S 为 (LP) 的可行域。
在线性方程组求解中,行满秩矩阵往往具有唯一解。
定理 2.7 (线性规划基本定理)设线性规划可行域 S S S 非空, S S S 的顶点为 x 1 , . . . , x k x_1,...,x_k x1,...,xk ,极方向为 d i , . . . , d l d_i,...,d_l di,...,dl,则(LP)有有限最优解的充要条件为 c T d i ≥ 0 , i = 1 , . . . , l c^Td_i≥0,i=1,...,l cTdi≥0,i=1,...,l。若(LP)有有限最优解,则(LP)必在其中一个顶点 x j x_j xj 上达到最优.
定义2.5 考虑线性规划(LP)的可行域 S S S ,设 A = ( B , N ) A=(B,N) A=(B,N) ,其中 B B B 可逆,则称 B B B 为 A A A 的一个基, x = ( x B x N ) = ( B − 1 b 0 ) x =\left( \begin{aligned} &x_B \cr &x_N \end{aligned} \right)= \left( \begin{aligned} &B^{-1}b \cr &0 \end{aligned} \right) x=(xBxN)=(B−1b0)为 A x = b Ax=b Ax=b 的基本解, x B x_B xB 称为基变量, x N x_N xN 为非基变量。若 B − 1 b ≥ 0 B^{-1}b\ge 0 B−1b≥0,则称 B B B 为原始可行基, x = ( B − 1 b 0 ) x = \left( \begin{aligned} &B^{-1}b \cr &0 \end{aligned} \right) x=(B−1b0) 称为基本可行解。
可知矩阵 A A A 是 m × n m\times n m×n 的矩阵,这里我们假设 A A A 是行满秩(即每行等式都是有意义的),且 m < n m
m<n ,则 A A A 的基向量有 m m m 个。我们把A按列重新排列,表示成 A = ( B , N ) A=(B,N) A=(B,N),其中 B B B 由 m m m 个基向量表示, N N N 由其他 n − m n-m n−m 个非基向量组成。相应的, x x x也可以表示成基变量和非基变量的组合 x = ( x B x N ) x =\left( \begin{aligned} &x_B \cr &x_N \end{aligned} \right) x=(xBxN),目标函数表示为 c B T x B + c N T x N c_B^Tx_B+c_N^Tx_N cBTxB+cNTxN 。对于等式 A x = b Ax=b Ax=b ,可以表示成 B x B + N x N = b Bx_B+Nx_N=b BxB+NxN=b 。非基变量 x N x_N xN 全部取值为0得到的解称之为基解,基解的个数最多为 C n m C_n^m Cnm,若 x > 0 x>0 x>0,则称之为基本可行解。
假设2.1(非退化假设) 对任意基本可行解 x = ( B − 1 b 0 ) x = \left( \begin{aligned} &B^{-1}b \cr &0 \end{aligned} \right) x=(B−1b0),都有 B − 1 b > 0 B^{-1}b> 0 B−1b>0
性质2.1 线性规划的可行域S的顶点和基本可行解一一对应,线性规划若有有限最优解,则一定存在基本可行解是最优解。
上述定理和性质表明,我们只需在可行域的顶点中寻找线性规划的最优解.
单纯形法
单纯形:n维空间内有n+1个顶点的多面体
算法2.1 原始单纯形算法
步0:计算初始基本可行基 B B B 和对应的基本可行解 x = ( B − 1 b 0 ) x = \left( \begin{aligned} &B^{-1}b \cr &0 \end{aligned} \right) x=(B−1b0)。
步1:如果 r N = c N T − c B T B − 1 N ≥ 0 r_N=c_N^T-c_B^TB^{-1}N\ge 0 rN=cNT−cBTB−1N≥0,停止,当前基本可行解 x x x 是最优解,否则,转步2.
步2:选取 j j j 满足 c j − c B T B − 1 a j < 0 c_j-c_B^TB^{-1}a_j<0 cj−cBTB−1aj<0,若 a ‾ j = B − 1 a j ≤ 0 \overline{a}_j=B^{-1}a_j\le 0 aj=B−1aj≤0 停止,原问题无界;否则,转步3.
步3:由 下式 计算 λ \lambda λ ,令 x : = x + λ d j x:=x+\lambda d_j x:=x+λdj,其中 d j = ( − B − 1 a j e j ) d_j=\left( \begin{aligned} &-B^{-1}a_j \\&\qquad e_j \end{aligned} \right) dj=(−B−1ajej),转步1
λ = min { b ‾ i a ‾ i j ∣ a ‾ i j > 0 } = b ‾ r a ‾ r j ≥ 0 \lambda=\min\left\{\frac{\overline{b}_i}{\overline{a}_{ij}}|\overline{a}_{ij}>0\right\}=\frac{\overline{b}_r}{\overline{a}_{rj}}\ge 0 λ=min{aijbi∣aij>0}=arjbr≥0
内在思路:首先我们可以确定一组基,然后通过这一组基求出基可行解。这是0-1步的工作,当我们求出了基可行解之后,我们还需要判断它是不是最优解,这就是2步的工作最优性检验。假设我们检验后知道,所求的解是最优解,那运气确实很好,倘若不是也没有关系,我们就进入3步换基变量。这样就可以求出新的一组基可行解,再进行最优性检测,直到找到最优解为止
单纯形法就是在任意的n维空间内的单纯形上,从一个顶点移动到另一个更好的顶点。直到找不到更好的顶点时,就说明已经达到最优解。
定理2.8 在非退化假设下,原始单纯形算法有限步终止,或找到(LP)的一个最优解,或判断出(LP)无界。
可以用表格的形式表达上述算法,设 b ≥ 0 b\ge 0 b≥0,设初始可行基为 B B B , A = ( B , N ) A=(B,N) A=(B,N),则单纯形方法一次迭代过程可以在下列表格上进行:
“rhs” 是"right-hand side"(右侧常数)的缩写
例2.1 利用单纯形算法求解下列线性规划
min − 7 x 1 − 2 x 2 s . t . − x 1 + 2 x 2 + x 3 = 4 , 5 x 1 + x 2 + x 4 = 20 , 2 x 1 + 2 x 2 − x 5 = 7 , x ≥ 0 \begin{aligned} &\min -7x_1-2x_2\\ &s.t.-x_1+2x_2+x_3=4,\\ &\quad\quad 5x_1+x_2+x_4=20,\\ &\quad\quad 2x_1+2x_2-x_5=7,\\ &\quad\quad x\ge 0 \end{aligned} min−7x1−2x2s.t.−x1+2x2+x3=4,5x1+x2+x4=20,2x1+2x2−x5=7,x≥0
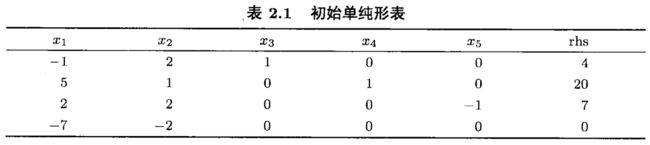
初始单纯形表如下:
第1次迭代。选择初始基 B = ( a 1 , a 3 , a 4 ) B=(a_1,a_3,a_4) B=(a1,a3,a4),以 x B = ( x 1 , x 3 , x 4 ) T x_B=(x_1,x_3,x_4)^T xB=(x1,x3,x4)T 为基变量的单纯形表见下表,其对应的初始基本可行解为 x B = ( x 1 , x 3 , x 4 ) T = ( 3 1 2 , 7 1 2 , 2 1 2 ) , x N = ( x 2 , x 4 ) T = ( 0 , 0 ) T x_B=(x_1,x_3,x_4)^T=(3\frac{1}{2},7\frac{1}{2},2\frac{1}{2}),x_N=(x_2,x_4)^T=(0,0)^T xB=(x1,x3,x4)T=(321,721,221),xN=(x2,x4)T=(0,0)T
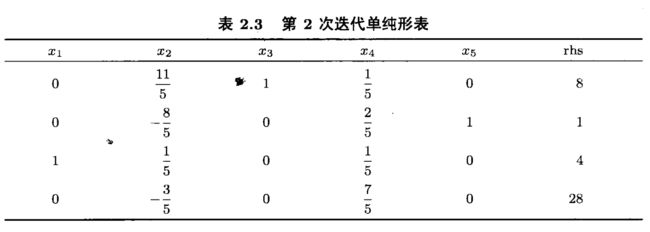
第2次迭代,因 − 7 2 < 0 -\frac{7}{2}<0 −27<0,选择 x 5 x_5 x5 为进基变量,计算 λ = 2 1 2 2 1 2 = 1 \lambda=\frac{2\frac{1}{2}}{2\frac{1}{2}}=1 λ=221221=1,故 x 4 x_4 x4 是离基变量,新的基变量为 x B = ( x 1 , x 3 , x 5 ) x_B=(x_1,x_3,x_5) xB=(x1,x3,x5)。新的单纯形表为表2.3:
第3次迭代,选择 x 2 x_2 x2 为进基变量,计算 min { 8 11 / 5 , 4 1 / 5 } \min\left\{ \frac{8}{11/5},\frac{4}{1/5} \right\} min{11/58,1/54}。故 x 3 x_3 x3 是离基变量,新的单纯形表2.4,由于 r N = ( 3 11 , 6 11 ) ≥ 0 r_N=(\frac{3}{11},\frac{6}{11})\ge 0 rN=(113,116)≥0,当前基本可行解 x = ( 36 11 , 40 11 , 0 , 0 , 75 11 ) T x=(\frac{36}{11},\frac{40}{11},0,0,\frac{75}{11})^T x=(1136,1140,0,0,1175)T 是线性规划的最优解,最优值为 − 30 2 11 -30\frac{2}{11} −30112。
在上述单纯形算法中,我们要求问题有一个初始基本可行解,下面讨论如何在一般情况下求问题的初始可行解。考虑标准形式的线性规划:
( L P ) min { c T x ∣ A x = b , x ≥ 0 } (LP)\quad \min\{c^{\text{T}}x|Ax = b,x\ge 0\} (LP)min{cTx∣Ax=b,x≥0}
这里 b ≥ 0 b\ge 0 b≥0,引入人工变量 y ∈ R + m y\in \R^{m}_+ y∈R+m,考虑如下线性规划:
( L P a ) min { e T y ∣ A x + y = b , x ≥ 0 , y ≥ 0 } (LP^a)\quad \min\{e^{\text{T}}y|Ax+y = b,x\ge 0,y\ge 0\} (LPa)min{eTy∣Ax+y=b,x≥0,y≥0}
下列结论显然成立:
- 线性规划( L P a LP^a LPa)可行且有可行解 ( x , y ) = ( 0 , b ) (x,y)=(0,b) (x,y)=(0,b),其最优值大于或等于0.
- 线性规划 ( L P ) (LP) (LP)有可行解当且仅当 ( L P a ) (LP^a) (LPa)的最优值为0。特别地,若 ( L P a ) (LP^a) (LPa)的最优解中人工变量 y i ( i = 1 , . . . , m ) y_i(i=1,...,m) yi(i=1,...,m) 都是非基变量,则该最优解也是 ( L P ) (LP) (LP) 的一个基本可行解
利用上述方法求初始基本可行解称为阶段Ⅰ,而获得初始可行解后求解原问题的最优解成为阶段Ⅱ。整个求解过程称为两阶段方法。
例2.1(续):用阶段Ⅰ求解初始可行解,可以构造如下问题:
min y 1 + y 2 + y 3 , s . t . − x 1 + 2 x 2 + x 3 + y 1 = 4 , 5 x 1 + x 2 + x 4 + y 2 = 20 , 2 x 1 + 2 x 2 − x 5 + y 3 = 7 , x ≥ 0 , y ≥ 0 \begin{aligned} &\min y_1+y_2+y_3,\\ &s.t.-x_1+2x_2+x_3+y_1=4,\\ &\quad\quad 5x_1+x_2+x_4+y_2=20,\\ &\quad\quad 2x_1+2x_2-x_5+y_3=7,\\ &\quad\quad x\ge 0,y\ge 0 \end{aligned} miny1+y2+y3,s.t.−x1+2x2+x3+y1=4,5x1+x2+x4+y2=20,2x1+2x2−x5+y3=7,x≥0,y≥0
注意到 x 3 x_3 x3 和 x 4 x_4 x4 可以看作是松弛变量,故人工变量 y 1 y_1 y1 和 y 2 y_2 y2 是多余的,只需引进 y 3 y_3 y3 为人工变量。故阶段Ⅰ的线性规划问题可简化为:
min y 3 , s . t . − x 1 + 2 x 2 + x 3 = 4 , 5 x 1 + x 2 + x 4 = 20 , 2 x 1 + 2 x 2 − x 5 + y 3 = 7 , x ≥ 0 , y 3 ≥ 0 \begin{aligned} &\min y_3,\\ &s.t.-x_1+2x_2+x_3=4,\\ &\quad\quad 5x_1+x_2+x_4=20,\\ &\quad\quad 2x_1+2x_2-x_5+y_3=7,\\ &\quad\quad x\ge 0,y_3\ge 0 \end{aligned} miny3,s.t.−x1+2x2+x3=4,5x1+x2+x4=20,2x1+2x2−x5+y3=7,x≥0,y3≥0
显然,初始基变量为 x B = ( x 3 , x 4 , y 3 ) T x_B=(x_3,x_4,y_3)^T xB=(x3,x4,y3)T,对应的单纯形表见表2.5。选择 x 1 x_1 x1 进基, λ = min ( 20 5 , 7 2 ) \lambda=\min(\frac{20}{5},\frac{7}{2}) λ=min(520,27),故 y 3 y_3 y3 出基,新的基变量为 x B = ( x 1 , x 3 , y 4 ) T x_B=(x_1,x_3,y_4)^T xB=(x1,x3,y4)T,对应的单纯形表见表2.6。这就得到初始基本可行解 x = ( 7 2 , 0 , 15 2 , 5 2 , 0 ) T x=(\frac{7}{2},0,\frac{15}{2},\frac{5}{2},0)^T x=(27,0,215,25,0)T。在单纯形表2.6中删除对应的列就得到阶段Ⅱ的初始单纯形表
2.3 线性规划对偶与对偶单纯形法
考虑下列线性规划问题:
( P ) max { c T x ∣ A x ≤ b , x ∈ R + n } (\text{P})\quad \max\{c^{\text{T}} x|Ax\le b,x\in \R^n_{+}\} (P)max{cTx∣Ax≤b,x∈R+n}
此处 A ∈ R m × n A\in \R^{m\times n} A∈Rm×n, A A A 行满秩,§ 的对偶问题定义为:
( D ) min { b T u ∣ A T u ≥ c , u ∈ R + m } (\text{D})\quad \min\{b^{\text{T}} u|A^{\text{T}}u\ge c,u\in \R^m_{+}\} (D)min{bTu∣ATu≥c,u∈R+m}
这里 R + m R^m_{+} R+m 表示 m m m 维非负向量集合。容易验证,标准形式的线性规划
( LP ) min { c T x ∣ A x = b , x ∈ R + n } (\text{LP})\quad \min\{c^{\text{T}} x|Ax= b,x\in \R^n_{+}\} (LP)min{cTx∣Ax=b,x∈R+n}
的对偶问题为:
( LD ) max { b T u ∣ A T u ≤ c , u ∈ R + m } (\text{LD})\quad \max\{b^{\text{T}} u|A^{\text{T}}u\le c,u\in \R^m_{+}\} (LD)max{bTu∣ATu≤c,u∈R+m}
定理2.9 (弱对偶性) 设 x x x 是 (LP) 的可行解, u u u 是 (LD) 的可行解,则 c T x ≥ b T u c^{\text{T}} x\ge b^{\text{T}} u cTx≥bTu
推论2.1 若 v ( L P ) = − ∞ v(LP)=-∞ v(LP)=−∞,则(LD)不可行;反之若 v ( L D ) = + ∞ v(LD)=+∞ v(LD)=+∞,则(LP)不可行。即当原始线性规划问题(LP)是无界的,对偶问题(LD)一定不可行。
推论2.2 (互补松弛条件)设 x x x 和 u u u 分别是(LP)和(LD)的可行解,令 s = c − A T u s=c-A^{\text{T}}u s=c−ATu,则 x x x 和 u u u 分别是(LP)和(LD)的最优解的充要条件是 s i x i = 0 , i = 1 , . . . , n s_ix_i=0,i=1,...,n sixi=0,i=1,...,n。
定理2.10 (强对偶性)设(LP)或(LD)可行且最优解有限,则 v ( L P ) = v ( L D ) v(LP)=v(LD) v(LP)=v(LD)。
即如果原始问题(LP)和对偶问题(LD)中至少存在一个可行解,并且两个问题都有有限的最优解,那么它们的最优目标函数值是相等的
推论2.3 对线性规划(LP)和它的对偶问题(LD),只有下面四种情况之一发生:
- (LP)和(LD)都有有限最优解且 v ( L P ) = v ( L D ) v(LP)=v(LD) v(LP)=v(LD);
- v ( L P ) = − ∞ v(LP)=-∞ v(LP)=−∞,(LD)不可行;
- v ( L D ) = + ∞ v(LD)=+∞ v(LD)=+∞,(LP)不可行;
- (LP)和(LD)皆不可行.
推论2.4 (Farkas引理) 设 A ∈ R m × n , c ∈ R n A\in \R^{m\times n},c\in \R^n A∈Rm×n,c∈Rn,则下列系统有且仅有一个有解:
- A x ≤ 0 , c T x > 0 Ax\le 0,c^Tx>0 Ax≤0,cTx>0
- A T u = c , u ≥ 0 A^Tu=c,u\ge0 ATu=c,u≥0
性质2.2 设 A = ( B , N ) A=(B,N) A=(B,N), B B B 是(LP)的对偶可行基,即 r N = c N T − c B T B − 1 N ≥ 0 r_N=c_N^T-c_B^TB^{-1}N\ge0 rN=cNT−cBTB−1N≥0,令 B \mathcal{B} B 和 N \mathcal{N} N 分别表示 B B B 和 N N N 的列指标集,记 a ‾ j = B − 1 a j , j ∈ N , b ‾ = B − 1 b \overline{a}_j=B^{-1}a_j,j\in \mathcal{N},\overline{b}=B^{-1}b aj=B−1aj,j∈N,b=B−1b,设 b ‾ s < 0 \overline{b}_s<0 bs<0
- 若 a ‾ s j ≥ 0 , ∀ j ∈ N \overline{a}_{sj}\ge 0,\forall j\in \mathcal{N} asj≥0,∀j∈N,则(LP)不可行
- 若存在 j ∈ N j\in \mathcal{N} j∈N 使 a ‾ s j < 0 \overline{a}_{sj}<0 asj<0,则有 B B B 的邻接对偶可行基 B ‾ \overline{B} B,其列指标集 B ‾ = B ∪ { t } ∪ { s } \overline{\mathcal{B}}=\mathcal{B}\cup\{t\}\cup\{s\} B=B∪{t}∪{s},这里
t = arg min j ∈ N { − r j a ‾ s j ∣ a ‾ s j < 0 } (2.14) t=\arg\underset{j\in \mathcal{N}}{\min}\{ -\cfrac{r_j}{\overline{a}_{sj}}|\overline{a}_{sj}<0\}\tag{2.14} t=argj∈Nmin{−asjrj∣asj<0}(2.14)
对偶单纯形算法
- 步0 计算初始对偶可行基 B B B, A = ( B , N ) A=(B,N) A=(B,N)
- 步1 如果 b ‾ = B − 1 b ≥ 0 \overline{b}=B^{-1}b\ge 0 b=B−1b≥0,则 x T = ( x B T , 0 ) = ( b ‾ T , 0 ) ≥ 0 x^T=(x_B^T,0)=(\overline{b}^T,0)\ge 0 xT=(xBT,0)=(bT,0)≥0是原问题的最优解,否则,转步2
- 步2 选择 s s s 满足 b ‾ s < 0 \overline{b}_s<0 bs<0,若 a ‾ s j ≥ 0 , ∀ j ∈ N \overline{a}_{sj}\ge 0,\forall j\in \mathcal{N} asj≥0,∀j∈N,则原问题不可行,否则由(2.14)可得 t t t,令 B : = B ∪ { t } ∪ { s } {\mathcal{B}}:=\mathcal{B}\cup\{t\}\cup\{s\} B:=B∪{t}∪{s},转到步1
例2.1(续)线性规划可写为
min − 7 x 1 − 2 x 2 s . t . − x 1 + 2 x 2 + x 3 = 4 , 5 x 1 + x 2 + x 4 = 20 , 2 x 1 + 2 x 2 − x 5 = 7 , x ≥ 0 \begin{aligned} &\min -7x_1-2x_2\\ &s.t.-x_1+2x_2+x_3=4,\\ &\quad\quad 5x_1+x_2+x_4=20,\\ &\quad\quad 2x_1+2x_2-x_5=7,\\ &\quad\quad x\ge 0 \end{aligned} min−7x1−2x2s.t.−x1+2x2+x3=4,5x1+x2+x4=20,2x1+2x2−x5=7,x≥0
使用对偶单纯形法求解:
第1次迭代.选择初始可行基为 B = ( a 2 , a 3 , a 5 ) B=(a_2,a_3,a_5) B=(a2,a3,a5) .对应的单纯形表为表2.7.因 r N = r N = c N T − c B T B − 1 N = ( 3 , 2 ) ≥ 0 r_N=r_N=c_N^T-c_B^TB^{-1}N=(3,2)≥0 rN=rN=cNT−cBTB−1N=(3,2)≥0,故 B = ( a 2 , a 3 , a 5 ) B=(a_2,a_3,a_5) B=(a2,a3,a5) 是对偶可行基。而 x B = b ‾ = ( − 36 , 20 , 33 ) T x_B=\overline{b}=(-36,20,33)^T xB=b=(−36,20,33)T,故 B B B 不是原始可行基。
第二次迭代,选择 b ‾ 3 = − 36 < 0 \overline{b}_3=-36<0 b3=−36<0,计算 λ = min ( 3 11 , 3 2 ) = 3 11 \lambda =\min(\cfrac{3}{11},\cfrac{3}{2})=\cfrac{3}{11} λ=min(113,23)=113,所以 x 1 x_1 x1 进基, x 3 x_3 x3 离基,新的对偶可行基为 B = ( a 1 , a 2 , a 5 ) B=(a_1,a_2,a_5) B=(a1,a2,a5),对应的单纯形表如下。此时对偶可行解为 x = ( 36 11 , 40 11 , 0 , 0 , 75 11 ) x=(\cfrac{36}{11},\cfrac{40}{11},0,0,\cfrac{75}{11}) x=(1136,1140,0,0,1175) 也是原始可行解,从而是原始最优解。
参考文献
- 整数规划 孙小玲,李瑞 北京,科学出版社 2010
- 凸集
- 运筹学S01E02——单纯形法
- 简单理解线性规划的单纯形算法