问题引入
1275. 最大数
给定一个正整数数列 a1,a2,…,an,每一个数都在 0∼p−1 之间。
可以对这列数进行两种操作:
- 添加操作:向序列后添加一个数,序列长度变成 n+1;
- 询问操作:询问这个序列中最后 L 个数中最大的数是多少。
程序运行的最开始,整数序列为空。
一共要对整数序列进行 m 次操作。
写一个程序,读入操作的序列,并输出询问操作的答案。
输入格式
第一行有两个正整数 m,p,意义如题目描述;
接下来 m 行,每一行表示一个操作。
如果该行的内容是 Q L,则表示这个操作是询问序列中最后 L 个数的最大数是多少;
如果是 A t,则表示向序列后面加一个数,加入的数是 (t+a) mod p。其中,t 是输入的参数,a 是在这个添加操作之前最后一个询问操作的答案(如果之前没有询问操作,则 a=0)。
第一个操作一定是添加操作。对于询问操作,L>0�>0 且不超过当前序列的长度。
输出格式
对于每一个询问操作,输出一行。该行只有一个数,即序列中最后 L� 个数的最大数。
数据范围
1≤m≤2×105,
1≤p≤2×109,
0≤t
输入样例:
10 100
A 97
Q 1
Q 1
A 17
Q 2
A 63
Q 1
Q 1
Q 3
A 99
输出样例:
97
97
97
60
60
97
样例解释
最后的序列是 97,14,60,96。
这种题大家一看就知道打暴力,但是一看数据范围就知道只能得部分分。
纯暴力代码如下:
#include
using namespace std;
const int N = 1e5 + 10;
int a[N];
int m, p;
int main() {
int cnt = 0;
cin >> m >> p;
int f = 0;
for(int i = 1; i <= m; i++) {
char k;
cin >> k;
if(k == 'Q') {
int l;
cin >> l;
int maxn = -1;
for(int j = cnt; j >= cnt - l + 1; j--) {
maxn = max(a[j], maxn);
}
cout << maxn << endl;
f = maxn;
}
else {
int l;
cin >> l;
int kk = (l + f) % p;
a[++cnt] = kk;
}
}
//for(int i = 1; i <= cnt; i++) cout << a[i] << " ";
}
我们之前学过的前缀和算法可以解决区间求和的问题,并且时间复杂度是O(1),但如果涉及到修改操作,前缀和数组都需要重新计算,时间复杂度也是O(n).
那么有没有什么东西能兼顾两者呢?这就是我们要学习的线段树!把修改和查询的时间复杂度都降到O(logn)!!!
算法思想
先来看一下线段树是什么东西!!!
有以下数组(为方便计算,数组下标从1开始)
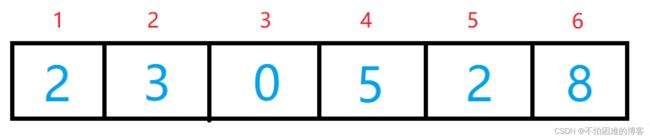
我们把它转换成线段树,是长这样的:
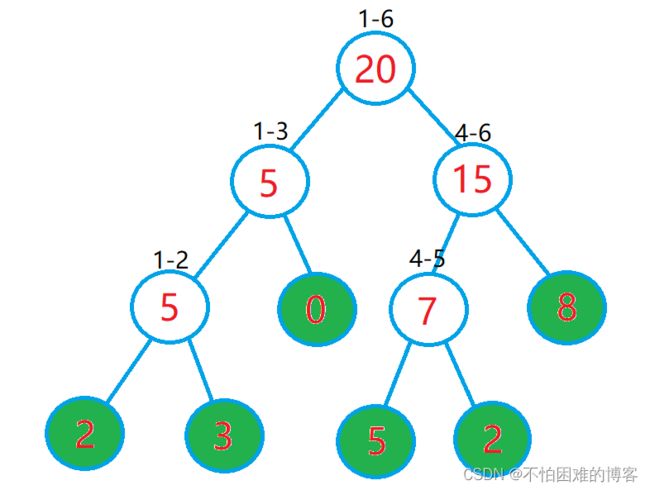
(1)叶子结点(绿色)存的都是原数组元素的值
(2)每个父结点(sum)是它的两个子节点的值的和
(3)每个父结点记录它表示区间的范围,如上图的“4-5”表示4到5的区间
下面我们看看线段树是如何实现查询和修改操作(和懒标记)的,顺便看看他是如何降低了时间复杂度的。
查询操作
例如我们需要查询2-5区间的和
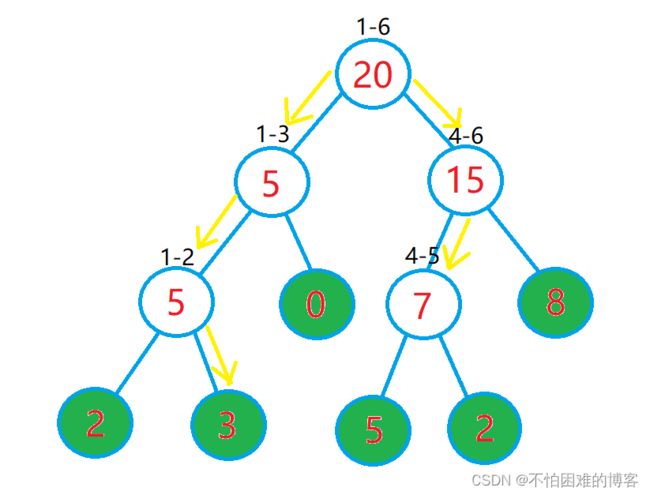
使用递归的思想:
2~5的和
=2~3的和+4~5的和
=3+0+4~5的和
=3+0+7
=10
总之,就是把查询的区间细化成几个区间的和,在把细化的区间和算出来就行了。
修改操作
例如,我们要把结点6的值由8->7,线段树需要沿着黄色部分一个一个改,直到根结点:
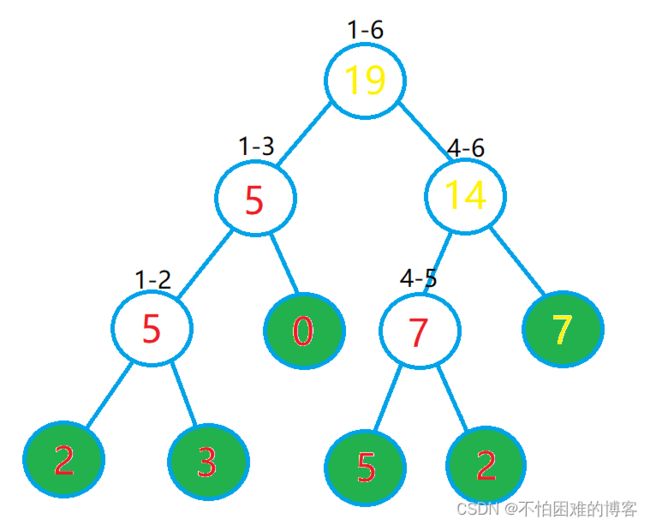
不管是修改操作还是查询操作,时间复杂度都是O(logn),可见线段树的厉害!!!
下一步我们来看如何实现线段树!
算法实现
首先我们需要将原始数组建立成一棵线段树,然后在树的基础上支持区间查询,区间和单点修改的操作。
建树
观察上图,我们发现线段树是一棵近似就是完全二叉树,利用完全二叉树的性质,我们就可以直接用一个数组来存它。
代码如下:
#include
using namespace std;
const int N = 1e4;
struct node {
int l, r, sum;
};
node tree[N * 4 + 10];
int a[N + 10];
void build(int x, int l, int r) {
tree[x] = {l, r};//也可以写成tree[x].l = l, tree[x].r = r;
//初始化每个节点的左右边界
printf("%d:%d %d\n", x, l, r);
if(l == r) {
tree[x].sum = a[l];//只有叶子节点是真正赋值的,其他节点都要进行pushup操作
return;
}
int mid = l + r >> 1;
//递归左右儿子节点
build(x << 1, l, mid);
build(x << 1 | 1, mid + 1, r);
//递归完成后,进行pushup操作
tree[x].sum = tree[x * 2].sum + tree[x * 2 + 1].sum;
}
int main() {
int n;
cin >> n;
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
printf("运行结果如下:\n");
build(1, 1, n);
for(int i = 1; i <= n; i++) {
if(n * 2 <= pow(2, i) - 1) {
n = i;
break;
}
}
for(int i = 1; i <= pow(2, n) - 1; i++) {
printf("tree[%d].sum = %d\n", i, tree[i].sum);
}
printf("在完全二叉树中,0表示这个空间没有数,但是占空间\n");
}
运行效果如下:
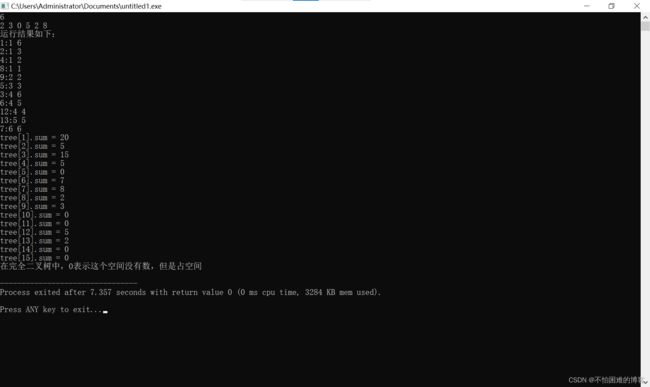
区间查询
区间查询就是把查询的区间细化成几个区间的和,在把细化的区间和算出来就行了(当然不仅仅局限与求和,求最大值等等也可以实现,改个符号就行了)。
这里以求和为例。
代码如下:
#include
using namespace std;
const int N = 1e4;
struct node {
int l, r, sum;
};
node tree[N * 4 + 10];
int a[N + 10];
void build(int x, int l, int r) {
tree[x] = {l, r};//也可以写成tree[x].l = l, tree[x].r = r;
//初始化每个节点的左右边界
//printf("%d:%d %d\n", x, l, r);
if(l == r) {
tree[x].sum = a[l];//只有叶子节点是真正赋值的,其他节点都要进行pushup操作
return;
}
int mid = l + r >> 1;
//递归左右儿子节点
build(x << 1, l, mid);
build(x << 1 | 1, mid + 1, r);
//递归完成后,进行pushup操作
tree[x].sum = tree[x * 2].sum + tree[x * 2 + 1].sum;
}
int query(int x, int l, int r) {
//区间查询
if(tree[x].l >= l && tree[x].r <= r) return tree[x].sum;//如果该节点的区间被要查找的区间包括了,那么就不用继续找了,直接返回改节点的值就行了
int mid = (tree[x].l + tree[x].r) / 2;
int sum = 0;
if(l <= mid) sum += query(x * 2, l, r);//如果当前节点在要查找区间左边界的右面,那么递归查找左子树
if(r > mid) sum += query(x * 2 + 1, l, r);//如果当前节点在要查找区间右边界的左面,那么递归查找右子树
return sum;//由此得出了该区间的值,返回即可
}
int main() {
int n, m;
cin >> n >> m;//n为有n数,m为有m次询问。
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
build(1, 1, n);
for(int i = 1; i <= m; i++) {
int l, r;
cin >> l >> r;
printf("%d~%d的和为:%lld\n", l, r, query(1, l, r));
}
return 0;
}
运行效果如下:
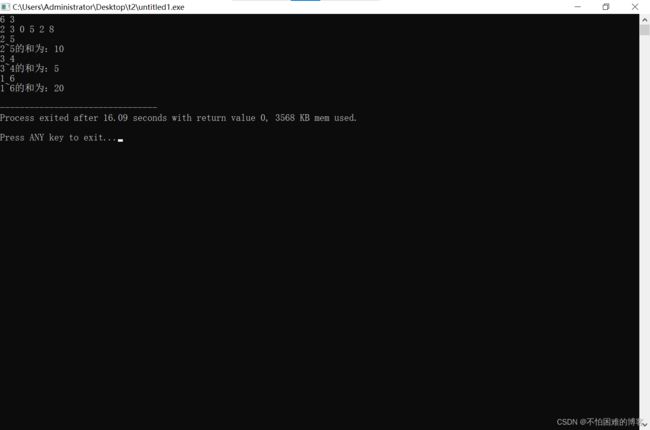
单点修改
单点修改就是先递归找到要修改的数,然后从这个数一直修改,修改到根节点的过程。
代码如下:
#include
using namespace std;
const int N = 1e4;
struct node {
int l, r, sum;
};
node tree[N * 4 + 10];
int a[N + 10];
void build(int x, int l, int r) {
tree[x] = {l, r};//也可以写成tree[x].l = l, tree[x].r = r;
//初始化每个节点的左右边界
//printf("%d:%d %d\n", x, l, r);
if(l == r) {
tree[x].sum = a[l];//只有叶子节点是真正赋值的,其他节点都要进行pushup操作
return;
}
int mid = l + r >> 1;
//递归左右儿子节点
build(x << 1, l, mid);
build(x << 1 | 1, mid + 1, r);
//递归完成后,进行pushup操作
tree[x].sum = tree[x * 2].sum + tree[x * 2 + 1].sum;
}
int query(int x, int l, int r) {
//区间查询
if(tree[x].l >= l && tree[x].r <= r) return tree[x].sum;//如果该节点的区间被要查找的区间包括了,那么就不用继续找了,直接返回改节点的值就行了
int mid = (tree[x].l + tree[x].r) / 2;
int sum = 0;
if(l <= mid) sum += query(x * 2, l, r);//如果当前节点在要查找区间左边界的右面,那么递归查找左子树
if(r > mid) sum += query(x * 2 + 1, l, r);//如果当前节点在要查找区间右边界的左面,那么递归查找右子树
return sum;//由此得出了该区间的值,返回即可
}
void change(int now, int x, int k){//单点修改
if(tree[now].l == tree[now].r) tree[now].sum = k;//如果找到该节点,修改它
else {
//printf("%d:%d %d\n", now, x, k);
int mid = (tree[now].l + tree[now].r) / 2;//等价于<<1,但是加不加没有区别
if(x <= mid) change(now * 2, x, k);
else change(now * 2 + 1, x, k);
tree[now].sum = tree[now * 2].sum + tree[now * 2 + 1].sum;//pushup操作
}
}
int main() {
int n, m;
cin >> n >> m;//n为有n数,m为有m次询问。
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
build(1, 1, n);
printf("原来的数组:");
cout << "\n";
//cout << tree[1].sum << endl;
for(int i = 1; i <= 16; i++) printf("tree[%d].sum = %d\n", i, tree[i].sum);
change(1, 1, 9);
printf("现在的数组:");
//cout << tree[1].sum << endl;
for(int i = 1; i <= 16; i++) printf("tree[%d].sum = %d\n", i, tree[i].sum);
return 0;
}
运行效果如下:
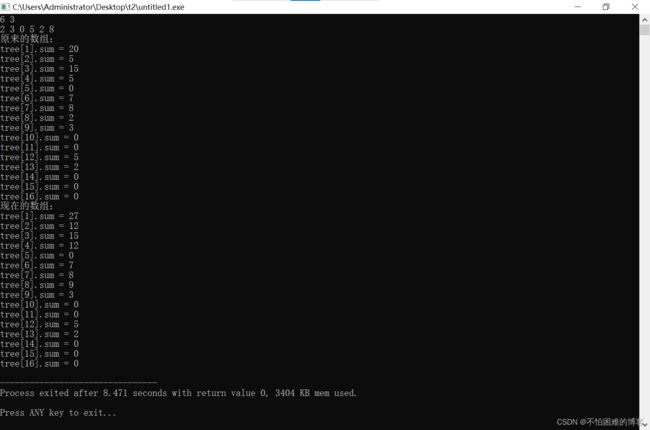
还有懒标记没写,改日更新,敬请期待!!!






