算法练习--leetcode 数组
文章目录
- 爬楼梯问题
- 裴波那契数列
- 两数之和 [数组]
- 合并两个有序数组
- 移动零
- 找到所有数组中消失的数字
- 三数之和
爬楼梯问题
输入n阶楼梯,每次爬1或者2个台阶,有多少种方法可以爬到楼顶?
示例1:输入2, 输出2
一次爬2阶;
一次爬1阶;
故两种方法。
示例2:
输入3, 输出3
三个1;
一个1 + 一个 2;
一个2 + 一个1;
python实现:
# 递归
def climb_stairs(n):
if n == 1:
return 1
elif n == 2:
return 2
elif n >= 3:
return climb_stairs(n-1) + climb_stairs(n-2)
# 递归优化,避免重复计算(优化效果微小)
def climb_stairs_2(n):
d = {}
if n == 1:
return 1
elif n == 2:
return 2
elif n >= 3:
if n in d:
return d.get(n) # 避免一部分递归操作
cur = climb_stairs(n-1) + climb_stairs(n-2)
d[n] = cur
return cur
# 循环一次计算(自底向上依次计算)
# O(n)
def climb_stairs_3(n):
if n == 1:
return 1
elif n == 2:
return 2
elif n >= 3:
a = 1
b = 2
result = 0
for i in range(3, n+1):
result = a + b
a = b
b = result
return result
java实现:
// O(n)
class Solution{
public int climbStairs(int n){
if(n == 1) return 1;
else if(n == 2) return 2;
else if(n >= 3){
int result = 0;
int a = 1;
int b = 2;
for(int i=3; i<=n; i++){
result = a + b;
a = b;
b = result;
}
return result;
}
}
}
裴波那契数列
两数之和 [数组]
给定一个整数数组 nums 和一个整数目标值 target,在该数组中找出 和 等于目标值 target 的那两个整数,并返回它们的数组下标。
假设每种输入只会对应一个答案,且数组中同一个【位置】的元素在答案里不能重复出现。
示例 1:
输入:nums = [2,7,11,15], target = 9
输出:[0,1]
解释:因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入:nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入:nums = [3,3], target = 6
输出:[0,1]
暴力解法:
- 依次遍历元素,计算求和,并比较。
- 时间复杂度 O ( n 2 ) {O(n^2)} O(n2)
- python实现
# O(n^2)
def calcSum(arr, target):
n = len(arr)
for i in range(n-1):
for j in range(i+1, n):
if arr[i] + arr[j] == target:
return [i, j]
raise ValueError("未找到结果")
- java实现
在这里插入代码片
哈希优化
- 遍历数组,索引为 i;
- 判断 left = target - array[i] ,left 值是否存在于hash;
- 存在,则返回索引 i 和 hash中left 对应的值;
- 不存在,则将 array[i] :i 存入hash;
- 时间复杂度 O ( n ) {O(n)} O(n)
- python实现
# python
def optimize_calc_sum(alist, target):
dict_ = {}
n = len(alist)
for i in range(n):
if target - alist[i] in dict_:
return [i, dict_.get(target - alist[i])]
dict_[alist[i]] = i
raise ValueError("未找到结果")
- java实现
在这里插入代码片
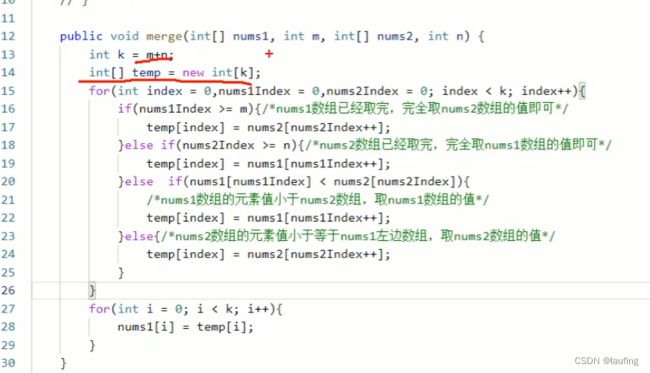
合并两个有序数组
给两个非递减排列的整数数组arr1、arr2,m 和 n 分别表示arr1 、arr2的元素个数;合并arr2到arr1中,合并后元素非递减排列。
示例1:
arr1 = [1, 2, 3, 0, 0, 0] m = 3
arr2 = [2, 5, 6] n = 3
合并结果:[1,2,2,3,5,6] 黑体数字为arr2中的元素
示例2:
arr1 = [1]
arr2 = [ ]
合并结果: [1]
python实现:
arr1 = [1, 3, 4, 0, 0, 0]
m = 3
arr2 = [2, 5, 6]
n = 3
def merge_array(arr1, m, arr2, n):
# 准备临时数组
temp = [] # 空间复杂度O(m+n)
i = 0
j = 0
while i < m and j < n: # O(m+n) 线性复杂度
if arr1[i] <= arr2[j]:
temp.append(arr1[i])
i += 1
else:
temp.append(arr2[j])
j += 1
if i == m:
temp.extend(arr2[j:n])
elif j == n:
temp.extend(arr1[i:m])
for i in range(m + n):
arr1[i] = temp[i]
print("arr1:", arr1)
return arr1
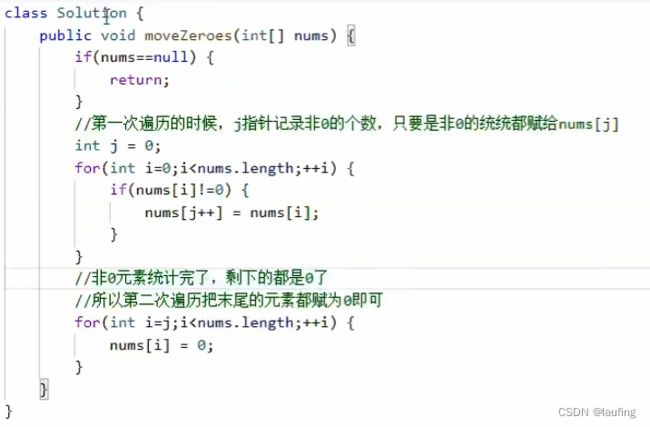
移动零
给定一个数组array,将内部所有的0移动到数组的末尾,并保持非零元素的相对顺序。必须原位操作,不能拷贝额外的数组。
示例:
输入,[0, 1, 0, 3, 12]
输出,[1, 3, 12, 0, 0]
提示:双指针
python实现:
# 暴力实现
arr = [0, 1, 0, 3, 12, 0, 0, 13, 0, 14, 0, 18, 0, 0, 0]
# 依次将遍历的首个0值与后面的非0置换
def move_zero(arr):
n = len(arr)
for i in range(n):
if arr[i] != 0:
continue
k = i # 记录当前0的位置
j = i + 1 # 下一个元素的位置
while j < n:
if arr[j] == 0:
j += 1
continue
arr[k], arr[j] = arr[j], arr[k]
k = j
j += 1
print("result:", arr)
return arr
# 双指针
# 双指针同时从0开始
# 依次将后一个指针的非0值,放到前一个指针的位置,前一个指针+1,继续下次循环
# 最后将后一个指针处到结束 均赋值0
# 时间复杂度 O(2n)
def move_zero_double_pointer(arr):
n = len(arr)
j = 0 # j指针
for i in range(n): # i指针 两个指针同时从0开始
if arr[i] != 0:
arr[j] = arr[i]
j += 1
# 将从j开始的元素 全部赋值0
while j < n: # 时间复杂度 O(2n)
arr[j] = 0
j += 1
print("result:", arr)
return arr
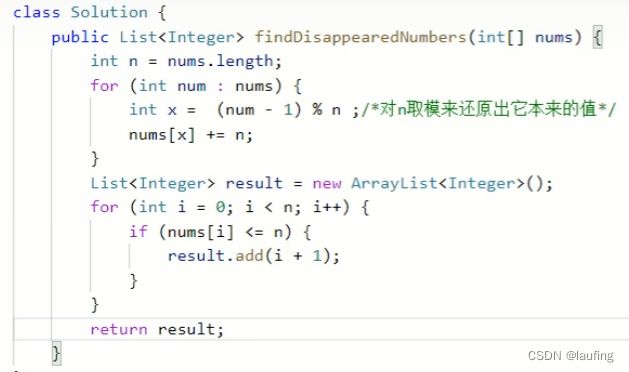
找到所有数组中消失的数字
给定一个n个整数的数组array,每个元素值在【1,n】之间,找出1-n内没有出现在array中的数字,以数组形式返回。
n为数组的长度;
示例1:
输入:[4,3,2,7,8,2,3,1]
输出:[5,6]
示例2:
输入:[1,1]
输出:[2]
进阶:可以不借助额外空间且时间复杂度为O(n),解决吗?
python实现:
# 暴力实现
def find_missing_digit(arr):
n = len(arr) # [1, ..., n]
# arr去重
temp = [] # 空间复杂度O(n)
for i in range(1, n+1): # 时间复杂度 O(n)
if i not in arr:
temp.append(i)
print("result:", temp)
return temp
# 优化空间复杂度O(1)
# 只能依赖数组本身的空间
# 所有元素的值 - 1 可以对应索引,对应索引处的值 都+n 或者2n....
# 而缺失的那些值 - 1 对应的索引处的值肯定没有变化,即 <= n
# 最后循环找到<=n的元素,其索引+1 就是缺失的值
def optimize_find_missing_digit(arr):
n = len(arr)
# 空间复杂度为O(1) 只能使用数组本身的空间
for i in arr:
idx = (i - 1) % n # 得到对应的索引(拿到的i可能是已改过的) 所以需要还原索引
arr[idx] += 2 * n
temp = [] # 存储最终结果的空间不算 额外空间
for i in range(n):
if arr[i] <= n:
temp.append(i + 1)
print("result:", temp)
return temp
三数之和
给一个整数数组 nums ,判断是否存在三元组 [ nums[i], nums[j], nums[k] ] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。返回所有和为 0 且不重复的三元组,如果三个元素只是顺序不同,则算重复的三元组。
示例 1:
输入:[-1,0,1,2,-1,-4]
输出:[[-1,-1,2],[-1,0,1]]
解释:
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意,输出的顺序和三元组的顺序并不重要。
示例 2:
输入:[0,1,1]
输出:[]
解释:唯一可能的三元组和不为 0 。
示例 3:
输入:[0,0,0]
输出:[[0,0,0]]
解释:唯一可能的三元组和为 0 。
提示:
3 <= nums.length <= 3000
-105 <= nums[i] <= 105
python实现:
# 暴力解法 O(n^3) 会产生重复的三元组
arr = [-1,0,1,2,-1,-4]
def three_nums_sum(arr: List[int]) -> List[List[int]]:
n = len(arr)
temp = []
for i in range(n-2):
for j in range(i+1, n-1):
for k in range(j+1, n):
if arr[i] + arr[j] + arr[k] == 0:
temp.append([arr[i], arr[j], arr[k]])
# result: [[-1, 0, 1], [-1, 2, -1], [0, 1, -1]]
# 会产生重复的三元组
print("result:", temp)
return temp
# 排序 + 双指针
# 时间复杂度 O(n^2)
def optimize_three_nums_sum(nums: List[int]) -> List[List[int]]:
n = len(nums)
res = []
if n < 3:
return []
nums.sort() # 排序 快排 O(nlogn)
res = []
for i in range(n): O(n^2)
if (nums[i] > 0):
return res
if (i > 0 and nums[i] == nums[i - 1]): # 防止重复解
continue
# 双指针
L = i + 1
R = n - 1
while (L < R):
if (nums[i] + nums[L] + nums[R] == 0):
res.append([nums[i], nums[L], nums[R]])
# 去除重复
while (L < R and nums[L] == nums[L + 1]):
L = L + 1
while (L < R and nums[R] == nums[R - 1]):
R = R - 1
L = L + 1
R = R - 1
elif (nums[i] + nums[L] + nums[R] > 0):
R = R - 1
else:
L = L + 1
return res
java实现:
pass
[下一篇]:算法练习–leetcode 链表