【数据结构】手把手带你搞懂顺序表(带图详解)
文章目录
- 前言
- 1、顺序表
-
- 1.1、顺序表的结构体
- 1.2、功能实现
-
- 初始顺序表
- 增加顺序表长度
- 顺序表的查找
- 顺序表的插入
- 顺序表的删除
- 打印顺序表
- 顺序表的销毁
- 1.3 顺序存储结构的优缺点
- 顺序表总代码
前言
在本篇博客中,我会概述顺序表、讲解链表的概念和结构分类、以及使用C语言实现单链表。话不多说,我们这就开始。
1、顺序表
数据结构分为线性表和非线性表,今天我们要学习的顺序表就是线性表中的一个小类。那么,何为线性表,线性表是指n个具有相同性质的数据元素的有限序列,常见的线性表有:顺序表、链表、栈、队列、字符串等等。
注意,线性表的物理结构不一定是线性的,它在逻辑结构上一定是线的。
顺序表(SeqList):顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构(连续存储数据,不能跳跃)。
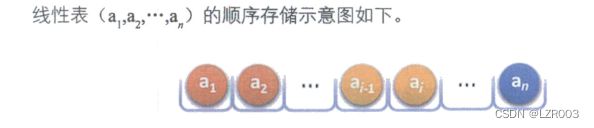
1.1、顺序表的结构体
顺序表可以采用的两中方式,一种是静态结构,另一中动态结构(动态结构更优)。
#pragma once
#include 1.2、功能实现
具有以下几种功能要求:
//顺序表初始化
void SeqListInit(SeqList* ps); //psl p指针,sl顺序表
//检查空间,如果满了,进行扩容
void SeqListCheckCapacity(SeqList* ps);
//顺序表查找
int SeqListFind(SeqList* ps, SLDateType x);
//顺序表在pos位置插入x
void SeqListInsert(SeqList* ps, int pos,SLDateType x);
//顺序表删除pos位置的值
void SeqListErase(SeqList* ps, int pos);
//顺序表销毁
void SeqListDestory(SeqList* ps);
//打印顺序表
void PrintSL(SeqList* ps);
初始顺序表
首先得进行初始化,初始化时可以先给一点空间,也可以不给空间(因为空间满了会进行扩容)
void SeqListInit(SeqList* ps) {
ps->size = 0;
ps->capacity = 0;
ps->a = NULL;
}
增加顺序表长度
当顺序表内的空间已经满了,这时候我们就需要扩大顺序表的空间以便存储更多的数据。由于静态数组的长度不可以改变,而动态数组可以通过relloc()函数重新申请更大一个空间,然后再把原来空间的数据传输到新的空间里,最后销毁原来的顺序表或者再原空间上扩大(取决于内存情况).
PS:如果还不明白的话可以去看看relloc函数,动态内存管理
void check(SeqList* ps) {
assert(ps);
if (ps->size == ps->capacity)//空间容量等于实际长度就该扩容
{
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;//初始给容量赋值为4
SLDateType* tmp = (SLDateType*)realloc(ps->a, newCapacity * sizeof(SLDateType));//开票空间
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->a = tmp;//tmp的首地址传给指针a
ps->capacity = newCapacity;//更新容量大小
}
}
顺序表的查找
要是实现元素查找,即可以将表中遍历是否有相等元素,有则直接返回表中位置,否则返回-1表示未找到。
int SeqListFind(SeqList* ps, SLDateType x) {
assert(ps);
if (ps->size == 0)return -1;
for (int i = 0; i < ps->size; i++)
{
if (ps->a[i] == x)
return i + 1;
}
return -1;
}
顺序表的插入
我们该如何实现在顺序表中的第i个位置插入新元素e呢?
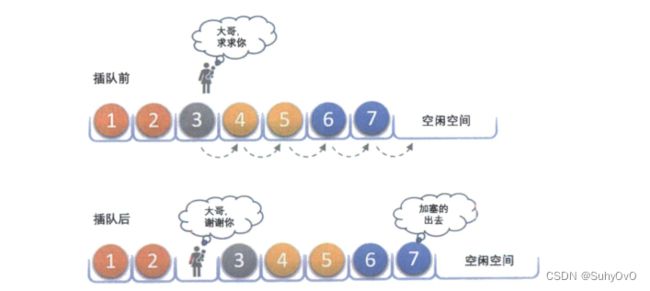
大家可以看到上图就是一个插队的情形,当带娃的母亲查到3号大哥前面,那么3号大哥后面的老铁们都需要往后腾一个位置。
插入算法的思路:
- 首先得判断插入位置是否合理,防止数组越界;
- 若顺序表长度等于空间容量大小,则需要扩容或者抛出异常;
- 从最后一个元素位置开始向前遍历到第i个位置,分别将他们都向后移动一个位置,然后将要插入的元素填入位置i处;
- 表长加1
时间复杂度:O(N);
void SeqListInsert(SeqList* ps, int pos, SLDateType x) {
assert(ps);
if (pos <1 ||pos > ps->size + 1)return;//越界则退出程序
check(ps);//检查空间容量是否满了
for (int i = ps->size - 1; i >= pos - 1; i--) //后移操作
{
ps->a[i + 1] = ps->a[i];
}
ps->a[pos] = x;//将新元素插入
ps->size++;//表长加1
}
顺序表的删除
一群人在排队,有一个女子因骗钱被失主找上赶紧逃走了,那么这个人的位置就空出来了,后面的人就一个个往前一步,补上这个空位。而这过程就相当有顺序表删除元素的过程(如下图)
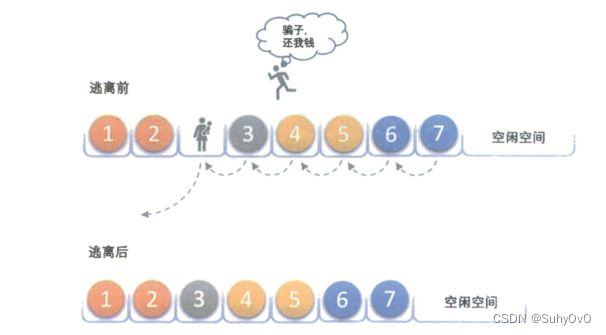
删除算法的思路:
- 首先得判断插入位置是否合理,防止数组越界
- 从删除元素位置开始遍历到最后一个元素位置,将他们都向前移动一个位置
- 表长减1
时间复杂度:O(N);
void SeqListErase(SeqList* ps, int pos) {
assert(ps);
if (pos<1 ||pos>ps->size||ps->size==0)return;//防止越界
for (int i = pos - 1; i < ps->size; i++) //元素前移
{
ps->a[i] = ps->a[i + 1];
}
ps->size--;
}
打印顺序表
void SeqListPrint(SeqList* ps) {
assert(ps);
//这个是判断是否ps为空的,如果为空就强制退出
//相当于这个
/*
if(!ps)return;
*/
if (ps->size == 0) {
cout << "空表" << endl;
return;
}
for (int i = 0; i < ps->size; i++) {
cout << ps->a[i] << " ";
}
cout << endl;
}
顺序表的销毁
顺序表初始化的时候是用malloc函数向系统申请的空间,malloc函数申请的空间是在内存的堆区,堆区的空间不会被系统自动回收,只把size改为0是不够的,还需要用free函数释放空间。
void SeqListDestroy(SeqList* ps)
{
assert(ps);
if (ps) {
free(ps->a);//释放空间
ps->a = NULL;
ps->capacity = ps->size = 0;
}
}
1.3 顺序存储结构的优缺点
线性表的顺序存储结构,在读数据时,不管是哪个位置,时间复杂度都是O(1);而插入或删除时,时间复杂度都是O(n)。这就说明,它比较适合元素个数不太变化,而更多是存取数据的应用。当然,它的优缺点还不只这些……
优点:
- 无须为表示表中元素之间的逻辑关系而增加额外的存储空间可以快速地存取表中任一位置的元素;
- 可以快速地存取表中任意位置的元素;
缺点:
- 插入和删除操作需要移动大量元素 ;
- 当线性表长度变化较大时,难以确定存储空间的容量 ;
- 造成存储空间的“碎片";
顺序表总代码
void SeqListInit(SeqList* ps) {
ps->size = 0;
ps->capacity = 0;
ps->a = NULL;
}
void check(SeqList* ps) {
assert(ps);
if (ps->size == ps->capacity)
{
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
SLDateType* tmp = (SLDateType*)realloc(ps->a, newCapacity * sizeof(SLDateType));
if (tmp == NULL)
{
perror("realloc fail");
exit(-1);
}
ps->a = tmp;
ps->capacity = newCapacity;
}
}
void SeqListDestroy(SeqList* ps)
{
assert(ps);
if (ps) {
free(ps->a);
ps->a = NULL;
ps->capacity = ps->size = 0;
}
}
void SeqListPrint(SeqList* ps) {
assert(ps);
if (ps->size == 0) {
cout << "ձ" << endl;
return;
}
for (int i = 0; i < ps->size; i++) {
cout << ps->a[i] << " ";
}
cout << endl;
}
void SeqListPushBack(SeqList* ps, SLDateType x) {
assert(ps);
check(ps);
ps->a[ps->size] = x;
ps->size++;
}
void SeqListPushFront(SeqList* ps, SLDateType x) {
assert(ps);
check(ps);
for (int i = ps->size - 1; i >= 0; i--)
ps->a[i + 1] = ps->a[i];
ps->a[0] = x;
ps->size++;
}
void SeqListPopFront(SeqList* ps) {
assert(ps);
if (ps->size == 0)return;
for (int i = 0; i < ps->size; i++)
ps->a[i] = ps->a[i + 1];
ps->size--;
}
void SeqListPopBack(SeqList* ps) {
assert(ps);
if (ps->size == 0)return;
ps->size--;
}
int SeqListFind(SeqList* ps, SLDateType x) {
assert(ps);
if (ps->size == 0)return -1;
for (int i = 0; i < ps->size; i++) {
if (ps->a[i] == x) return i + 1;
}
return -1;
}
void SeqListInsert(SeqList* ps, int pos, SLDateType x) {
assert(ps);
if (pos <1 ||pos > ps->size + 1)return;
check(ps);
for (int i = ps->size - 1; i >= pos - 1; i--) {
ps->a[i + 1] = ps->a[i];
}
ps->a[pos] = x;
ps->size++;
}
void SeqListErase(SeqList* ps, int pos) {
assert(ps);
if (pos<1 ||pos>ps->size||ps->size==0)return;
for (int i = pos - 1; i < ps->size; i++) {
ps->a[i] = ps->a[i + 1];
}
ps->size--;
}