算法通关村—轻松搞定二叉树的高度和深度问题

1.二叉树的最大深度

二叉树的最大深度
给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

1.1 递归

通过上面的步骤能够看出，深度取决于左右子树，只要左子树有，那么高度就+1，或者有右子树，只需要将左右子树的高度算出来，然后比较高度再+1即可。

public int maxDepth(TreeNode root) {
        if(root==null) return 0;
        int leftHight = maxDepth(root.left);
        int rightHight = maxDepth(root.right);
        return Math.max(leftHight,rightHight)+1;
    }

1.2 层序遍历

相对简单，只需要每次遍历的时候，结果加1就可以，总体上还是层序遍历操作。

public int maxDepth(TreeNode root) {
        if(root==null) return 0;
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        // 计算深度
        int res =0 ;
        while(!queue.isEmpty()){
            // 每一层的元素数
            int size = queue.size();
            while(size>0){
                TreeNode node = queue.poll();
                if(node.left!=null){
                    queue.offer(node.left);
                }
                if(node.right!=null){
                    queue.offer(node.right);
                }
                size--;
            }
            res++;
        }
        return res;
    }

2. 平衡二叉树

平衡二叉树
给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

2.1 自顶向下递归

首先需要将二叉树分成左右两树，然后分别针对左右两树进行高度计算，只要有子节点，高度就+1。

    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        // 左树的高度
        int leftHight =getTreeHight(root.left);
        // 右树的高度
        int rightHight =getTreeHight(root.right);
        // 判断高度差，递归
        return Math.abs(leftHight-rightHight)<=1 && isBalanced(root.left) && isBalanced(root.right);

    }
    // 获取当前节点的高度
    public int getTreeHight(TreeNode node){
        if(node == null) return 0;
        int leftHight = getTreeHight(node.left);
        int rightHight=getTreeHight(node.right);
        return Math.max(leftHight,rightHight)+1;
    }

一开始想使用层序遍历，没有考虑到是针对左右子树的情况，但是上面这种递归是采用的从上而下，计算所有的高度，时间复杂度：O(n^2)，比较浪费性能。

2.2 自底向上递归

这种方式优点类似后序遍历，左右根的方式，最左边的元素在第一个，然后如果是有并排的同属一个树的右子树，或者当前没有右子树，那么认为是平衡的，然后继续递归，直到高度不符合，退出。

  public boolean isBalanced(TreeNode root) {
        return getTreeHight(root) >=0;
    }
    // 获取当前节点的高度
    public int getTreeHight(TreeNode root){
        if(root == null) return 0;
        int leftHight = getTreeHight(root.left);
        int rightHight = getTreeHight(root.right);
        // 不满足条件leftHight=-1标识没有左子树,rightHight=-1类似
        if(leftHight == -1 || rightHight == -1 || Math.abs(leftHight-rightHight)>1){
            return -1;
        }else{
            return Math.max(leftHight,rightHight)+1;
        }
    }

3. 二叉树的最小深度

二叉树的最小深度
给定一个二叉树，找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明：叶子节点是指没有子节点的节点。

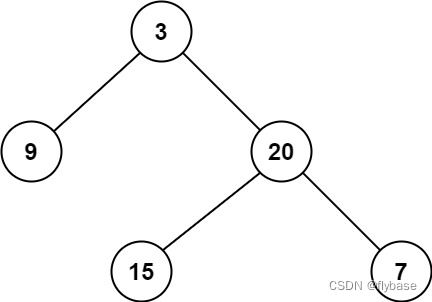
输入：root = [3,9,20,null,null,15,7]
输出：2

3.1 递归

首先左右孩子都为空，意味着是叶子节点，返回1
当左右节点有一个为空，就表示需要的深度就是另一个子树的深度+1
当左右节点都存在，就选取比较小的深度。

    public int minDepth(TreeNode root) {
      if(root == null) return 0;
      // 只有根节点,此时就是叶子节点
      if(root.left==null && root.right == null) return 1;
      // 左子树深度
      int leftLength = minDepth(root.left);
      // 右子树深度
      int rightLength = minDepth(root.right);
      // 树的深度：非空子树的深度加上根节点本身，只要有一个子树为空，那么其对应的深度就是0
      if(root.left == null || root.right == null) return leftLength+rightLength+1;
      // 左右子树都不为空，深度就是左右子树较小的加上本身
      return Math.min(leftLength,rightLength)+1;
    }

3.2 层序遍历

层序遍历就比较容易理解，只是需要判断是不是叶子节点，是叶子节点，就直接返回当前深度，不是那么就继续添加。

    public int minDepth(TreeNode root) {
     if(root ==null) return 0;
     LinkedList<TreeNode> queue = new LinkedList<>();
     queue.add(root);
     int minLength =0;
     while(!queue.isEmpty()){
       int size = queue.size();
        minLength++;
        for(int i=0;i<size;i++){
          TreeNode node =queue.remove();
          // 遇到叶子节点就返回
          if(node.left==null && node.right==null){
            return minLength;
          }

          if(node.left!=null){
            queue.add(node.left);
          }

          if(node.right!=null){
            queue.add(node.right);
          }
        }
     }
     return 0;
    }

相比于递归，层序遍历反而事件，空间比较快，因为只需要满足相应的树节点的子树都为空，就意味着找到了叶子节点，深度返回，最终一定会找到第一个叶子节点为空，那么就不需要遍历所有的二叉树了。

4. N 叉树的最大深度

N 叉树的最大深度
给定一个 N 叉树，找到其最大深度。

最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。

N 叉树输入按层序遍历序列化表示，每组子节点由空值分隔（请参见示例）。

4.1 层序遍历

这一题和二叉树类似，区别在于需要遍历子元素然后添加子元素。

 public int maxDepth(Node root) {
        if(root == null) return 0;
        LinkedList<Node> queue = new LinkedList<>();
        queue.add(root);
        int minLength = 0;
        while(!queue.isEmpty()){
            int size = queue.size();
            minLength++;
            for(int i=0;i<size;i++){
                Node node = queue.poll();
               List<Node> children = node.children;
               for(Node child:children){
                   queue.add(child);
               }
            }
        }
        return minLength;
    }

4.2 递归

    public int maxDepth(Node root) {
        if(root == null) 
            {return 0;}
        else if(root.children.isEmpty()) 
            {return 1;}
        else{
            List<Integer> hight = new ArrayList<>();
            List<Node> children = root.children;
            for(Node child:children){
                hight.add(maxDepth(child));
            }
            return Collections.max(hight)+1;
        }
    }

总结

关于二叉树的深度和高度问题，使用递归是很快速的，但是缺点在于需要考虑好边界，有的时候感觉想不到递归的解决方案，递归还是不大熟，而层序遍历容易理解和想到，但是缺点在于代码比较长。