【力扣料理手册】链表专题
基本操作
初始化
interface ListNode<T> {
data: T;
next: ListNode<T>;
}
插入
插入只需要考虑要插入位置前驱节点和后继节点(双向链表的情况下需要更新后继节点)即可,其他节点不受影响
因此在给定指针的情况下插入的操作时间复杂度为O(1)。这里给定指针中的指针指的是插入位置的前驱节点。
temp = 待插入位置的前驱节点.next
待插入位置的前驱节点.next = 待插入指针
待插入指针.next = temp
删除
只需要将需要删除的节点的前驱指针的 next 指针修正为其下下个节点即可,注意考虑边界条件。
待删除位置的前驱节点.next = 待删除位置的前驱节点.next.next
遍历
当前指针 = 头指针
while 当前节点不为空 {
print(当前节点)
当前指针 = 当前指针.next
}
dfs(cur) {
if 当前节点为空 return
print(cur.val)
return dfs(cur.next)
}
链表和数组差异
- 数组的遍历:
for(int i = 0; i < arr.size();i++) {
print(arr[i])
}
- 链表的遍历:
for (ListNode cur = head; cur != null; cur = cur.next) {
print(cur.val)
}
数组是索引 ++
链表是 cur = cur.next
- 逆序遍历
数组
for(int i = arr.size() - 1; i > - 1;i--) {
print(arr[i])
}
链表
for (ListNode cur = tail; cur != null; cur = cur.pre) {
print(cur.val)
}
- 添加元素
arr.push(1)
public class ListNode {
int val;
ListNode next;
ListNode() {}
ListNode(int val) { this.val = val; }
ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}
// 假设 tail 是链表的尾部节点
tail.next = new ListNode('lucifer')
tail = tail.next
经过上面两行代码之后, tail 仍然指向尾部节点。
数组的底层也是类似的
arr.length += 1
arr[arr.length - 1] = 'lucifer'
两个考点
指针的修改
- 头尾不断交换
数组
function reverseArray(arr) {
let left = 0;
let right = arr.length - 1;
while(left < right){
const temp = arr[left];
arr[left++] = arr[right];
arr[right--] = temp;
}
return arr;
}
链表
function reverse(head, tail, terminal){
let cur = head;
let pre = null;
while(cur != terminal){
//留下next联系方式
next = cur.next;
//修改指针
cur.next = pre;
//继续往下走
pre = cur;
cur = next;
return [tail, head];
}
}
三个注意
出现了环,造成死循环。
- 题目就有可能环,让你判断是否有环,以及环的位置。
- 快慢指针算法。
- 题目链表没环,但是被你操作指针整出环了。
分不清边界,导致边界条件出错。
- 如果题目的头节点可能被移除,那么考虑使用虚拟节点,这样头节点就变成了中间节点,就不需要为头节点做特殊判断了。
- 题目让你返回的不是原本的头节点,而是尾部节点或者其他中间节点,这个时候要注意指针的变化。
搞不懂递归怎么做
- 反转链表的前序遍历
- 尾递归
def dfs(head, pre):
if not head: return pre
# 留下联系方式(由于后面的都没处理,因此可以通过 head.next 定位到下一个)
next = head.next
# 主逻辑(改变指针)在进入后面节点的前面(由于前面的都已经处理好了,因此不会有环)
head.next = pre
dfs(next, head)
dfs(head, None)
- 后序遍历
def dfs(head):
if not head or not head.next: return head
# 不需要留联系方式了,因为我们后面已经走过了,不需走了,现在我们要回去了。
res = dfs(head.next)
# 主逻辑(改变指针)在进入后面的节点的后面,也就是递归返回的过程会执行到
head.next.next = head
# 置空,防止环的产生
head.next = None
return res
- 如果是前序遍历,那么你可以想象前面的链表都处理好了,怎么处理的不用管。
- 相应地如果是后序遍历,那么你可以想象后面的链表都处理好了,怎么处理的不用管。
四个技巧
虚拟头
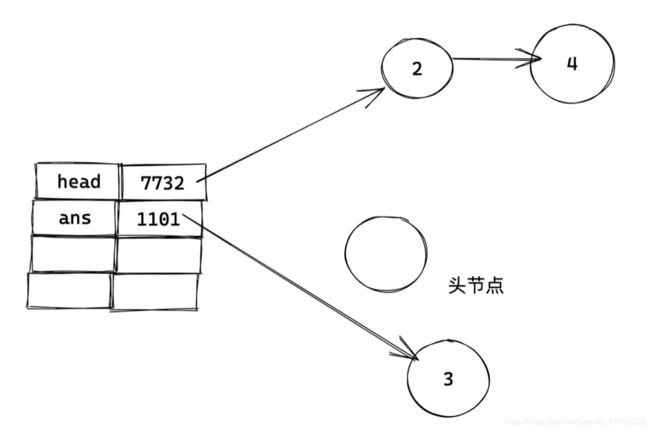
Q1:ans.next指向什么?
ans = ListNode(1)
ans.next = head
head = head.next
head = head.next
A1: 最开始的 head。
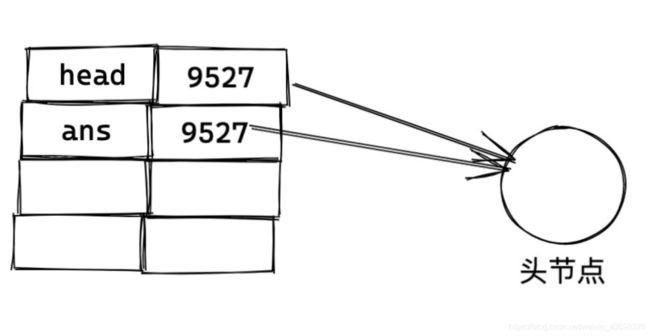
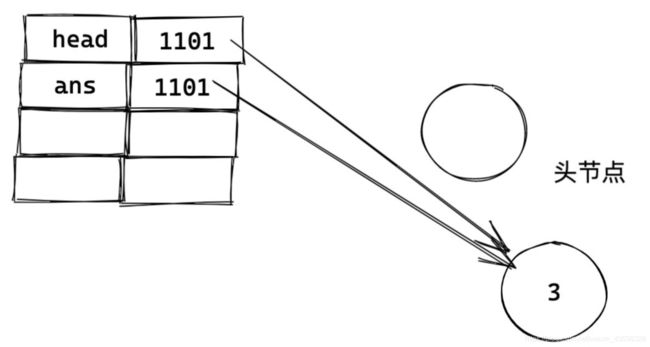
之后执行 head = head.next (ans 和 head 被切断联系了),此时的内存图:
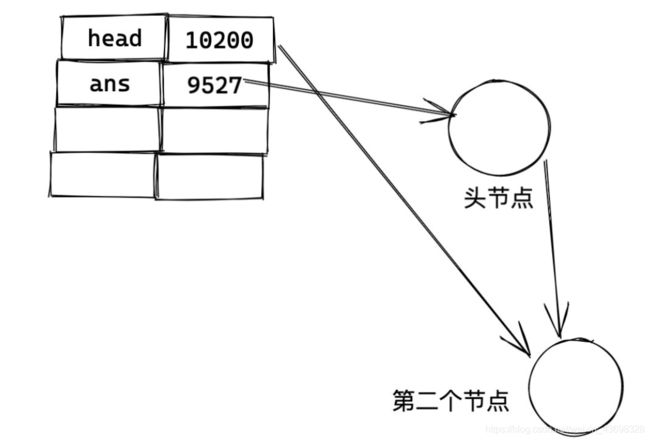
不难看出,ans 没变
Q2:ans.next指向什么?
ans = ListNode(1)
head = ans
head.next = ListNode(3)
head.next = ListNode(4)
A2: ListNode(4)
head.next = ListNode(3)
head.next = ListNode(4)
head.next = ListNode(4) 也是同理。因此最终的指向 ans.next 是 ListNode(4)。
Q3: 如下代码 ans.next 指向什么?
ans = ListNode(1)
head = ans
head.next = ListNode(3)
head = ListNode(2)
head.next = ListNode(4)
A3: ListNode(3)
ans = ListNode(1)
head = ans
head.next = ListNode(3)
按照上面的分析,此时 head 和 ans 的 next 都指向 ListNode(3)。关键是下面两行:
head = ListNode(2)
head.next = ListNode(4)
指向了 head = ListNode(2) 之后, head 和 ans 的关系就被切断了,当前以及之后所有的 head 操作都不会影响到 ans,因此 ans 还指向被切断前的节点,因此 ans.next 输出的是 ListNode(3)。
- 头节点是最常见的边界,如果我们用一个虚拟头指向头节点,虚拟头就是新的头节点了,而虚拟头不是题目给的节点,不参与运算,因此我们不需要特殊判断。
- 如果题目需要返回链表中间的某个节点,实际上也可以借助虚拟节点,新建一个虚拟头,让虚拟头在恰当的时候(刚好指向需要返回的节点)断开连接
K个一组翻转链表
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
示例:
给你这个链表:1->2->3->4->5
当 k = 2 时,应当返回: 2->1->4->3->5
当 k = 3 时,应当返回: 3->2->1->4->5
说明:
你的算法只能使用常数的额外空间。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
思路
- 以k个nodes为一组进行翻转,返回翻转后的linked list
- 从左往右扫描一遍linked list,扫描过程中,以k个单位把数组分成若干段,对每一段就行翻转。
- 给定首位nodes,如何对链表进行翻转。
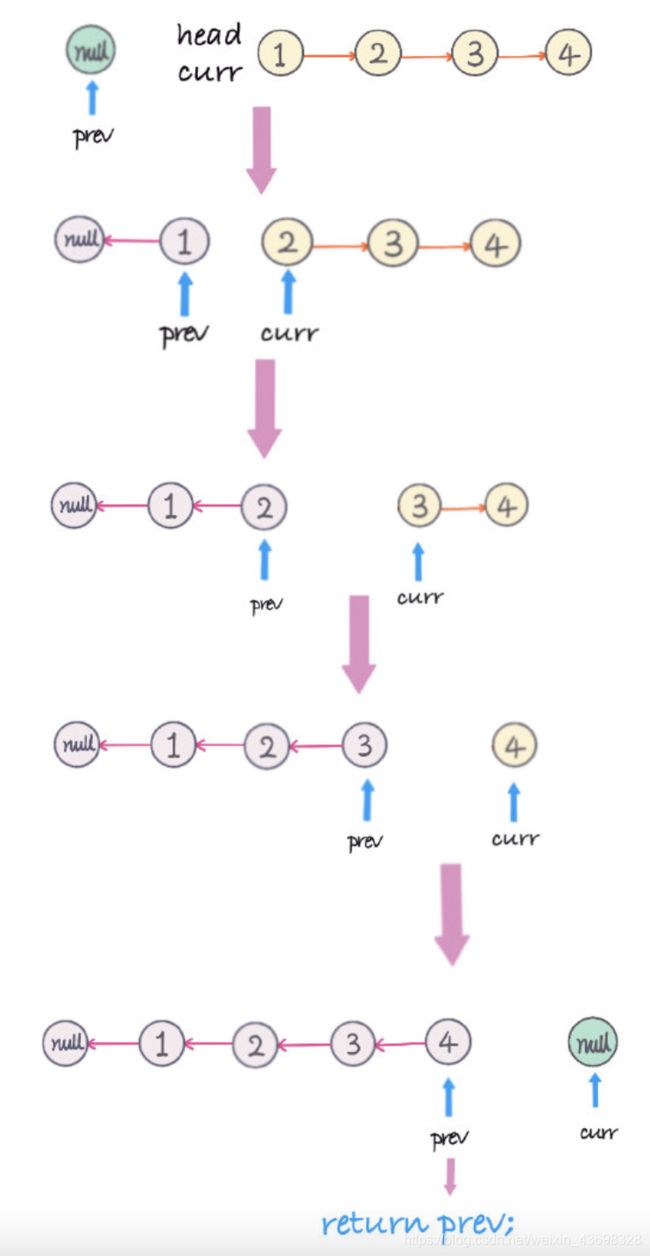
- 链表的翻转过程,初始化一个为null的
previous node,遍历链表的同时,当前node(cur)的下一个(next)指向前一个node(pre),在改变当前node的指向前,用一个临时变量记录当前node的下一个node(cur.next)
List temp = cur.next;
cur.next = pre;
pre = cur;
cur = temp;
然后是对每一组(k个nodes)进行翻转
- 先分组,用一个count记录当前节点个数
- 用start记录当前分组的起始节点位置的前一个节点
- 用end记录最后一个节点的位置
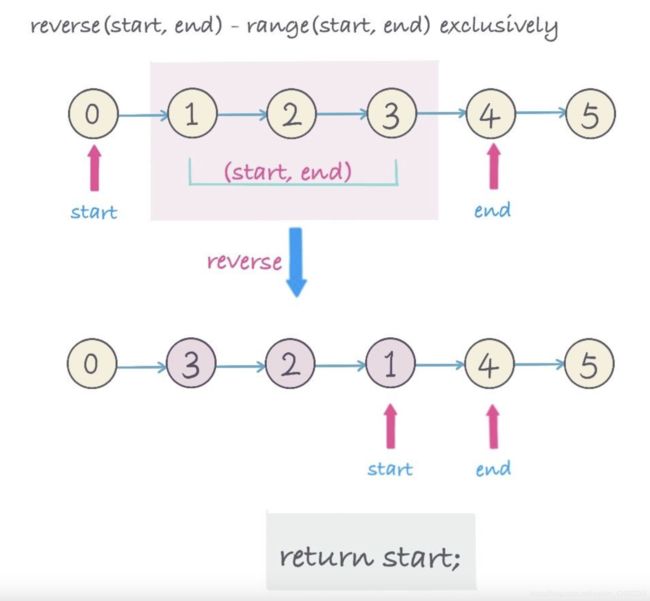
- 翻转一组,(start,end)
- 翻转后,start指向翻转后的链表,区间(start,end)中的最后一个节点,返回start节点
- 如果不需要翻转,end就往后移动一个(end = end.next),每一次移动,都要count+1
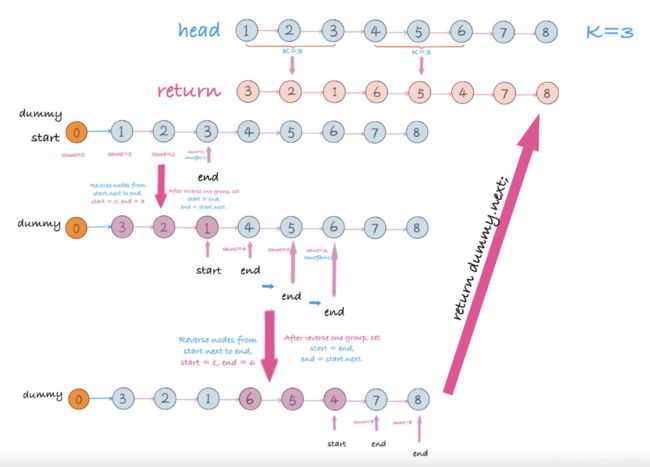
步骤4和5如图
关键点分析
- 创建一个dummy node
- 对链表以k为单位进行分组,记录每一组的起始和最后节点位置
- 对每一组进行翻转,更换起始和最后的位置
- 返回dummy.next
class ListNode{
constructor(val, next){
this.val = val;
this.next = next;
}
}
var reverseKGroup = function (head, k) {
// 标兵
let dummy = new ListNode();
dummy.next = head;
let [start, end] = [dummy, dummy.next];
let count = 0;
while (end) {
count++;
if (count % k === 0) {
start = reverseList(start, end.next);
end = start.next;
} else {
end = end.next;
}
}
return dummy.next;
//链表的翻转过程,初始化一个为null的`previous node`,
//遍历链表的同时,当前node(cur)的下一个(next)指向前一个node(pre),
//在改变当前node的指向前,用一个临时变量记录当前node的下一个node(cur.next)
// 翻转stat -> end的链表
function reverseList(start, end) {
let [pre, cur] = [start, start.next];
const first = cur;
while (cur !== end) {
let next = cur.next;
cur.next = pre;
pre = cur;
cur = next;
}
start.next = pre;
first.next = cur;
console.log(first)
return first;
}
}
console.log(reverseKGroup(new ListNode(3, new ListNode(2, new ListNode(1, new ListNode(4, new ListNode(5))))), 2))
扩展1
要求从后往前以k个为一组进行翻转
例子,12345678,k=3
从后往前以k=3为一组
678 876
345 543
12 直邮2个nodes少于k=3个,不翻转
最后返回12543876
思路:
- 翻转链表
- 对翻转后的链表进行从前往后以k为一组翻转
- 翻转步骤2得到的链表
例子:12345678,k=3
- 翻转链表得到:87654321
- 以k为一组翻转:67834521
- 翻转步骤2得到的链表:12543876
链接
快慢指针
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1
输出:tail connects to node index 1
解释:链表中有一个环,其尾部连接到第二个节点。
示例 2:
输入:head = [1,2], pos = 0
输出:tail connects to node index 0
解释:链表中有一个环,其尾部连接到第一个节点。
示例 3:
输入:head = [1], pos = -1
输出:no cycle
解释:链表中没有环。
进阶:
你是否可以不用额外空间解决此题?
假设从链表开始的位置到环的入口的距离为p,慢指针在环内走了的距离为c,假设慢指针走了n步,快指针走了2n步。
那么 p+c = n
显然,从p+c这一点开始,慢指针再走n步,必然会回到这个点。【因为经过了2n步,快指针到达了这一点,所以慢指针如果再走n步,也会到达这一点】
如果让快指针从链表头开始走n步,也会到达p+c这个位置,二者相遇的第一个地方肯定是环入口。
import { nodeModuleNameResolver } from "typescript";
class ListNode {
val: number;
next: ListNode;
constructor(val, next) {
this.val = val;
this.next = next;
}
}
function detectCycle(head: ListNode) {
//初始化
let slow: ListNode = head;
let fast: ListNode = head;
let x = null;
while (fast && fast.next) {
slow = slow.next;
fast = fast.next.next;
if (fast == slow) {
x = fast;
break;
}
}
if (!x) {
return null;
}
slow = head;
while (slow != x) {
slow = slow.next;
x = x.next;
}
return slow;
}
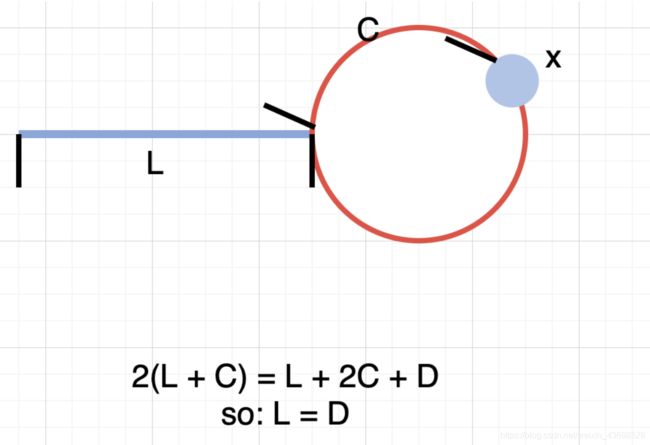
// x表示第一个集合点
// 假设L是循环的起点和起点之间的长度。
// C是入口点与x之间的长度
// D是圆的其余部分。
// 2(L + C) = L + 2C + D
// so:L = D
// 因此,我们设置了两个指针,步长范围从一到两个。当两个指针相遇时,慢点再次从起点开始,快点继续。绝对可以在入口点见面,因为L = D
穿针引线
假设链表已经反转好了,那么如何将反转好的链表拼后去呢?
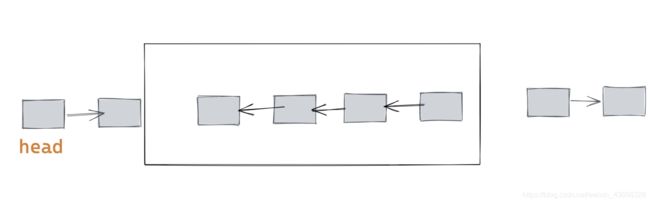
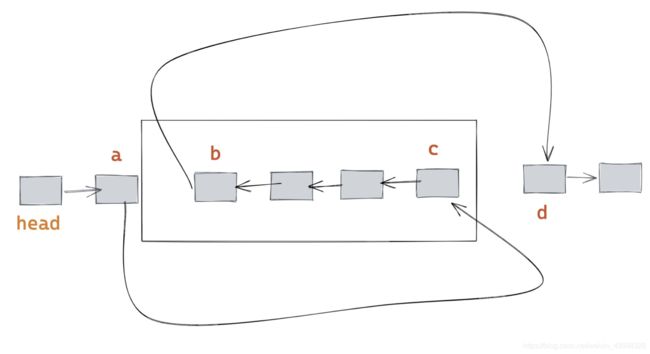
我们想要的效果是这样的:
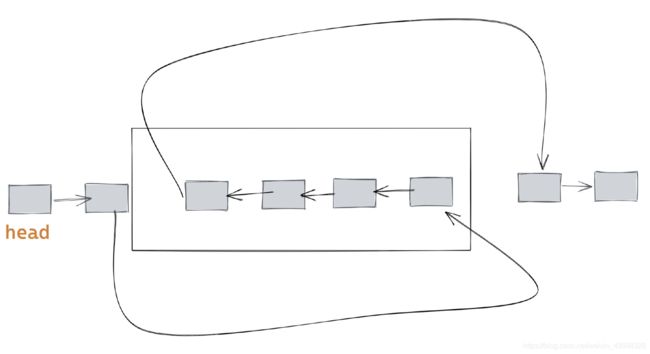
从左到右给断点编号
如图两个断点,共涉及4个node,于是编号为abcd
ab分别是需要反转的链表部分的前驱和后继(不参与反转)
b和c是需要反转的部分的头和尾
因此除了 cur, 多用两个指针 pre 和 next 即可找到 a,b,c,d。
a.next = c
b.next = d
先穿再排后判空
比如:链表反转
let [cur, pre] = [head, null];
while(cur != tail){
//留下联系方式
next = cur.next;
//修改当前指针 指向pre
cur.next = pre;
//继续向下走
pre = cur;
cur = next;
}
先穿
这里的穿是直接修改指针,包括反转链表的修改指针和穿针引线的修改指针。先别管顺序,先穿
再排
穿完之后,代码的总数已经确定了,无非就是排列组合让代码没有bug
- 因此第二部考虑顺序,那上面的两行代码哪个在前?
- 应该是先next = cur.next,原因在于后一条语句执行后cur.next就变了
- 由于上面代码的作用是反转,那么其实经过cur.next = pre之后的链表就断开了,也就是说cur后面的就访问不到了,空指针,因此此时只能返回头节点这一个节点
我们需要考虑的仅仅是被改变next指针的部分。
比如cur.next = pre的cur被改了next,因此下面用到了cur.next的地方就要考虑放哪,其他代码不用考虑
后判空
和上面的原则类似,穿完之后,代码的总数已经确定了,无非就是看看哪行代码会空指针异常。
和上面的技巧一样,我们很多时候没有必要全考虑。我们需要考虑的仅仅是被改变 next 指针的部分。
while cur:
cur = cur.next
我们考虑 cur 是否为空呢? 很明显不可能,因为 while 条件保证了,因此不需判空。
那如何是这样的代码呢?
while cur:
next = cur.next
n_next = next.next
如上代码有两个 next,第一个不用判空,上面已经讲了。而第二个是需要的,因为 next 可能是 null。如果 next 是 null ,就会引发空指针异常。因此需要修改为类似这样的代码:
while cur:
next = cur.next
if not next: break
n_next = next.next