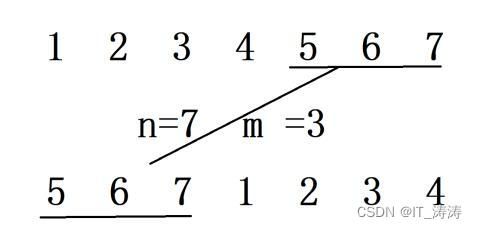有n个整数,使前面各数顺序向后移m个位置,最后m个数变成最前面m 个数

引言

这道题实现起来不是很困难，但是用最优的方法去实现，还是有一定的难度，尤其是对于初学者，很难想到最优的方法。每一种方法的时间复杂度和空间复杂度都有所差别，这篇文章主要是在该问题的基础上，分析各种方法的优劣，用空间复杂度，时间复杂度来衡量一个算法好坏。

题目再现

有n个整数,使前面各数顺序向后移m个位置,最后m个数变成最前面m 个数,见图。写一函数实现以上功能，在主函数中输入n个整数和输出调整后的n个数。

分析

思路一

图示理解

算法设计

• 将arr[len-1]保存在temp;
• 将剩余数组元素，依次从后向前遍历
  • 进行数据移动 arr[j+1] = arr[j] ;
• 将最后的数移动到最前面 arr[0]= temp

编程实现

void move1(int* arr, int len, int m) {//arr是数组，len是数组长度，m是需要移动的个数
	int temp,count = 0; //
	while (count < m) { //循环次数控制
		temp = arr[len - 1];
		//进行数据移动
		for (int j = len - 1-1; j >= 0; j--) {
			arr[j + 1] = arr[j];
		}
		arr[0] = temp;
		count++;
	}
}

算法分析

当m为1时，需要访问n个元素，m为2时，需要访问n+n个元素，m为n时，需要访问nn个元素，访问的总次数为n+2n+3n+……nn=n(n+nn)/2,平均次数为(n+nn)/2，所以时间复杂度为O(n^2),没有开辟新的空间，所以空间复杂度为O(1)

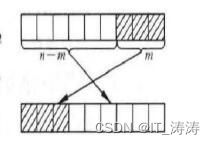
思路二

图示理解

算法设计

• i从n-m开始遍历arr，j从0开始遍历brr
  • 将arr中的元素放入brr ，循环赋值m次
• i从0开始遍历arr，j从上次遍历的位置开始遍历brr
  • 将arr中的元素放入brr ，循环赋值n-m次
• brr中的值依次赋值给arr

编程实现

//#define SIZE 7
void move2(int* arr, int len, int m) {
	int brr[SIZE] = { 0 };
	int j = 0;//j需要在第一次的赋值基础上再赋值，作用域比i大
	for (int i = len - m; i < len; i++,j++) {
		brr[j] = arr[i];
	}
	for (int i = 0; i < len - m; i++,j++) {
		brr[j] = arr[i];
	}
	for (int i = 0; i < len; i++) {
		arr[i] = brr[i];
	}
}

算法分析

变量i访问了n个元素，变量j也访问了n个元素，一共访问了2n个元素，所以时间复杂度是O(n),由于开辟了n个元素的空间，所以空间复杂度就是O(n)

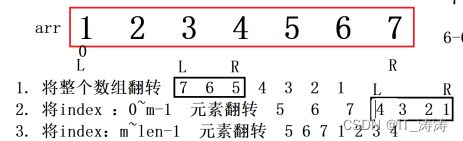
思路三

图示理解

算法设计

• 将整个数组翻转
• 将0~m-1的元素翻转
• 将m~len-1的元素翻转

翻转函数设计

• i=0开始遍历半个数组
  • 将arr[i]与arr[len-1]交换位置

编程实现

//翻转函数
void reverse(int* arr, int l_index, int r_index) {
	int num = r_index - l_index + 1; //该区间的元素个数
	int temp;
	for (int i = 0; i < num / 2; i++) { //i控制次数
		temp = arr[l_index+i];
		arr[l_index + i] = arr[r_index-i];
		arr[r_index - i] = temp;
	}
}
//交换函数
void move3(int* arr, int len, int m) {
	reverse(arr, 0, len - 1);
	reverse(arr,0,m-1);
	reverse(arr,m,len-1);
}

算法分析

翻转一次，就要访问n个元素，翻转了三次，就是3n，所以时间复杂度为O(n),没有开辟新的空间，空间复杂度为O(1)

程序测试（第三种为例）

void reverse(int* arr, int l_index, int r_index) {
	int num = r_index - l_index + 1; //该区间的元素个数
	int temp;
	for (int i = 0; i < num / 2; i++) { //i控制次数
		temp = arr[l_index+i];
		arr[l_index + i] = arr[r_index-i];
		arr[r_index - i] = temp;
	}
}
void move3(int* arr, int len, int m) {
	reverse(arr, 0, len - 1);
	reverse(arr,0,m-1);
	reverse(arr,m,len-1);
}
int main() {
	int arr[] = {1,2,3,4,5,6,7};
	int len = sizeof(arr) / sizeof(arr[0]);
	int m = 3; 
	printf("翻转之前的数组：");
	for (int i = 0; i < len; i++) {
		printf("%-5d", arr[i]);
	}
	printf("\n");
	printf("翻转之后的数组：");
	move3(arr, len, m);
	for (int i = 0; i < len; i++) {
		printf("%-5d",arr[i]);     
	}
	printf("\n");
	return 0;
}

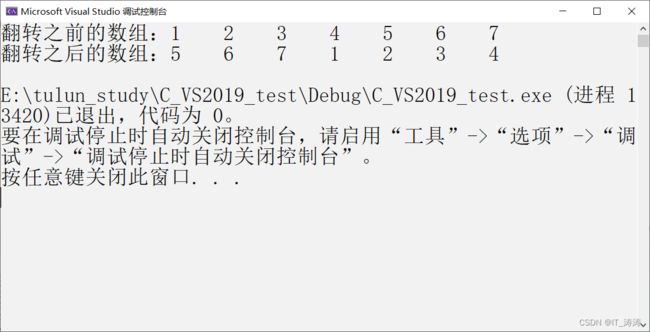
运行的结果如下