2023牛客暑期多校训练营4

 Bobo String Construction 结论，字符串哈希

Election of the King 二分查找

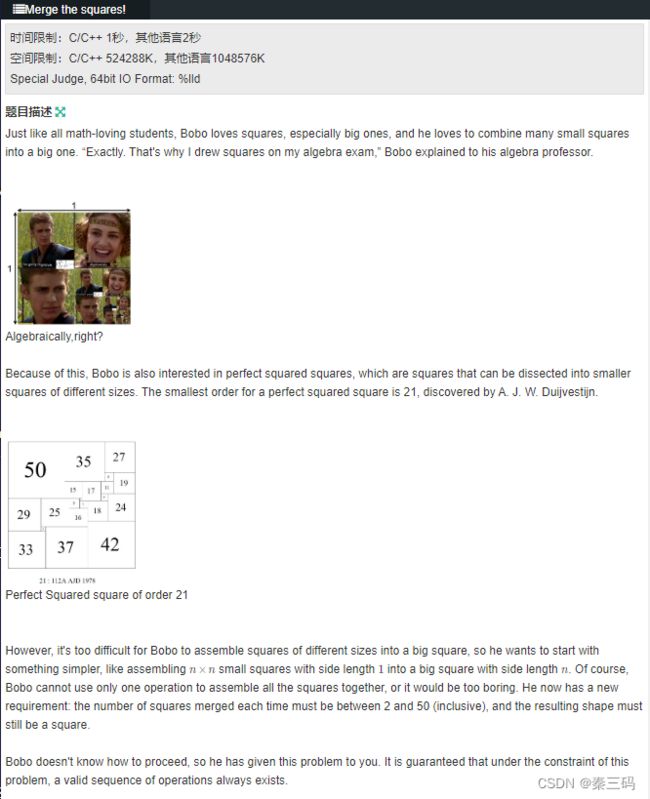
Merge the squares! 递归模拟，辗转相除法

Qu'est-ce Que C'est? DP，前缀和优化

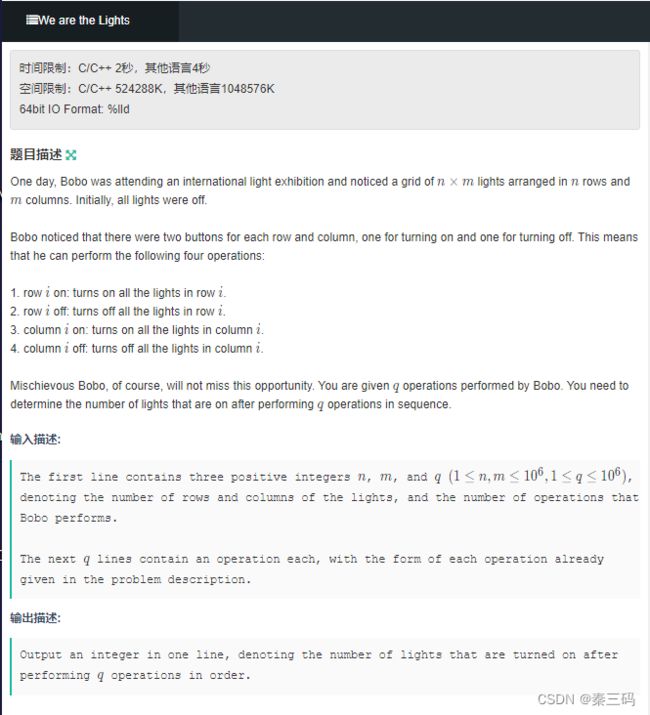
We are the Lights 思维，倒推

猜测是，把n个字符全填0或者1是最优的。所以只需要字符串哈希检查是否两个串里面含有给定串即可。 

 

#include 

using namespace std;
typedef long long int ll;
# define p1 13331
# define p2 1331
# define mod1 998244353
# define mod2 1000000007
ll base1[5000+10],base2[5000+10],sum1[5000+10],sum2[5000+10],ans1,ans2;
int n,m;
ll getsum1(int l,int r)
{
    ll ans=((sum1[r]-(sum1[l-1]*base1[r-l+1]%mod1)%mod1)%mod1+mod1)%mod1;
    return ans;
}
ll getsum2(int l,int r)
{
    ll ans=((sum2[r]-(sum2[l-1]*base2[r-l+1]%mod2)%mod2)%mod2+mod2)%mod2;
    return ans;
}
int main()
{
    int t;
    cin>>t;
    base1[0]=base2[0]=1;
    for(int i=1; i<=5000; i++)
    {
        base1[i]=p1*base1[i-1]%mod1;
        base2[i]=p2*base2[i-1]%mod2;
    }

    while(t--)
    {
        cin>>n;
        string s;
        cin>>s;
        string pres=s;
        m=s.length();
        s=" "+s;
        ans1=0,ans2=0;
        for(int i=1; i<=m; i++)
        {
            ans1=(ans1*p1%mod1+(int)(s[i]-'0'))%mod1;
            ans2=(ans2*p2%mod2+(int)(s[i]-'0'))%mod2;
        }
        string temp1=s;
        for(int i=1; i<=n; i++)
        {
            temp1+='1';
        }
        temp1+=pres;
        string temp2=s;
        for(int i=1; i<=n; i++)
        {
            temp2+='0';
        }
        temp2+=pres;

        int len1=pres.length()*2+n,len2=len1;

        for(int i=1; i<=len1; i++)
        {
            sum1[i]=(sum1[i-1]*p1%mod1+(int)(temp1[i]-'0'))%mod1;
            sum2[i]=(sum2[i-1]*p2%mod2+(int)(temp1[i]-'0'))%mod2;
        }
        int flag=0;
        for(int i=2; i+m-1

 

首先，对数组进行排序。以1 2 3 4 5为例，>=3的全部都投向5，否则都投给1。我们只需要获得当前[L,R]区间的(A[L]+A[R]) /2，如果(A[L]+A[R])恰好整除2，则全部大于等于这个值的都投给右侧，如果不能整除2，即为某.5，同样全部大于这个值的都投给右侧，故采用upper_bound,再pos--，即获得投给左侧的全部。

# include
using namespace std;
typedef long long int ll;
struct node
{
    int id,val;
    friend bool operator<(node x, node y)
    {
        return x.val>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&s[i].val);
        s[i].id=i;
    }
    sort(s+1,s+1+n,cmp);
    int l=1,r=n;
    for(int i=1;i<=n-1;i++)
    {
        int now=(s[l].val+s[r].val)/2;
        struct node temp;
        temp.id=0;
        temp.val=now;
        int mid=upper_bound(s+l,s+1+r,temp)-s;
        mid--;
        int flag=0;
        if(s[mid].val==now)
            flag++;

        if(mid-l+1>=r-mid)
        {
            r--;
        }
        else
        {
            l++;
        }
    }
    cout<

 

 首先，当n包含某个因子的时候，如果这一因子小于等于7，大于1，就可以合并每个因子*因子的正方形。但当n为质数的时候，这一方法失效。故考虑构造正方形n*n为四部分，

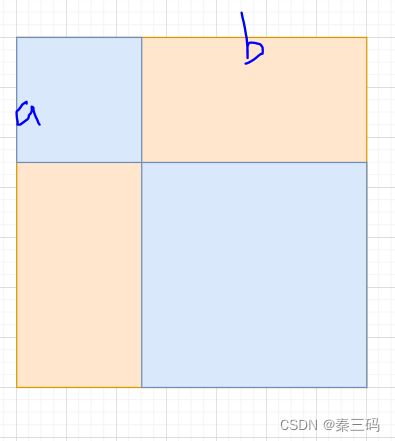
n*n=(a+b)*(a+b)。对于黄色长方形，按照辗转相处法构造，即每次以较短边为边长构造正方形。对于蓝色正方形，我们继续按照这一规则，递归构造。而当前n选择的a,b值，可以暴力枚举n的a值，检验这个a*b的长方形构造出的正方形个数是否满足2*cnt+2<=50.即我们假定蓝色已经递归构造成功。值得注意的是，因为任意正方形一定是n*n的平方数，故我们一定可以找到a,b。而对于是否有界，并不会做充分证明。

 

 

#include 
using namespace std;
typedef long long int ll;
int ans[1010],n;
bool check(int x,int y)
{
    if(y==0)
    {
        return x<=7;
    }
    int cnt=0;
    int a=x,b=y,c;
    while(b)
    {
        cnt+=a/b;
        c=a;
        a=b;
        b=c%b;
    }
    return cnt*2+2<=50;
}
struct node
{
    int x,y,len;
};
stacktemp;
void dfs(int,int,int);
void workC(int,int,int,int);
void workR(int x,int y,int row,int col) //行短
{
     if(row==1)
        return ;
    int cnt=col/row;
    for(int i=1;i<=cnt;i++)
    {
        dfs(x,y+(i-1)*row,row);
    }
    int yu=col%row;
    if(yu)
    {
        workC(x,y+(cnt)*row,row,yu);
    }
}
void workC(int x,int y,int row,int col)
{
    if(col==1)
        return ;

    int cnt=row/col;
    for(int i=1;i<=cnt;i++)
    {
        dfs(x+(i-1)*col,y,col);
    }
    int yu=row%col;
    if(yu)
    {
        workR(x+cnt*col,y,yu,col);
    }
}
void dfs(int x,int y,int len)
{
    if(len==1)
        return;
    struct node now;
    now.len=len;
    now.x=x;
    now.y=y;
    temp.push(now);
    if(ans[len]==0)
        return ;
    int a=len-ans[len],b=ans[len];
    workR(x+a,y,b,a);
    workC(x,y+a,a,b);
    dfs(x,y,a);
    dfs(x+a,y+a,b);
    return ;
}
int main()
{
   cin>>n;
   for(int i=1;i<=n;i++)
   {
       ans[i]=-1;
       for(int j=0;j<=i/2;j++)
       {
           if(check(i-j,j))
           {
               ans[i]=j;
              // break;
           }
       }
   }

   dfs(1,1,n);
   cout<

 

首先如果仅看两两之和大于等于0是很难转移的。不妨强制两种块，一种是一个正数，一种是一个负数和一个正数。这样可以获得类似于 负正正正负正正 的局面。而至于为什么不是正负组合，主要是因为，负数在前面放置，可以满足前面块和负数之和不为负数，也方便存储。缺点是，不能包含最后一个是负数的情况，故需要特判，由dp[n-1][i]*i转移。

写出暴力n^3的DP后，可以发现是可以进行前缀和优化的，且需要两个前缀和。第二个前缀和的推导，可以借助暴力程序的画图，找出枚举规律。可见，特殊的dp枚举优化，可以通过画图直观解决。

# include
using namespace std;
typedef long long int ll;
# define mod 998244353
ll dp[5010][5010];
int sum[5010][5010];
ll sumji[5010][5010];
int main()
{
    int n;
    ll m;
    cin>>n>>m;
    if(n==1)
    {
        cout<=0)
            {
                dp[2][i]=(dp[2][i]+1)%mod;
            }
        }
        sumji[2][i]=(dp[2][i]*(ll)i)%mod;
        sum[2][i]=dp[2][i];
        if(i)
        {
            sum[2][i]+=sum[2][i-1];
            sum[2][i]%=mod;
            sumji[2][i]=(sumji[2][i]+sumji[2][i-1])%mod;
        }
    }
    for(int i=3; i<=n; i++)
    {
        for(int j=0; j<=m; j++)
        {
            dp[i][j]=(dp[i][j]+sum[i-1][m])%mod;

            ll temp=((sum[i-2][m]-sum[i-2][m-j])%mod+mod)%mod;
            
            dp[i][j]=(((dp[i][j]+sumji[i-2][m-j])%mod+(ll)(m-j)*temp%mod)%mod)%mod;
            sumji[i][j]=dp[i][j]*(ll)(j)%mod;
            sum[i][j]=dp[i][j];
            if(j)
            {
                sumji[i][j]=(sumji[i][j]+sumji[i][j-1])%mod;
                sum[i][j]=(sum[i][j]+sum[i][j-1])%mod;
            }
        }
    }
    ll ans=0;
    ans+=sum[n][m];
    ans%=mod;
    ans+=sumji[n-1][m];
    ans%=mod;
    cout<

 

 倒着推，但凡倒着推先点亮的，必定点亮，反之已然。然后就可以画图解决去重问题，利用点亮行的数量，关闭行的数量，点亮和关闭列的数量即可。

# include
using namespace std;
typedef long long int ll;
int bookhang[1000000+10],booklie[1000000+10],n,m;
struct node
{
    int flag,id,on;
};
struct node s[1000000+10];
int main()
{
    cin.tie(0);
    ios::sync_with_stdio(0);
    int n,m;
    cin>>n>>m;
    int t;
    cin>>t;
    for(int i=1;i<=n;i++)
    {
        bookhang[i]=-1;
    }
    for(int i=1;i<=m;i++)
    {
        booklie[i]=-1;
    }
    for(int i=1;i<=t;i++)
    {
        string ch;
        cin>>ch;
        int id;
        string on;
        cin>>id>>on;
        if(ch[0]=='r')
        {
            s[i].flag=1;
        }
        else
        {
            s[i].flag=0;
        }
        s[i].id=id;
        if(on[1]=='n')
        {
            s[i].on=1;
        }
        else
        {
            s[i].on=0;
        }
    }

    ll ans=0;
    ll lianghang=0,guanhang=0,lianglie=0,guanlie=0;
    for(int i=t;i>=1;i--)
    {
        if(s[i].flag==1)
        {
            if(s[i].on==1)
            {
                if(bookhang[s[i].id]==-1)
                {
                    ans+=(m-lianglie-guanlie);
                    bookhang[s[i].id]=1;
                    lianghang++;
                }
            }
            else
            {
                if(bookhang[s[i].id]==-1)
                {
                    bookhang[s[i].id]=1;
                    guanhang++;
                }
            }
        }
        else
        {
            if(s[i].on==1)
            {
                if(booklie[s[i].id]==-1)
                {
                    ans+=(n-lianghang-guanhang);
                    booklie[s[i].id]=1;
                    lianglie++;
                }
            }
            else
            {
                if(booklie[s[i].id]==-1)
                {
                    booklie[s[i].id]=1;
                    guanlie++;
                }
            }
        }
    }

    cout<