LeetCode 热题 HOT 100
LeetCode 热题 HOT 100
1. 两数之和(简单-哈希表)√√
class Solution {
public:
vector twoSum(vector& nums, int target) {
unordered_map umap;
for(int i = 0; i < nums.size(); ++i){
if(umap.find(target - nums[i]) != umap.end())
return {umap[target - nums[i]], i};
umap[nums[i]] = i;
}
return {};
}
};
2. 两数相加(中等-模拟题-数学)√√
重点是当有一个链表为空了不单独处理,按节点为0处理。
class Solution {
public:
ListNode* addTwoNumbers(ListNode*l1, ListNode* l2){
ListNode* preHead = new ListNode(-1), *r = preHead;
int flag = 0;
while(l1 || l2){
int s = (l1 ? l1->val : 0) + (l2 ? l2->val : 0) + flag;
ListNode* node = new ListNode(s % 10);
r->next = node;
r = r->next;
flag = s / 10;
if(l1) l1 = l1->next;
if(l2) l2 = l2->next;
}
if(flag){
ListNode* node = new ListNode(1);
r->next = node;
}
return preHead->next;
}
};
3. 无重复字符的最长子串(中等-滑动窗口) ×!√
滑动窗口!
-
首先要判断slow需不需要更新,怎么判断?slow = max(umap[s[fast]], slow);什么意思,就是说:**umap[s[fast]]的意义是,为了在slow和fast之间不出现重复字符,slow能处于的最左位置。**如图,当j第一次到d,将umap[s[j]] = j + 1; 当再次遇到d时,slow就要判断一下,slow是不是比umap[s[j]]大,如果不是,就更新到它。
-
必须要先处理slow,也就是说,假定umap[s[fast]]已经设置好了。当fast走到重复子串的位置时,更新一下slow,怎么更新呢?就是更新到fast给slow提前安排好的位置。
-
fast到一个位置,就判断一下是否要更新slow,如何更新?用它给slow提前安排好的位置更新;
-
计算slow和fast的距离;
-
更新umap[s[fast]];
不可能先更新umap[s[fast]],再更新slow。本质上就是fast先往前走,走一步判断一下slow是否要前移。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ojGQSWt3-1675863514714)(https://pic.leetcode-cn.com/8b7cac826e572c65f8b77e0f380eaa93ab665857a8e916bc4ea36b7765eafc55-%E5%9B%BE%E7%89%87.png)]
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int res = 0;
unordered_map umap;
for(int slow(0),fast(0); fast < s.size(); ++fast){
slow = max(umap[s[fast]], slow);
res = max(res, fast - slow + 1);
umap[s[fast]] = fast + 1;
}
return res;
}
};
4. 寻找两个正序数组的中位数(困难)?
5. 最长回文子串 (中等-双指针)×√
关键点就在于回文串中点可能是一个字符,可能是两个字符。关键处见代码标注。
class Solution {
public:
int left = 0, maxLength = 0; // 只需要更新左端点和最大长度就可以
string longestPalindrome(string s) {
for(int i = 0; i < s.size(); ++i){
extend(s, i, i); // !!!!关键在这里!默认以两个字符为中点,单个字符为中点时都传i!
extend(s, i, i + 1);
}
return s.substr(left, maxLength);
}
void extend(string& s, int i, int j){
for(; i >= 0 && j < s.size() && s[i] == s[j]; --i, ++j){
if(j - i + 1 > maxLength){ // 如果出现更大的,更新左端点和长度
left = i;
maxLength = j - i + 1;
}
}
}
};
10. 正则表达式匹配(困难)?
https://leetcode.cn/problems/regular-expression-matching/solution/python3-ju-jue-rong-yu-fen-lei-chao-jian-onu9/
| r | o | s | ||
|---|---|---|---|---|
| r | ||||
| . | ||||
| * |
11. 盛最多水的容器(中等-双指针)√√
缩减搜索空间:
如果height[left] == height[right],比如 3 1 10 3:
那么最终的最大值一定跟3关系,因为不管时3 10 和 1 3 ,宽都变小了,高的最大值还是3,所以只要一边的高仍是3,面积一定会减少。
class Solution {
public:
int maxArea(vector& height) {
int n = height.size();
int res = 0;
for(int left(0), right(n - 1); left < right;){
int area = (right - left) * min(height[left], height[right]);
res = max(res, area);
if(height[left] < height[right]) ++left;
else --right;
}
return res;
}
};
15. 三数之和(中等-双指针) ××√
if(i && nums[i] == nums[i - 1]) continue; // 去重
比如 -1 -1 0 1 2不能允许第二个-1再凑一个 -1 0 1 ,但是第一个允许,可以凑-1 -1 2
if(s < 0) ++slow; // 这里不能是while,因为每次fast/slow 变化了,s 要重新计算
如果写成while(slow < fast && s < 0) ++slow; 没有任何意义,因为s没机会重新计算,slow最终只会等于fast
for(++slow; slow < fast && nums[slow] == nums[slow - 1]; ++slow);
假设 -1 -1 -1 0 1 2; -1 -1 2 是一个元组,slow前移,如果发现nums[slow] == nums[slow-1] 那必须继续前移,因为x不变,如果nums[slow]还不变,那nums[fast]肯定也不能变,就会产生重复三元组。
class Solution {
public:
vector> threeSum(vector& nums) {
sort(nums.begin(), nums.end());
vector> res;
int n(nums.size());
for(int i = 0; i < n - 2; ++i){
if(nums[i] > 0) return res;// 剪枝,如果nums[i]>0,说明后面都大于0
if(i && nums[i] == nums[i - 1]) continue; // 去重
int x = nums[i];
for(int slow(i + 1), fast(n - 1); slow < fast;){
int s = x + nums[slow] + nums[fast];
if(s < 0) ++slow; // 这里不能是while,因为每次fast/slow 变化了,s 要重新计算
if(s > 0) --fast;
if(s == 0){
res.push_back({x, nums[slow], nums[fast]});
for(++slow; slow < fast && nums[slow] == nums[slow - 1]; ++slow);
for(--fast; slow < fast && nums[fast] == nums[fast + 1]; --fast);
}
}
}
return res;
}
};
17. 电话号码的字母组合(中等-回溯)×√
这道题的关键是,不是从一个序列里面找k个字符的组合,而是从不同的字符串中寻找k个字符的排列。
class Solution {
public:
string path;
vector res;
vector tel{"", "", "abc", "def", "ghi", "jkl",
"mno", "pqrs", "tuv", "wxyz"};
vector letterCombinations(string digits) {
if(!digits.size()) return res;
DFS(digits, 0);
return res;
}
// 关键在于 startIndex是digits的下标
void DFS(string &digits, int startIndex){
// 得到数字对应的字符串在tel中的下标
int index = digits[startIndex] - '0';
// 核心在这,常规回溯
for(int i = 0; i < tel[index].size(); ++i){
path.push_back(tel[index][i]);
if(path.size() == digits.size())
res.push_back(path);
else if(startIndex + 1 < digits.size())
DFS(digits, startIndex + 1);
path.pop_back();
}
}
};
19. 删除链表的倒数第 N 个结点(中等-链表)√√
1 2 3 4 5 n = 2
- slow fast 同时指向preHead;
- fast先走两步到2;
- fast到5,slow到3;
- 注意循环结束条件是fast->next != nullptr! 才能让fast停在5。
class Solution {
public:
ListNode* removeNthFromEnd(ListNode* head, int n) {
ListNode* preHead = new ListNode(-1, head);
ListNode* slow = preHead, *fast = preHead;
for(int i(0); i < n; ++i)
fast = fast->next;
for(; fast->next; fast = fast->next){
slow = slow->next;
}
slow->next = slow->next->next;
return preHead->next;
}
};
20. 有效的括号(简单-栈) √√
class Solution {
public:
bool isValid(string s) {
unordered_map umap{{')', '('},
{']', '['},
{'}', '{'}};
stack stk;
for(auto c: s){
if(stk.empty() || umap[c] != stk.top())
stk.push(c);
else stk.pop();
}
return stk.empty();
}
};
21. 合并两个有序链表(简单-链表) √√
class Solution {
public:
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
ListNode* preHead = new ListNode(-1), *r = preHead;
while(list1 && list2){
if(list1->val < list2->val){
r->next = list1;
list1 = list1->next;
}else{
r->next = list2;
list2 = list2->next;
}
r = r->next;
}
if(list1) r->next = list1;
else r->next = list2;
return preHead->next;
}
};
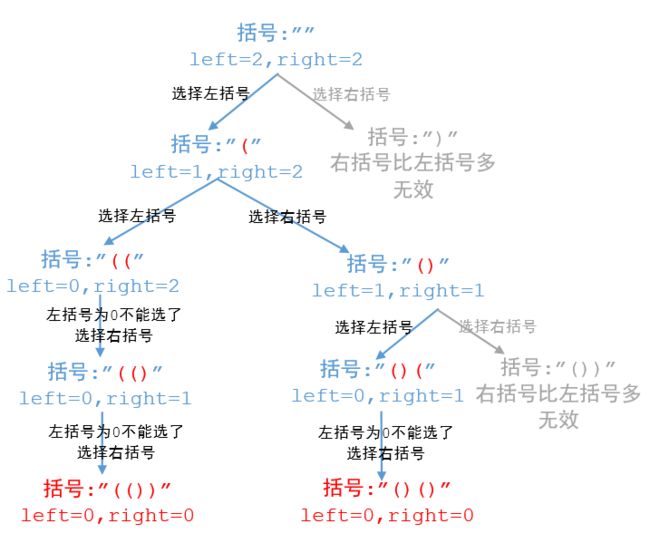
22. 括号生成(中等-DFS/回溯)×!
好像这种问有多少种组合的题,都应该往DFS/回溯上想!
动态规划也可以解,再说吧。
通过观察我们可以发现,生成的任何括号组合中都有两个规律:
- 括号组合中左括号的数量等于右括号的数量;
- 括号组合中任何位置左括号的数量都是大于等于右括号的数量。
第一条很容易理解,我们来看第二条,比如有效括号"(())()“,在任何一个位置右括号的数量都不大于左括号的数量,所以他是有效的。如果像这样”())()"第3个位置的是右括号,那么他前面只有一个左括号,而他和他前面的右括号有2个,所以无论如何都不能组合成有效的括号。
class Solution {
public:
vector res;
vector generateParenthesis(int n) {
dfs("", n, n);
return res;
}
void dfs(string path, int l, int r){
if(l == 0 && r == 0){
res.push_back(path);
return;
}
if(l > 0) dfs(path + '(', l - 1, r);
if(r > l) dfs(path + ')', l, r - 1);
}
};
23. 合并K个升序链表(困难-优先队列)×!×
注意function的写法,注意priority_queue用自定义cmp时需要传入cmp。
模拟题,用优先队列优化。
简单来说先把所有链表的表头依次进入优先队列(小顶堆),此时堆顶就是最小值,然后r->next = node; 如果堆顶节点的next不空,那么就把next节点继续入队,堆顶还是最小的。
因为每构建一个节点,都要判断当前k个链表哪个头节点的值是最小的,用优先队列可以把这个过程的时间复杂度降到O(1).
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeKLists(vector& lists) {
ListNode* preHead = new ListNode(-1), *r = preHead;
function cmp([](ListNode* lhs, ListNode* rhs){
return lhs->val > rhs->val;
});
priority_queue, function> pque(cmp);
for(auto l: lists){
if(l) pque.push(l);
}
while(!pque.empty()){
ListNode* node = pque.top();
pque.pop();
r->next = node;
r = r->next;
if(node->next) pque.push(node->next);
}
return preHead->next;
}
};
31. 下一个排列(中等)?
https://leetcode.cn/problems/next-permutation/solution/xia-yi-ge-pai-lie-suan-fa-xiang-jie-si-lu-tui-dao-/
32. 最长有效括号(困难)?
https://leetcode.cn/problems/longest-valid-parentheses/solution/shou-hua-tu-jie-zhan-de-xiang-xi-si-lu-by-hyj8/
33. 搜索旋转排序数组(中等-二分)×!
class Solution {
public:
int search(vector& nums, int target) {
int l = 0, r = nums.size() - 1, mid = 0;
while (l <= r) {
mid = l + (r - l) / 2;
if (nums[mid] == target) {
return mid;
}
// 如果nums[mid] >= nums[left] 说明left-mid是正序
if (nums[mid] >= nums[l]) {
// 如果target在left-mid内
//必须左右都要判断,否则就算target比nums[mid]小,也有可能在nums[mid]右面
if (target >= nums[l] && target < nums[mid]) {
r = mid - 1;
} else { // 如果不在
l = mid + 1;
}
} else { // 说明left-mid不是正序, 那么mid-right肯定是正序
if (target > nums[mid] && target <= nums[r]) {
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return -1;
}
};
34. 在排序数组中查找元素的第一个和最后一个位置(中等-二分)×!
class Solution {
public:
vector searchRange(vector& nums, int target) {
int n = nums.size(), l = 0, r = n - 1, mid = 0;
while(l <= r){
mid = l + (r - l) / 2;
if(nums[mid] >= target) r = mid - 1;
else l = mid + 1;
}
int left = l;
if(left == nums.size() || nums[left] != target) return {-1, -1};
r = n - 1;
while(l <= r){
mid = l + (r - l) / 2;
if(nums[mid] <= target) l = mid + 1;
else r = mid - 1;
}
int right = r;
return {left, right};
}
};
39. 组合总和(中等-回溯)√
class Solution {
public:
vector> res;
vector path;
vector> combinationSum(vector& candidates, int target) {
backTracking(candidates, target, 0);
return res;
}
void backTracking(vector& candidates, int target, int startIndex){
for(int i = startIndex; i < candidates.size(); ++i){
// 先进来
path.push_back(candidates[i]);
target -= candidates[i];
// 由于元素可以重复使用
if(target > 0) backTracking(candidates, target, i); // 有没有必要继续递归
if(target == 0) res.push_back(path); // 符合条件,加入结果集
// 不管是递归结束,还是符合条件加入结果集,都要弹出尾元素
target += candidates[i];
path.pop_back();
}
}
};
42. 接雨水(困难-单调栈)×!
class Solution {
public:
int trap(vector& height) {
int res = 0;
stack stk; // 单调递减栈 (注意存的不是高度是下标!)
for(int cur = 0; cur < height.size(); ++cur){
while(!stk.empty() && height[cur] > height[stk.top()]){ // 1
int bottomIndex = stk.top(); stk.pop(); // 2
if(stk.empty()) break; // 3
int l = stk.top(), r = cur; // 4
int h = min(height[l], height[r]) - height[bottomIndex]; // 5
res = res + (r - l - 1) * h; // 6
}
stk.push(cur);
}
return res;
}
};
/*
单调递减栈中存的是元素下标,不是下标单调递减,而是下标对应的元素单调递减。
整体思路:首先我们用的是单调递减栈,所以当 当前柱子高度比栈顶要大时,说明一定可以接水。
因为是 1 0 2 的关系
1: 如果栈不空,且当前柱子高度大于栈顶,说明出现了水沟
2: bottomIndex是水沟所在的下标, 然后出栈
3: 如果栈空了,说明没有左边的柱子,或者说当前是单调增的趋势,那么就把栈顶pop,然后break结束while,然后把当前的柱子下标入栈,维持单调递减栈的性质。
4: 由于刚才的bottomIndex已经出栈,所以现在栈顶元素是左柱子元素的下标
5: 水沟的高度就是左右柱子高度的最小值减去水沟的高度
6:这里要强调的是,由于计算了一个水沟之后,会出栈,因此,比如倒着的“土”,当中间的块出栈之后,
会变成“一”块,此时是不符合单调递减栈的,但是下一个柱子入栈时会一起计算这个“一”的面积。
*/
46. 全排列(中等-回溯) ×!×
对于比较生疏的2 1 3 ,因为每次大循环开始visited[]一定都是false。
1-> 2进入path,递归;
2-> 1进入path;递归;
3-> 1 2 都用过,3进入path。符合条件,path进入res;
回到2,visited[1]仍为true,所以循环到3,3入path;此时path.size() != nums.size(), 所以继续递归。将1进入path。
class Solution {
public:
vector> res;
vector path;
vector> permute(vector& nums) {
vector visited(nums.size());
backTracking(nums, visited);
return res;
}
void backTracking(vector& nums, vector& visited){
for(int i = 0; i < nums.size(); ++i){
if(visited[i]) continue;
path.push_back(nums[i]);
visited[i] = true;
if(path.size() == nums.size()){
res.push_back(path);
}else
backTracking(nums, visited);
path.pop_back();
visited[i] = false;
}
return;
}
};
48. 旋转图像(中等-模拟题(矩阵))×! √
副对角线没做过,下次找一道试一试。
对于n * n 的矩阵旋转题,首先要掌握四种翻转转的转移式,然后各种旋转都能转换成这四种翻转的组合:
上下翻转:matrix[i][j] = matrix[n - i - 1][j];
左右翻转:matrix[i][j] = matrix[i][n-j-1];
主对角线翻转:matrix[i][j] = matrix[j][i];
副对角线翻转:matrix[i][j] = matrix[n-j-1][n-i-1];
对于本题旋转90°,转移式为:matrix[i][j] = matrix[j][n-i-1]
根据上面四个转移式,可以观察到,只要把i变成n-i-1,再进行主对角线翻转,就实现了旋转90°的效果。
所以我们可以先对matrix[i][j]进行上下翻转 -> matrix[n-i-1][j]; 再进行主对角线旋转,就可以旋转90°啦。
所以不管题目千变万化,只要先想出转移式,再找到翻转的组合,就ok了。
class Solution{
public:
void rotate(vector>& matrix){
upDownRotate(matrix);
mainDiagRotate(matrix);
}
void upDownRotate(vector>& matrix){ // 上下翻转
int n = matrix.size();
for(int i = 0; i < n / 2; ++i){
for(int j = 0; j < n; ++j)
swap(matrix[i][j], matrix[n - i - 1][j]);
}
}
void leftRightRotate(vector>& matrix){ // 左右翻转
int n = matrix.size();
for(int j = 0; j < n / 2; ++j){
for(int i = 0; i < n; ++j)
swap(matrix[i][j], matrix[i][n - j - 1]);
}
}
void mainDiagRotate(vector>& matrix){ // 主对角线翻转
int n = matrix.size();
for(int i = 0; i < n - 1; ++i){
for(int j = i + 1; j < n; ++j)
swap(matrix[i][j], matrix[j][i]);
}
}
void subDiagRotate(vector>& matrix){ // 副对角线翻转
int n = matrix.size();
for(int i = 0; i < n - 1; ++i){
for(int j = 0; j < n-i-1; ++j)
swap(matrix[i][j], matrix[n-j-1][n-i-1]);
}
}
};
// 1 2 3
// 4 5 6
// 7 8 9
// second:
class Solution {
public:
void rotate(vector<vector<int>>& matrix) {
rotateUpDown(matrix);
rotateMainDjx(matrix);
}
void rotateUpDown(vector<vector<int>>& matrix){
int r = matrix.size();
int c = matrix[0].size();
for(int i = 0; i < r / 2; ++i){
for(int j = 0; j < c; ++j)
swap(matrix[i][j], matrix[r - 1 - i][j]);
}
}
void rotateMainDjx(vector<vector<int>>& matrix){
int r = matrix.size();
int c = matrix[0].size();
for(int i = 0; i < r - 1; ++i){
for(int j = i + 1; j < c; ++j)
swap(matrix[i][j], matrix[j][i]);
}
}
};
/*
自己分析一手:
updown:
matrix[i][j] = matrix[n - 1 - i][j]
main_djx:
matrix[i][j] = matrix[j][i]
leftright:
matrix[i][j] = matrix[i][n - 1 - j]
本题:
matrix[i][j] = matrix[j][n - 1 - i]
matrix[i][j]先上下翻转->matrix[n - 1 - i][j]
再主对角线翻转就ok了
*/
49. 字母异位词分组(中等-哈希)××
用for遍历unordered_map,返回的竟然不是迭代器是pair?
for遍历unordered_set,也是直接返回值,可能是我记错了。
for(auto it = uset.begin(); it != uset.end(); ++it){
cout<< *it <<" "<class Solution {
public:
vector> groupAnagrams(vector& strs) {
vector> res;
unordered_map> umap;
for(auto& str: strs){
string tmp = str; // !!!!!!!
sort(tmp.begin(), tmp.end());
umap[tmp].push_back(str);
}
for(auto& it: umap){
res.push_back(std::move(it.second));
}
return res;
}
};
第二遍又没做出来,我想到排序后用哈希了,但是我不知道给每个单词排序后,放进哈希,往vector里插入时怎么找到原来的单词。
关键是遍历每个原始strs的但此时,在循环内定义一个tmp来排序就好了。脑子瓦特了。
53. 最大子数组和(中等-动态规划/分治)√√
最后一遍看看分治法。
只需要注意dp[i]是截止i之前的最大子数组和,所以res是dp中的最大值。
class Solution {
public:
int maxSubArray(vector& nums) {
int n = nums.size();
vector dp(n); // (包含)下标为i前的最大子数组和
dp[0] = nums[0];
int res = dp[0];
for(int i = 1; i < n; ++i){
dp[i] = max(nums[i], nums[i] + dp[i - 1]);
res = max(res, dp[i]);
}
return res;
}
};
55. 跳跃游戏(中等-动态规划)××
class Solution {
public:
bool canJump(vector& nums) {
int n = nums.size();
if(n == 1) return true;
// dp[i]表示在i位置可以到达的最远距离
vector dp(n - 1); // 因为题意是能否到达最后一个下标,所以只需要到n-2
dp[0] = nums[0];
for(int i = 1; i < n - 1; ++i){
if(dp[i - 1] < i ) return false; // 如果前一个位置到不了当前位置,return false
dp[i] = max(dp[i-1], i + nums[i]);
if(dp[i] >= n - 1) return true;
}
return dp[n - 2] >= n - 1;
}
};
56. 合并区间(中等-区间问题)××
summary:没做出来是因为没想到怎么处理连续重复的情况,其实就是用双指针
这跟快慢指针不一样。
生疏!
class Solution {
public:
vector> merge(vector>& intervals) {
int n = intervals.size();
sort(intervals.begin(), intervals.end());
vector> res;
for(int slow(0); slow < n; ){
int left = intervals[slow][0]; // 记录重复区间的左端点
int right = intervals[slow][1]; // 记录重复区间的右端点
int fast = slow + 1; // 从slow下一个位置开始搜索
while(fast < n && intervals[fast][0] <= right){ // 如果发生重复
right = max(right, intervals[fast][1]); // 更新右端点
++fast;
}
res.push_back({left, right});
slow = fast; // 更新重复区间左端点
}
return res;
}
};
62. 不同路径(中等-动态规划) √√
class Solution {
public:
int uniquePaths(int m, int n) {
vector> dp(m, vector(n, 1));
for(int i = 1; i < m; ++i){
for(int j = 1; j < n; ++j)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
return dp[m - 1][n - 1];
}
};
64. 最小路径和(中等-动态规划)√
下次尝试用DFS/BFS做一下。
class Solution {
public:
int minPathSum(vector>& grid) {
int m = grid.size(), n = grid[0].size();
vector> dp(m, vector(n, grid[0][0]));
for(int j = 1; j < n; ++j)
dp[0][j] = grid[0][j] + dp[0][j-1];
for(int i = 1; i < m; ++i)
dp[i][0] = grid[i][0] + dp[i-1][0];
for(int i = 1; i < m; ++i){
for(int j = 1; j < n; ++j)
dp[i][j] = grid[i][j] + min(dp[i-1][j], dp[i][j-1]);
}
return dp[m-1][n-1];
}
};
70. 爬楼梯(简单-动态规划)√√
class Solution {
public:
int climbStairs(int n) {
if(n < 2) return n;
// vec[n]表示到达第n层有几种不同的方法,从0层开始,爬一阶到第一层,爬两阶到第二层
vector dp(n + 1); // 若n==2,那么楼等层数为n,因此是n+1
dp[1] = 1;
dp[2] = 2;
for(int i = 3; i < dp.size(); ++i){
dp[i] = dp[i - 1] + dp[i - 2];
}
return dp[n];
}
};
72. 编辑距离(困难-动态规划)×
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VsdAYRod-1675863514716)(https://pic.leetcode-cn.com/7bf05e42bb31e224d06701cf72a96cfa4ac0c4cd5fdc927ec0b6fa5198449b66-%E5%9B%BE%E7%89%87.png)]
| x | a | b | |
|---|---|---|---|
| x | 0 | 1 | 2 |
| a | 1 | 0 |
dp[i][j]表示word1前i个字符转换成word2前j个字符所用的最少操作数。
对于红框里的2,要么从他左面来,hro匹配r(hro已经变成r了)需要操作两次,hro再想匹配ro只能再操作一次添加一个o,也就是3次;
要么从左上方来,ho匹配r操作了2次,再操作一次添加一个o,一共操作3次;
要么从上方来,ho匹配r操作了一次,hor想匹配ro只需要把r改成o(操作1次);(!如果word1[i] = word2[j],那么显然不需要修改。)
word1[i - 1] == word2[j - 1];
对于这一行,因为在word1和word2前面都加了个空字符,所以在dp[i][j]里其实判断的是word1[i-]和word2[j-1].
dp[0][0]是空字符,dp[1][1]判断是才是word里的第一个字符。
class Solution {
public:
int minDistance(string word1, string word2) {
int m = word1.size(), n = word2.size();
vector> dp(m + 1, vector(n + 1));
for (int j = 0; j <= n; j++) {
dp[0][j] = j;
}
for (int i = 0; i <= m; i++) {
dp[i][0] = i;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = min(dp[i - 1][j - 1], min(dp[i][j-1], dp[i - 1][j])) + 1;
if (word1[i - 1] == word2[j - 1]) {
dp[i][j] = min(dp[i][j], dp[i - 1][j - 1]);
}
}
}
return dp.back().back();
}
};
75. 颜色分类(中等-循环不变量)×!×
基本思路:碰到0就往前放,碰到2就往后放,碰到1不用管,所有的1都会被挤到中间。
因为所有的2只要碰到就会往后放,所以就算在中间碰到0,swap之后换过来只可能是1;所以正常++i就好;
但是如果在中间遇到2,由于swap交换后有可能是0有可能是1,所以不能动i,下次循环再判断然后处理。
必须要用if else:如果没用if else ,假设1 0 2 换成0 1 2 的时候,0换完,++i , i=2,此时循环就应该结束了,因为nums[2]是2,但是由于是if,就把2又换到了中间,导致错误。
class Solution {
public:
void sortColors(vector& nums) {
/* 规定:
0: [0, zero]
1: (zero: two)
2: [two: n]
*/
int n = nums.size() - 1;
int zero = -1, two = n + 1;
for(int i = 0; i < two;){
if(nums[i] == 1){
++i;
continue;
}
if(nums[i] == 0){
++zero;
swap(nums[zero], nums[i]);
++i;
}else{
--two;
swap(nums[i], nums[two]);
}
}
}
};
76. 最小覆盖子串(困难-滑动窗口)×!
滑动窗口!
https://leetcode.cn/problems/minimum-window-substring/solution/leetcode-76-zui-xiao-fu-gai-zi-chuan-cja-lmqz/
/*
题解里讲的很清楚,这里再补充下:
1: umap_s记录的是窗口中字符出现的次数;umap_t记录的是t字符串中字符出现的次数
2: cnt维护的是s字符串[l, r]区间中满足t字符串的元素的个数,记录相对应字符的总数。新加入的字符s[l]必需,则cnt++
3: 当前元素加进窗口之后,该元素的个数仍然小于等于t中元素的个数,说明这个元素是必须的,所以++cnt
4: !这里很重要!窗口的l维护的是t中任意字符第一个出现在s中的位置,所以当umap_s[s[l]] > umap_t[s[l]],说明当前字符的数量多了,窗口左边可以右缩一个位置
5: 更新结果没什么好说的
6: 这里是要加个判断的,要不然整个s都没有覆盖到t,那么s和length的初值都没变过,是有问题的。
*/
class Solution {
public:
string minWindow(string s, string t) {
string res;
int start(0), length(INT_MAX);
unordered_map umap_s, umap_t; // 1
for (auto c: t) ++umap_t[c];
int cnt = 0; // 2
for (int l(0), r(0); r < s.size(); ++r) {
++umap_s[s[r]];
if (umap_s[s[r]] <= umap_t[s[r]]) ++cnt; // 3
// 维护窗口
while (umap_s[s[l]] > umap_t[s[l]]) --umap_s[s[l++]]; // 4
// 更新结果
if(cnt == t.size() && length > r - l + 1){ // 5
length = r - l + 1;
start = l;
}
}
if(cnt == t.size()) res = s.substr(start, length); // 6
return res;
}
};
/*
自己想了一种只用一个哈希表的办法:
1:umap存储t中字符出现的个数,也是s中需要出现的字符的个数。
2:--umap[s[r]] >= 0;说明这个字符t中出现过,需要用cnt记录下来,算进覆盖t的字串的长度里,如果 < 0 ,说明t中没有这个字符。
3:如果umap[s[l]] < 0,说明窗口左端的字符要么是t中没出现,要么比t中要求出现的次数多了->缩小窗口,同时增加该字符需要出现的次数
哈希表中val==0意味着正好满足所需。
*/
class Solution {
public:
string minWindow(string s, string t) {
string res;
int start(0), length(INT_MAX);
unordered_map umap; // 1
for (auto c: t) ++umap[c];
int cnt = 0;
for (int l(0), r(0); r < s.size(); ++r) {
if (--umap[s[r]] >= 0) ++cnt; // 2
while (umap[s[l]] < 0) ++umap[s[l++]]; // 3
if(cnt == t.size() && length > r - l + 1){
length = r - l + 1;
start = l;
}
}
if(cnt == t.size()) res = s.substr(start, length);
return res;
}
};
78. 子集(中等-回溯)×
https://leetcode.cn/problems/subsets/solution/c-zong-jie-liao-hui-su-wen-ti-lei-xing-dai-ni-gao-/
class Solution {
public:
vector> res;
vector path;
vector> subsets(vector& nums) {
backTracking(nums, 0);
return res;
}
void backTracking(vector& nums, int startIndex){
res.push_back(path);
for(int i = startIndex; i < nums.size(); ++i){
path.push_back(nums[i]);
backTracking(nums, i + 1);
path.pop_back();
}
}
};
79. 单词搜索(中等-DFS)×!×
注意只需要一个flag,每次到一个点先标记成true(已遍历过);当以这个点为起点的搜索都结束之后,再标记成false(搜索完了,后面的搜索可以再来)。
注意每次传入的index是下一个待搜索的字符,r和c传入的还是当前的坐标。只有当index没越界,才会去当前坐标的四周去搜索有没有word[index]。
class Solution {
public:
// 四个方向的下标偏移量
int dx[4] = {0, -1, 0, 1};
int dy[4] = {-1, 0, 1, 0};
bool res = false;
bool exist(vector>& board, string word) {
int m = board.size(), n = board[0].size();
vector> visited(m, vector(n, 0));
for(int i = 0; i < m; ++i){
for(int j = 0; j < n; ++j){
if(board[i][j] == word[0]){
dfs(board, word, visited, 1, i, j);
}
if(res) break;
}
}
return res;
}
void dfs(vector>& board, string& word, vector>& visited, int index, int r, int c) {
if(index >= word.size()){
res = true;
return;
}
visited[r][c] = true; // 标记成遍历过
for(int i = 0; i < 4; ++i){
int r_new = r + dx[i];
int c_new = c + dy[i];
if(inArea(board, r_new, c_new) && visited[r_new][c_new] == false // 剪枝
&& board[r_new][c_new] == word[index]){
dfs(board, word, visited, index + 1, r_new, c_new);
}
}
visited[r][c] = false; // 当以一个点为起点搜索完之后,要标记为false;
}
bool inArea(vector>& board, int r, int c){
return r >= 0 && r < board.size() && c >= 0 && c < board[0].size();
}
};
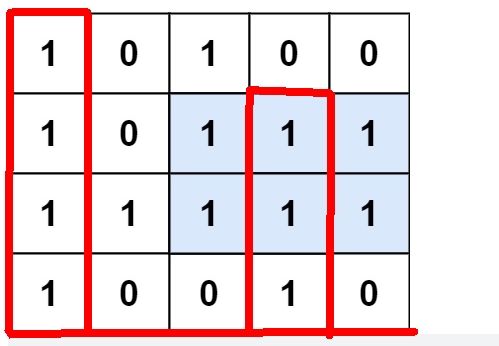
84. 柱状图中最大的矩形(困难-单调栈)×!×
对于2 1 2 来说 添加了边界变成 0 2 1 2 0 (下面为了简化说明,指的都是元素对应的元素,而不是下标)
当栈内有 0 2 时, 1 准备入栈,发现不符合单调递增栈的性质;所以对于2 来说,以2为高度的最大矩形就已经确定,就是2;
然后1入栈,2入栈;栈内有0 1 2 ;
0入栈,2为高度的矩形确定;出栈;
此时栈内还有0, 1 ;此时需要确定1为高度的矩形;
int curHeight = heights[st.top()]; st.pop(); // 1的下标出栈,这里能说明为什么必须获得了高度之后紧接着就要出栈,因为这样才能获得以1为高度的左端点的下标(因为现在栈内的0 1,原先它们之间是有个2的,只是以2为高度的矩形已经算完了,所以2出去了,但它比1大,所以可以用它作为左端点)
int left = st.top() + 1; // (因为是单调递增栈,如果0 1 是紧挨着,那么left就是1的下标(st.top() + 1)。如果原来它们之间还有元素,要么比1大,但是肯定已经出栈了,st.top() + 1 就是第一个大于1的元素的下标)
class Solution {
public:
int largestRectangleArea(vector& heights) {
heights.insert(heights.begin(), 0);
heights.push_back(0);
int res = 0;
stack stk;
for(int i = 0; i < heights.size(); ++i){
while(!stk.empty() && heights[i] < heights[stk.top()]){
int height = heights[stk.top()]; stk.pop();
int left = stk.top() + 1;
res = max(res, (i - left) * height);
}
stk.push(i);
}
return res;
}
};
85. 最大矩形(困难-单调栈)×
/*
跟84解法一样,只是要将84的解法用m - 1次求出最大值。主要还是要夯实84题。
就是以每一行为x轴算出一个柱状图的vector, 然后算出最大面积就可以了。
1:这里要注意,虽然从图里看最高的一层在顶上,但是从矩阵看它就是第一行,所以i,j都从0遍历。
2:如果当前是1,那么可以加上之前的高度,只要是0,那么就是0。
3:这里要注意不能用引用,因为解法中要对heights增加左右边界,所以要传值,不能改变heights的大小。
*/
class Solution {
public:
int maximalRectangle(vector>& matrix) {
int m = matrix.size(), n = matrix[0].size();
int res = 0;
vector heights(n);
for(int i = 0; i < m; ++i){ // 1
for(int j = 0; j < n; ++j){
if(matrix[i][j] == '1') heights[j] += matrix[i][j] - '0'; // 2
else heights[j] = 0;
}
res = max(res, largestRectangleArea(heights));
}
return res;
}
int largestRectangleArea(vector heights) { // 3
heights.insert(heights.begin(), 0);
heights.push_back(0);
int res = 0;
stack stk;
for(int i = 0; i < heights.size(); ++i){
while(!stk.empty() && heights[i] < heights[stk.top()]){
int height = heights[stk.top()]; stk.pop();
int left = stk.top() + 1;
res = max(res, (i - left) * height);
}
stk.push(i);
}
return res;
}
};
94. 二叉树的中序遍历(简单-二叉树)√√
class Solution {
public:
vector res;
vector inorderTraversal(TreeNode* root) {
inorder(root);
return res;
}
void inorder(TreeNode* root){
if(!root) return;
inorder(root->left);
res.push_back(root->val);
inorder(root->right);
}
};
96. 不同的二叉搜索树(中等)×!?
class Solution {
public:
unordered_map umap; // 1
int numTrees(int n) {
if (n <= 1) return 1;
int res = 0;
for (int i = 1; i <= n; i++) {
auto left = umap.find(i - 1);
if (left == umap.end()) {
int l = numTrees(i - 1);
umap[i - 1] = l;
}
auto right = umap.find(n - i);
if (right == umap.end()) {
int r = numTrees(n - i);
umap[i - 1] = r;
}
res += l * r;
}
return res;
}
};
98. 验证二叉搜索树(中等-二叉树)××
class Solution {
public:
TreeNode* preNode = nullptr;
bool isValidBST(TreeNode* root) {
if(!root) return true;
if(!isValidBST(root->left)) return false; // !!!!!!!!!!!!
if(preNode && (root->val <= preNode->val)) return false;
preNode = root;
return isValidBST(root->right);
}
};
101. 对称二叉树(简单-二叉树)×√
递归
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(!root) return true;
return DFS(root->left, root->right);
}
bool DFS(TreeNode* left, TreeNode* right){
if(!left && !right) return true;
if(!left || !right) return false;
if(left->val != right->val) return false;
return DFS(left->left, right->right) && DFS(left->right, right->left);
}
};
迭代
class Solution {
public:
bool isSymmetric(TreeNode* root) {
if(!root->left && !root->right) return true;
deque dque;
dque.push_back(root->left);
dque.push_back(root->right);
while(!dque.empty()){
TreeNode* first = dque.front();
dque.pop_front();
TreeNode* second = dque.front();
dque.pop_front();
if(!first && !second) continue;
if(!first || !second) return false;
if(first->val != second->val) return false;
dque.push_back(first->left);
dque.push_back(second->right);
dque.push_back(first->right);
dque.push_back(second->left);
}
return true;
}
};
102. 二叉树的层序遍历(中等-二叉树)×√
二叉树-层序遍历!
就是忘了用dque.size()去判断每次出队的数量!!!!!!
只需要定义一个vector tmp; 然后每次循环后移动出去,下次循环可以复用。有空看下移动时发生了什么。
class Solution{
public:
vector> levelOrder(TreeNode* root){
vector> res;
if(!root) return res;
deque dque;
dque.push_back(root);
vector tmp;
while(!dque.empty()){
int n = dque.size(); // !!!!!!!!!!!!!!!!!!!!
for(int i = 0; i < n; ++i){
TreeNode* node = dque.front();
dque.pop_front();
tmp.push_back(node->val);
if(node->left) dque.push_back(node->left);
if(node->right) dque.push_back(node->right);
}
res.push_back(std::move(tmp));
}
return res;
}
};
104. 二叉树的最大深度(简单-二叉树)√√
class Solution {
public:
int maxDepth(TreeNode* root) {
if(!root) return 0;
return 1 + max(maxDepth(root->left), maxDepth(root->right));
}
};
105. 从前序与中序遍历序列构造二叉树(中等-二叉树)×?
class Solution{
TreeNode* traversal(vector& inorder, vector& preorder){
if(preorder.size() == 0) return nullptr; // 递归出口
// 前序遍历数组的第一个节点就是当前的根节点
int rootValue = pretorder[0];
TreeNode* root = new TreeNode(rootValue);
if(preorder.size() == 1) return root; // 叶子节点 递归出口
//找到中序遍历数组的切割点
int delimiterIndex;
for(delimiterIndex = 0; delimiterIndex < inorder.size(); ++delimiterIndex){
if(inorder[delimiterIndex] == rootValue) break;
}
// 切割中序数组
vector leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
vector rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end());
// 舍弃前序数组的第一个元素,为了切割的左右前序数组的size与左右中序数组size一样。
preorder.erase(preorder.begin());
vector leftPreorder(preorder.begin(), preorder.begin() + leftInorder.size());
vector rightPreorder(preorder.begin() + leftInorder.size(), preorder.end());
root->left = traversal(leftInorder, leftPreorder);
root->right = traversal(rightInorder, rightPreorder);
return root;
}
public:
TreeNode* buildTree(vector& preorder, vector& inorder){
return traversal(inorder, preorder);
}
};
class Solution {
public:
TreeNode* buildTree(vector& preorder, vector& inorder) {
int pn = preorder.size(), in = inorder.size();
TreeNode* root = build(preorder, inorder, 0, pn - 1, 0, in - 1);
return root;
}
TreeNode* build(vector& preorder, vector& inorder, int ps, int pe, int is, int ie){
if(ps > pe) return nullptr;
TreeNode* root = new TreeNode(preorder[ps]);
if(pe - ps == 0) return root;
int midIndex = find(inorder.begin() + ps, inorder.begin() + pe + 1, preorder[ps]) - inorder.begin();
int preLeftStartIndex = ps + 1, preLeftEndIndex = midIndex;
int preRightStartIndex = midIndex + 1, preRightEndIndex = pe;
int inLeftStartIndex = is, inLeftEndIndex = midIndex - 1;
int inRightStartIndex = midIndex + 1, inRightEndIndex = ie;
root->left = build(preorder, inorder, preLeftStartIndex, preLeftEndIndex, inLeftStartIndex, inLeftEndIndex);
root->right = build(preorder, inorder, preRightStartIndex, preRightEndIndex, inRightStartIndex, inRightEndIndex);
return root;
}
};
114. 二叉树展开为链表(中等-二叉树)?
121. 买卖股票的最佳时机(简单-贪心)√√√
用贪心法就好,始终维护一个今天之前的最低股价,那么每天能获得最大利润就是在最低股价的那天买,在今天卖。(马后炮?是到了今天前才知道哪天的股价最低)。
最终结果就是每一天能获得的最大利润中的最大值。
class Solution {
public:
int maxProfit(vector& prices) {
int n = prices.size();
int minP = prices[0], res = 0;
for(int i = 1; i < n; ++i){
// 必须是这个顺序,因为算的是之前的利润大,还是今天的股价减去 今天之前的 最低股价 利润大
res = max(res, prices[i] - minP);
minP = min(minP, prices[i]);
}
return res;
}
};
124. 二叉树中的最大路径和(困难-二叉树) ×
https://leetcode.cn/problems/binary-tree-maximum-path-sum/solution/shou-hui-tu-jie-hen-you-ya-de-yi-dao-dfsti-by-hyj8/
我不会的点在于,从哪儿出发都可以,这怎么解决?实在没想出来。
128. 最长连续序列(中等-哈希)×!×
- 首先肯定要用到集合,一个是去重,一个是计数(哈希)。
- 统计连续元素的数量时,先判断一下e - 1 在不在集合中,在的话就continue;很好理解, 2 3 4 5 ; 当前是3的话,根本没必要统计,因为正确答案是2345。
第二遍做,忘干净了完全没思路。废物
class Solution {
public:
int longestConsecutive(vector& nums) {
unordered_set uset(nums.begin(), nums.end()); // 去重,因为后面想计数,重复就麻烦了
int res = 0;
for(auto e: uset){
int c = 1; // 记录连续元素的数量
if(!uset.count(e - 1)){
while(uset.count(++e)) ++c;
}
res = max(res, c);
}
return res;
}
};
136. 只出现一次的数字(简单-位运算) √
很简单运用了异或的性质:
- A^A = 0;
- 0和任何数字异或结果都是那个数字。
class Solution {
public:
int singleNumber(vector& nums) {
int res = 0;
for(auto e: nums){
res ^= e;
}
return res;
}
};
139. 单词拆分(中等-回溯)×
if(wordSet.find(s.substr(startIndex, i-startIndex+1)) != wordSet.end() && backtracking(s, i + 1)){
这一样的意思是,假如是这样的用例:
"aaaa"
["aaaa","aaa"]
当分离出"aaa"时,虽然在set里找到了aaa,但同时还要判断剩下的"a"行不行,行才能用当前的分割方式。
不行就i++,选中"aaaa"。
但遇到复杂的用例会超时,所以要用记忆化递归。
如下图:在1 - 3 时已经判断过以3为某个单词开头能否遍历完,但 2 - 3又要重复遍历,导致大量重复计算。
/*
1:方便查找
2:记忆数组,dp[i]表示以i下标对应的字母作为某个单词的开头,直到字符串结束能否被正确拼接出来。0表示无法拼接出来,1表示能拼接出来,-1表示还未遍历。
3:startIndex表示起始位置,当 == s.size()时,说明0 ~ s.size() - 1都被正确拼接了。
4:如果被遍历过了,直接返回结果
5:以startIndex开始直到末尾都无法被拼接
*/
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> uset(wordDict.begin(),wordDict.end()); // 1
vector<int> dp(s.size(), -1); // 2
return backTracking(s, uset, dp, 0);
}
bool backTracking(string& s, unordered_set<string>& uset, vector<int>& dp, int startIndex){
if(startIndex >= s.size()) return true; // 3
if(dp[startIndex] != -1) return dp[startIndex]; // 4
for(int i = startIndex; i < s.size(); ++i){
if(uset.find(s.substr(startIndex, i - startIndex + 1)) != uset.end() && backTracking(s, uset, dp, i + 1)){
dp[startIndex] = 1;
return true;
}
}
dp[startIndex] = 0; // 5
return false;
}
};
141. 环形链表(简单-链表)√√
class Solution {
public:
bool hasCycle(ListNode *head) {
ListNode* slow = head, *fast = head;
while(fast && fast->next != nullptr){
slow = slow->next;
fast = fast->next->next;
if(slow == fast) return true;
}
return false;
}
};
142. 环形链表 II(中等-链表)?
我完全没读懂题意。
现在我懂了,环形链表Ⅰ让判断是否有没有换,fast和slow是会相遇,但是不一定在环的入口相遇,这题让找环的入口节点。
https://leetcode.cn/problems/linked-list-cycle-ii/solution/linked-list-cycle-ii-kuai-man-zhi-zhen-shuang-zhi-/
146. LRU 缓存(中等-模拟题(算法))××
为什么要用双向链表?
- 根据题目要求,每次put都往链表头插(满足时间复杂度O(1)的要求),这样链表尾节点就是最近最久未使用的;
- 最近使用过某节点(也就是get())后,就把该节点移动到链表头;这样链表尾节点就是最近最久未使用的;
- put()正常往链表头插时间复杂度就是O(1),当超过capacity时,直接删掉最后一个节点再插入,复杂度也是O(1)。
- 因为删除尾节点时,必须要找到倒数第二个节点并修改它的next指针,所以必须是双向的。(用单链表并且定义一个指针一直指向倒数第二个节点也不行,因为删了最后一个节点还是需要再去找上一个节点,所以必须要用双向链表)。
为什么要使用unordered_map?
-
因为根据题意,get()的时间复杂度要为O(1),所以很自然的想到用哈希表。
-
当用get()访问一个节点时,需要把这个节点移动到链表头,因此val为DLinkedNode*;
其他细节
- 链表节点既要存储val,也要存储key。因为当删除尾节点时,unordered_map也要删除对应的key-value,所以要通过存储在链表节点中的key来删除。
- 尾节点也是个节点,不能简单定义成指针,要不然当链表为空的时候添加新节点还要特殊处理去修改尾指针的指向,得不偿失。
struct DLinkedNode{
int key_, val_;
DLinkedNode* prev_;
DLinkedNode* next_;
DLinkedNode(int key = 0, int val = 0): key_(key), val_(val), prev_(nullptr), next_(nullptr){}
};
class LRUCache {
public:
LRUCache(int cap): capacity_(cap), size_(0){
head_ = new DLinkedNode(); // 伪头节点
tail_ = new DLinkedNode();
head_->next_ = tail_;
tail_->prev_ = head_;
}
int get(int key) {
if(umap_.find(key) == umap_.end()) return -1; // 如果缓存里没有,返回-1
else{
DLinkedNode* node = umap_[key];
moveToHead(node); // 如果缓存里有,那么把这个节点移动到头部
return node->val_; // 返回val
}
}
void put(int key, int value) {
if(umap_.find(key) == umap_.end()){ // 如果缓存中没有
DLinkedNode* node = new DLinkedNode(key, value); // 新建节点
umap_[key] = node;
addToHead(node);
if(++size_ > capacity_){ // 如果超出了缓存容量
DLinkedNode* removed = rmTail(); // 获取删除的节点
umap_.erase(removed->key_); // 从缓存中删除
delete removed;
--size_;
}
}else{
DLinkedNode* node = umap_[key];
node->val_ = value;
moveToHead(node);
}
}
void rmNode(DLinkedNode* node){
node->prev_->next_ = node->next_;
node->next_->prev_ = node->prev_;
}
// 在原来位置删除并移动到表头
void moveToHead(DLinkedNode* node){
rmNode(node); // 将节点从原来位置删除
addToHead(node); // 添加到表头
}
// 将新节点添加到表头
void addToHead(DLinkedNode* node){
node->next_ = head_->next_; // 先修改node->next相关
node->next_->prev_ = node;
head_->next_ = node; // 再修改node->prev相关
node->prev_ = head_;
}
DLinkedNode* rmTail(){
DLinkedNode* removed = tail_->prev_;
rmNode(removed);
return removed;
}
private:
unordered_map umap_;
int size_;
int capacity_;
DLinkedNode* head_;
DLinkedNode* tail_;
};
148. 排序链表(中等-排序)×!!!
排序:归并、快排!
152. 乘积最大子数组(中等-动态规划)√√
动态规划
因为存在正负号,所以要维护两个dp状态。
class Solution {
public:
int maxProduct(vector& nums) {
// dp[i] 不能单纯由dp[i-1]推出,因为有正负号,所以要有最大最小两个状态
// dpMax[i] 表示包括nums[i]在内的最大乘积
vector dpMax(nums.size());
vector dpMin(nums.size());
dpMax[0] = nums[0];
dpMin[0] = nums[0];
int res = dpMax[0];
for(int i = 1; i < nums.size(); ++i){
// 有可能和之前乘积大,也有可能自己大
dpMax[i] = max(max(nums[i] * dpMax[i-1], nums[i] * dpMin[i-1]), nums[i]);
dpMin[i] = min(min(nums[i] * dpMax[i-1], nums[i] * dpMin[i-1]), nums[i]);
res = max(res, dpMax[i]);
}
return res;
}
};
155. 最小栈(中等-设计题(栈))×
k神写的好
主要是维护一个单调不减栈。
比如 2 1 3 1
minStk:2 1 3(跳过) 1 .
当stack出栈时,先判断一下主栈的栈顶元素是不是等于minStk的栈顶元素,是的话同时出栈。
class MinStack {
public:
stack stk;
stack minStk;
MinStack() {}
void push(int val) {
stk.push(val);
if(minStk.empty() || val <= minStk.top())
minStk.push(val);
}
void pop() {
int top = stk.top();
stk.pop();
if(top == minStk.top()) minStk.pop();
}
int top() {
return stk.top();
}
int getMin() {
return minStk.top();
}
};
160. 相交链表(简单-链表)××√
注意循环条件:while(ra != rb), 因为有交点那么就会提前相遇,没有交点也会同时为空节点,所以返回ra就是正确答案。
不能写成:
ra = ra->next ? ra->next : headB;
rb = rb->next ? rb->next : headA;
因为ra rb 永远不会都等于nullptr,无限循环
class Solution {
public:
ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
ListNode* ra = headA, *rb = headB;
while(ra != rb){
ra = ra ? ra->next : headB;
rb = rb ? rb->next : headA;
}
return ra;
}
};
169. 多数元素(简单-投票法)×√
同归于尽法,也叫投票法?
假设有100个士兵(nums),他们分属不同的阵营(阵营编号为nums[i]),他们依次冲向一个阵地并想占领阵地。
- 首先第一个冲上阵地的是nums[0]阵营的士兵,阵地上士兵数量count为1;
- 如果第i个士兵冲上阵地发现没有士兵,那么他所属的阵营就占领了阵地,count = 1;
- 如果阵地已经被占领,如果后面冲上来的士兵还是属于阵营nums[0]的;那么++count(占领士兵+1);
- 如果第i个士兵冲上阵地发现有其他阵营的士兵,那么他会冲上去与其中一个士兵同归于尽(–count;阵地上的士兵数量-1)。
```c++
class Solution {
public:
int majorityElement(vector& nums) {
int res = nums[0]; // 1
int cnt = 1;
for(int i = 1; i < nums.size(); ++i){
if(cnt == 0){ // 2
res = nums[i];
++cnt;
}else{
if(nums[i] == res) ++cnt; // 3
else --cnt;
}
}
return res;
}
};
198.打家劫舍(中等-动态规划)√√
class Solution {
public:
int rob(vector& nums) {
if(nums.size() == 1) return nums[0];
vector dp(nums.size());
dp[0] = nums[0];
dp[1] = max(nums[0], nums[1]);
for(int i = 2; i < nums.size(); ++i){
dp[i] = max(dp[i-2] + nums[i], dp[i-1]);
}
return dp[nums.size() - 1];
}
};
200. 岛屿数量(中等-DFS) √×
就是之前做对了现在又错了我有啥招。逻辑搞清啊,什么时候能进递归,逻辑要清晰。
class Solution {
public:
int dx[4] = {-1, 1, 0, 0};
int dy[4] = {0, 0, -1, 1};
int numIslands(vector>& grid) {
int m(grid.size()), n(grid[0].size()), res(0);
vector> visited(m, vector(n, false));
for(int i(0); i < m; ++i){
for(int j(0); j < n; ++j){
// 没遍历过,且是'1'才能进递归
if(!visited[i][j] && grid[i][j] == '1'){
DFS(grid, visited, i, j);
++res;
}
}
}
return res;
}
void DFS(vector>& grid, vector> &visited, int r, int c){
visited[r][c] = true;
for(int i = 0; i < 4; ++i){
int new_r = r + dx[i];
int new_c = c + dy[i];
if(inArea(grid, new_r, new_c) && !visited[new_r][new_c] && grid[new_r][new_c]== '1')
DFS(grid, visited, new_r, new_c);
}
}
bool inArea(vector>& grid, int r, int c){
return r >= 0 && r < grid.size() &&
c >= 0 && c < grid[0].size();
}
};
206. 反转链表(简单-链表)√√
class Solution {
public:
ListNode* reverseList(ListNode* head) {
ListNode* pre = nullptr;
while(head){
ListNode* next = head->next;
head->next = pre;
pre = head;
head = next;
}
return pre;
}
};
207. 课程表(中等)×!
拓扑排序 + DFS!
- 注意邻接表的结构,下标是前置课程,数组是学了前置课程才能学的后置课程。
- flags是用于记录是否是有环的。
- DFS的逻辑:深度优先,先遍历1,再去遍历1的后置课程,如果发现后置课程中的后置课程有1,那就说明存在环。
- 为什么flag可以复用,因为只要经过一次DFS,如果一个i课程无环,那么flag最后就会被设为-1,只要有环,那会直接返回false,1就没机会被改回-1了。
class Solution {
public:
bool canFinish(int numCourses, vector>& prerequisites) {
vector> adjacent(numCourses); // 邻接表
for(int i = 0; i < prerequisites.size(); ++i)
adjacent[prerequisites[i][1]].push_back(prerequisites[i][0]);
// 1表示访问过, -1表示无环
vector flags(numCourses); // 用于判断节点是否被访问, 默认是0
for(int i = 0; i < numCourses; ++i){
if(!DFS(i, adjacent, flags)) return false;
}
return true;
}
bool DFS(int i, vector> &adjacent, vector &flags){
// 递归出口
if(flags[i] == 1) return false; // 遍历过,有环
if(flags[i] == -1) return true; // 无环
flags[i] = 1; // 遍历,标记为1
for(auto j: adjacent[i]){
if(!DFS(j, adjacent, flags)) return false; // 如果存在环,return false
}
flags[i] = -1; // 没有出现环,标记为-1
return true;
}
};
208. 实现 Trie (前缀树)(中等)×
https://leetcode.cn/problems/implement-trie-prefix-tree/solution/trie-tree-de-shi-xian-gua-he-chu-xue-zhe-by-huwt/
class Trie {
public:
// 不是节点存储值,而是"边"代表值
// 没有边通向根节点,也不是一个单词的结束
bool isEnd = false;
//当某一个next不为空,说明某个字母存在
vector next;
Trie():next(26, nullptr) {}
void insert(string word) {
Trie *node = this;
for(auto c: word){
if(node->next[c - 'a'] == nullptr)
node->next[c - 'a'] = new Trie();
// 这里要注意!!不能写成node = next[c - 'a'];
// 因为这样一直用的是根节点的next!
node = node->next[c - 'a'];
}
node->isEnd = true;
}
bool search(string word) {
Trie *node = this;
for(auto c: word){
if(!node->next[c - 'a']) return false;
node = node->next[c - 'a'];
}
return node->isEnd;
}
bool startsWith(string prefix) {
Trie *node = this;
for(auto c: prefix){
if(!node->next[c - 'a']) return false;
node = node->next[c - 'a'];
}
return true;
}
// 拓展一手,实现一个代码补全:感觉就是一个简单回溯
void complete(string prefix){
trie *node = this;
for(auto c: prefix){
if(node->next[c - 'a'] == nullptr) return;
node = node->next[c - 'a'];
}
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/
215. 数组中的第K个最大元素(中等)×
221. 最大正方形(中等)×
用单调栈做出来了,效率极低。
class Solution {
public:
int maximalSquare(vector>& matrix) {
int m = matrix.size(), n = matrix[0].size();
int res = 0;
vector heights(matrix[0].size());
for(int i = 0; i < m; ++i){ // 1
for(int j = 0; j < n; ++j){
if(matrix[i][j] == '1') heights[j] += matrix[i][j] - '0';
else heights[j] = 0;
}
res = max(res, findSquare(heights));
}
return res;
}
int findSquare(vector nums){
int res = 0;
nums.emplace(nums.begin(), 0);
nums.emplace_back(0);
stack idx_stk;
for(int i = 0; i < nums.size(); ++i){
while(!idx_stk.empty() && nums[i] < nums[idx_stk.top()]){
int height = nums[idx_stk.top()];
idx_stk.pop();
int left = idx_stk.top() + 1;
int edge = min(i - left, height);
res = max(res, edge * edge);
}
idx_stk.push(i);
}
return res;
}
};
239. 滑动窗口最大值(困难-滑动窗口/单调队列)××
用一个单调递减队列(应该是单调不增),也就是que[i] 大于 que[i + 1] 4 3 3 2。
对于myQueue,它的头节点始终是当前窗口内的最大值,可能是第1个、2个、3个。
关键在于pop(),当4 3 2 在队列中, 1来了,要执行pop()确保front()是当前窗口内的最大值。
所以假设是3 4 2 1 ;一开始队列中是4 2 , 1来了要把队头出队,但是切记不能直接出队,因为3根本不在队里,只有当dque.front() == x,才需要出队。
滑动窗口流程:
- 1 首先让窗口大小不要超过限制;
- 2 根据新元素判断/更新结果;
- 3 将新元素加入窗口(根据题意,各种);
2 3 步顺序不是固定的,要具体情况具体分析:对于本题,它的窗口大小是固定的,因此必须把新元素加进窗口满足窗口大小要求,再更新结果。
class Solution {
private:
template
class myQueue{
public:
deque dque;
T front(){
return dque.front();
}
void pop(T x){
if(!dque.empty() && dque.front() == x)
dque.pop_front();
}
void push(T x){
while(!dque.empty() && x > dque.back()) dque.pop_back();
dque.push_back(x);
}
};
public:
vector maxSlidingWindow(vector& nums, int k) {
vector res;
myQueue que;
for(int i(0); i < k; ++i)
que.push(nums[i]);
res.push_back(que.front());
for(int i = k; i < nums.size(); ++i){
// 适应窗口
que.pop(nums[i - k]);
que.push(nums[i]);
res.push_back(que.front());
}
return res;
}
};
739. 每日温度(中等-单调栈)√
说来搞笑,这个题一开始我是只能想到暴力解的,然后我去看题解,先看到一个栈字,我在想跟栈有什么关系?又看到单调栈,然后一瞬间就会做了。
主要是脑子里没建立起一个哈希映射,到底什么样的题能用到单调栈?
现在我还想不到答案,按我自己做过几道单调栈的题目的经验来说,一般题目是一维数组,需要用O(n2)的暴力解来做,都可以试试单调栈(不一定能用上,但是要往这想想)。
思路:
用个单调递减栈,假设temperatures为[3,2,1,4];
- 3,2,1符合单调递减,肯定依次入栈,当i为3时,发现4大于栈顶,那么对于1来说,它的下一个最高温度就是第i = 3天,1出栈;
- 此时栈顶为1,4仍然大于2;因为是单调递减的,2和4之间要么原来没有元素,要么有元素也肯定比2小。所以2的下一个最大温度就是3 - 1 = 2天后。
- 最后栈内剩下的元素都是递减的,并且没有比他们高的温度的日期,又因为res的所有元素默认初始化为0,所以不用处理,直接返回。
- 需要强调的是栈内存储的是元素的下标!不是元素!切记!
class Solution {
public:
vector dailyTemperatures(vector& temperatures) {
int n = temperatures.size();
stack stk;
vector res(n);
for(int i = 0; i < n; ++i){
while(!stk.empty() && temperatures[i] > temperatures[stk.top()]){
int d = stk.top(); stk.pop();
res[d] = i - d;
}
stk.push(i);
}
return res;
}
};