LeetCode热题100(hot100) 一
简单(一)
- 1、[两数之和(1)](https://leetcode.cn/problems/two-sum/)
-
- 方法一 哈希字典
- 方法二 暴力法
- 2、[有效括号(20)](https://leetcode.cn/problems/valid-parentheses/submissions/)
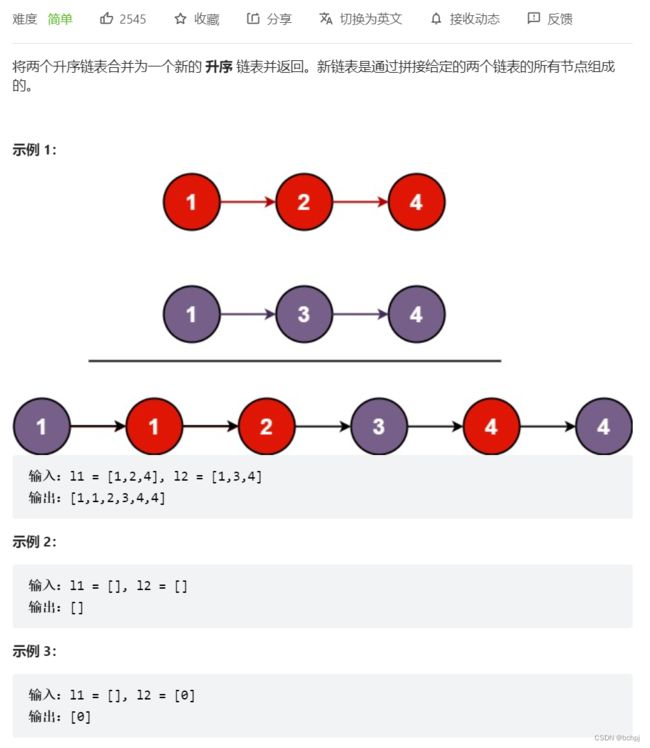
- 3、[合并两个有序链表(21)](https://leetcode.cn/problems/merge-two-sorted-lists/)
-
- 方法一 递归
- 方法二 迭代
- 4、[最大子数组和(53)](https://leetcode.cn/problems/maximum-subarray/)
- 5、[爬楼梯(70)](https://leetcode.cn/problems/climbing-stairs/)
1、两数之和(1)
方法一 哈希字典
给出x和目标值target求y=x-target,利用字典求解
1、循环数组nums中的数,利用字典存储nums中的数及对应下标
2、给出判断条件,当target-x在字典中时,返回下标
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
table = dict()
for i, num in enumerate(nums):
if target-num in table:
return [table[num], i]
table[num] = i
return []
方法二 暴力法
双重循环嵌套,先固定左边的数,依次判断后面是否有匹配的值
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
for left in range(len(nums)):
for right in range(left+1, len(nums)):
if nums[left] + nums[right]==target:
return [left, right]
return []
2、有效括号(20)
1、先判断极端情况,即len(s)不是2的整数倍
2、利用字典存储括号,右括号为key,左括号为valu
3、观察题目可以发现,括号都是先进后出,使用栈
4、循环s中的值,确定判断条件(当key=a在字典中时,判断栈stack中的最后一个元素是否时a对应的value)
5、如果满足4中的条件,弹出最后的一个元素。
6、如果a不是字典的key,将a存入栈
7、最终如果栈中为空,则返回True,否则返回False
class Solution:
def isValid(self, s: str) -> bool:
if len(s)%2 != 0:
return False
dicts = {")": "(", "]":"[", "}":"{"}
stack = list()
for a in s:
if a in dicts:
if not stack or stack[-1]!=dicts[a]:
return False
stack.pop()
else:
stack.append(a)
return not stack
当利用字典存储括号,左括号为key,右括号为value时
class Solution:
def isValid(self, s: str) -> bool:
if len(s) % 2 != 0:
return False
dicts = {"(": ")", "[":"]", "{":"}"}
stack = list()
for a in s:
if a in dicts:
stack.append(a)
else:
if not stack or dicts[stack[-1]]!=a:
return False
else:stack.pop()
return not stack
3、合并两个有序链表(21)
方法一 递归
1、判断链表l1,l2为空的情况
2、按照升序递归的指向下一个节点
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
if list1 is None:
return list2
if list2 is None:
return list1
elif list1.val < list2.val:
list1.next = self.mergeTwoLists(list1.next, list2)
return list1
else:
list2.next = self.mergeTwoLists(list2.next, list1)
return list2
方法二 迭代
1、创造一个头结点pre
2、当l1当前节点的值大于l2时,pre指向l2
3、当l1当前节点的值小于l2时,pre指向l1
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeTwoLists(self, list1: Optional[ListNode], list2: Optional[ListNode]) -> Optional[ListNode]:
prehead = ListNode(-1)
pre = prehead
while list1 and list2:
if list1.val<=list2.val:
pre.next = list1
list1 = list1.next
else:
pre.next = list2
list2 = list2.next
pre = pre.next
pre.next = list1 if list1 is not None else list2
return prehead.next
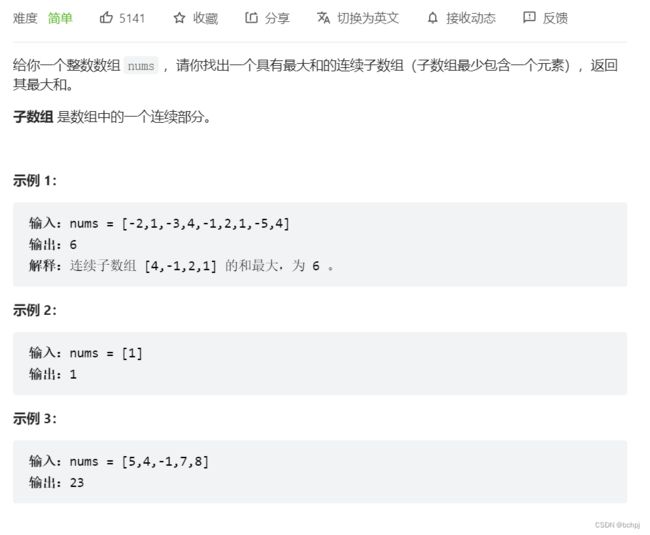
4、最大子数组和(53)
利用动态规划处理
1、分析题目可以看到,以i元素结尾的连续子数组的和为dp[i-1]+nums[i],可以得到动态规划方程dp[i] = max(dp[i-1]+nums[i], nums[i]),求得到以i元素结尾的连续子数组的最大值
2、确定初始值,dp[0]=nums[0],还需要比较所有的dp谁更大因此设定res=nums[0]
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n = len(nums)
if n== 0:
return 0
dp = [0 for _ in range(n)]
dp[0] = nums[0]
for i in range(1, n):
if dp[i - 1] >= 0:
dp[i] = dp[i - 1] + nums[i]
else:
dp[i] = nums[i]
return max(dp)
# 利用滚动变量进行优化后的代码
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
n= len(nums)
dp = 0
res = nums[0]
for i in range(n):
dp= max(nums[i], dp+ nums[i]) # 找出以nums[i+1]元素结尾的连续子序列和的最大值
res = max(res, dp) # 找出所有的子序列中和最大的那个
return res
参考资料
5、爬楼梯(70)

该题为经典的动态规划题目,设dp[i]为爬到i级台阶总共有几种方法
1、当有1级台阶时只有一种爬楼梯的方法dp[1]=1,当有2阶台阶时有两种方法dp[2]=2,
1)爬两次,一次1阶
2)爬一次一次2阶。
当有3级台阶时则有dp[2]+dp[1],此处可以这么理解:若想爬到第三级台阶,有两种方法,爬到第一级台阶后爬2级,或爬到第二级台阶后爬1级,因此第三级台阶共有dp[3]=dp[2]+dp[1]=3种方法。
2、写出状态转移方程 dp[i] = dp[i-2]+dp[i-1]
3、给出初始条件 dp[0]=1,dp[1]=1
class Solution:
def climbStairs(self, n: int) -> int:
dp = [0]*(n+1)
dp[0], dp[1] = 1, 1
for i in range(2,n+1):
dp[i] = dp[i-1]+dp[i-2]
return dp[-1]
# 观察后发现,其实没必要存储所有的结果,只需要保存dp[i-1]和dp[i-2]即可
# 对上面的方法进行优化可写为
class Solution:
def climbStairs(self, n: int) -> int:
a, b = 1, 1 # a=dp[0],b=dp[1]
for i in range(2,n+1):
a, b = b, a+b # dp[i-1],dp[i] = dp[i-1], dp[i-1]+dp[i-2]
return b
LeetCode 热题100简单部分(一)完
知乎专栏