PTA 贪心法

  文章目录

目录

一、判断题

二、单选题

三、编程题

1.冒泡法排序

2.旅游规划

3.城市间紧急救援

4.公路村村通

5.哈利·波特的考试

6.修理牧场

7.哈夫曼编码

8.装箱问题

9.To Fill or Not to Fill

10.月饼

11.会场安排问题

12.活动选择问题

13.森森快递

---

一、判断题

1.

对N个不同的数据采用冒泡排序进行从大到小的排序，当元素基本有序时交换元素次数肯定最多。

答案：F错误

---

2.

如果 e 是有权无向图 G 唯一的一条最短边，那么边 e 一定会在该图的最小生成树上。

答案：T正确

---

3.

哈夫曼树是带权路径长度最短的树，权值较大的结点离根较近。

答案：T正确

---

二、单选题

1.

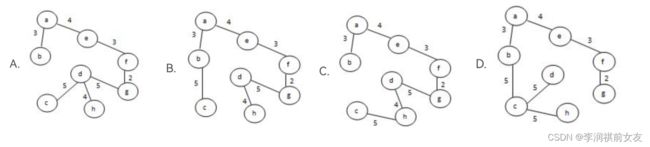
以下哪个不是给定无向带权图的最小生成树？

 答案：D

---

2.

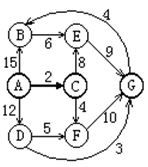
试利用 Dijkstra 算法求下图中从顶点 A 到其他顶点的最短距离及对应的路径。下列那个序列给出了可能的顶点收集顺序？

A.ACFEDBG

B.ACDBFEG

C.ACDGFBE

D.ABCDEFG

答案：A

---

3.

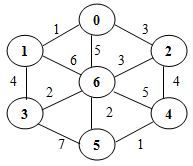
给出如下图所示的具有 7 个结点的网 G，采用Prim算法，从4号结点开始，给出该网的最小生成树。下列哪个选项给出了正确的树结点收集顺序？

A.4501362

B.4526301

C.4561023

D.4563201

答案：D

---

 4.

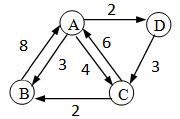
试利用Floyed算法，求下图所示有向图的各对顶点之间的最短路径。下列选项哪个给出了正确的最短路径长度矩阵和最短路径矩阵？

答案：C

---

 三、编程题

1.冒泡法排序

将N个整数按从小到大排序的冒泡排序法是这样工作的：从头到尾比较相邻两个元素，如果前面的元素大于其紧随的后面元素，则交换它们。通过一遍扫描，则最后一个元素必定是最大的元素。然后用同样的方法对前N−1个元素进行第二遍扫描。依此类推，最后只需处理两个元素，就完成了对N个数的排序。

本题要求对任意给定的K（

输入格式：

输入在第1行中给出N和K（1≤K

输出格式：

在一行中输出冒泡排序法扫描完第K遍后的中间结果数列，数字间以空格分隔，但末尾不得有多余空格。

#include
using namespace std;
const int N=110;
int a[N];
int main()
{
    int n,k;cin>>n>>k;
    for(int i=1;i<=n;i++)cin>>a[i];
    for(int i=1;i<=k;i++)
    {
        for(int j=1;j<=n-i;j++)
        {
            if(a[j]>a[j+1])
            {
                a[j]=a[j]+a[j+1];
                a[j+1]=a[j]-a[j+1];
                a[j]=a[j]-a[j+1];
            }
        }
    }
    cout<

---

2.旅游规划

有了一张自驾旅游路线图，你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序，帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的，那么需要输出最便宜的一条路径。

输入格式:

输入说明：输入数据的第1行给出4个正整数N、M、S、D，其中N（2≤N≤500）是城市的个数，顺便假设城市的编号为0~(N−1)；M是高速公路的条数；S是出发地的城市编号；D是目的地的城市编号。随后的M行中，每行给出一条高速公路的信息，分别是：城市1、城市2、高速公路长度、收费额，中间用空格分开，数字均为整数且不超过500。输入保证解的存在。

输出格式:

在一行里输出路径的长度和收费总额，数字间以空格分隔，输出结尾不能有多余空格。

#include
using namespace std;
const int N=550;
int g[N][N],p[N][N];
bool st[N];
int dis[N],pay[N];
int n,m,s,d;
void dijkstra()
{
    memset(dis,0x3f,sizeof dis);memset(pay,0x3f,sizeof pay);
    dis[s]=0;pay[s]=0;
    for(int i=0;i>n>>m>>s>>d;
    for(int i=0;i>a>>b>>x>>y;
        g[a][b]=g[b][a]=x;
        p[a][b]=p[b][a]=y;
    }
    dijkstra();
}

---

3.城市间紧急救援

作为一个城市的应急救援队伍的负责人，你有一张特殊的全国地图。在地图上显示有多个分散的城市和一些连接城市的快速道路。每个城市的救援队数量和每一条连接两个城市的快速道路长度都标在地图上。当其他城市有紧急求助电话给你的时候，你的任务是带领你的救援队尽快赶往事发地，同时，一路上召集尽可能多的救援队。

输入格式:

输入第一行给出4个正整数N、M、S、D，其中N（2≤N≤500）是城市的个数，顺便假设城市的编号为0 ~ (N−1)；M是快速道路的条数；S是出发地的城市编号；D是目的地的城市编号。

第二行给出N个正整数，其中第i个数是第i个城市的救援队的数目，数字间以空格分隔。随后的M行中，每行给出一条快速道路的信息，分别是：城市1、城市2、快速道路的长度，中间用空格分开，数字均为整数且不超过500。输入保证救援可行且最优解唯一。

输出格式:

第一行输出最短路径的条数和能够召集的最多的救援队数量。第二行输出从S到D的路径中经过的城市编号。数字间以空格分隔，输出结尾不能有多余空格。

#include
using namespace std;
const int N=550;
int n,m,s,d;
int army[N],dis[N];
int g[N][N];
bool st[N];
int path[N],pathnum[N],armynum[N],pathcity[N];
void dijkstra()
{
    memset(dis,0x3f,sizeof dis);
    dis[s]=0;pathnum[s]=1;armynum[s]=army[s];
    for(int i=0;iarmy[t])))
                t=j;
        }
        st[t]=true;
        for(int j=0;jarmynum[j])
                {
                    armynum[j]=armynum[t]+army[j];
                    path[j]=t;
                }
            }
        }   
    }
}
int main()
{
    memset(g,0x3f,sizeof g);
    cin>>n>>m>>s>>d;
    for(int i=0;i>army[i];
    for(int i=0;i>a>>b>>c;
        g[a][b]=g[b][a]=c;
    }
    dijkstra();
    cout<=0;i--)
    {
        if(i)cout<

---

4.公路村村通

现有村落间道路的统计数据表中，列出了有可能建设成标准公路的若干条道路的成本，求使每个村落都有公路连通所需要的最低成本。

输入格式:

输入数据包括城镇数目正整数N（≤1000）和候选道路数目M（≤3N）；随后的M行对应M条道路，每行给出3个正整数，分别是该条道路直接连通的两个城镇的编号以及该道路改建的预算成本。为简单起见，城镇从1到N编号。

输出格式:

输出村村通需要的最低成本。如果输入数据不足以保证畅通，则输出−1，表示需要建设更多公路。

#include
using namespace std;
const int N=1010;
int dis[N];
int g[N][N];
bool st[N];
int n,m;
int prim()
{
    memset(dis,0x3f,sizeof dis);
    int res=0;
    for(int i=0;i>n>>m;
    memset(g,0x3f,sizeof g);
    for(int i=0;i>a>>b>>c;
        g[a][b]=g[b][a]=c;
    }
    int x=prim();
    if(x==0x3f3f3f3f)
        cout<<-1<

---

5.哈利·波特的考试

哈利·波特要考试了，他需要你的帮助。这门课学的是用魔咒将一种动物变成另一种动物的本事。例如将猫变成老鼠的魔咒是haha，将老鼠变成鱼的魔咒是hehe等等。反方向变化的魔咒就是简单地将原来的魔咒倒过来念，例如ahah可以将老鼠变成猫。另外，如果想把猫变成鱼，可以通过念一个直接魔咒lalala，也可以将猫变老鼠、老鼠变鱼的魔咒连起来念：hahahehe。

现在哈利·波特的手里有一本教材，里面列出了所有的变形魔咒和能变的动物。老师允许他自己带一只动物去考场，要考察他把这只动物变成任意一只指定动物的本事。于是他来问你：带什么动物去可以让最难变的那种动物（即该动物变为哈利·波特自己带去的动物所需要的魔咒最长）需要的魔咒最短？例如：如果只有猫、鼠、鱼，则显然哈利·波特应该带鼠去，因为鼠变成另外两种动物都只需要念4个字符；而如果带猫去，则至少需要念6个字符才能把猫变成鱼；同理，带鱼去也不是最好的选择。

输入格式:

输入说明：输入第1行给出两个正整数N (≤100)和M，其中N是考试涉及的动物总数，M是用于直接变形的魔咒条数。为简单起见，我们将动物按1~N编号。随后M行，每行给出了3个正整数，分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100)，数字之间用空格分隔。

输出格式:

输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度，中间以空格分隔。如果只带1只动物是不可能完成所有变形要求的，则输出0。如果有若干只动物都可以备选，则输出编号最小的那只。

#include
using namespace std;
const int N=110;
int dis[N];
int g[N][N];
bool st[N];
int n,m;
void dijkstra(int p)
{
    memset(dis,0x3f,sizeof dis);
    memset(st,0,sizeof st);
    for(int i=1;i<=n;i++)
        dis[i]=g[p][i];
    dis[p]=0;//st[p]=true;
    for(int i=0;i>n>>m;
    for(int i=0;i>x>>y>>z;
        g[x][y]=g[y][x]=z;
    }
    int k=0,ma=1,maxx=0x3f3f3f3f;
    for(int i=1;i<=n;i++)
    {
        dijkstra(i);
        sort(dis+1,dis+n+1);
        if(dis[n]==0x3f3f3f3f)k++;
        if(dis[n]

---

6.修理牧场

农夫要修理牧场的一段栅栏，他测量了栅栏，发现需要N块木头，每块木头长度为整数Li​个长度单位，于是他购买了一条很长的、能锯成N块的木头，即该木头的长度是Li​的总和。

但是农夫自己没有锯子，请人锯木的酬金跟这段木头的长度成正比。为简单起见，不妨就设酬金等于所锯木头的长度。例如，要将长度为20的木头锯成长度为8、7和5的三段，第一次锯木头花费20，将木头锯成12和8；第二次锯木头花费12，将长度为12的木头锯成7和5，总花费为32。如果第一次将木头锯成15和5，则第二次锯木头花费15，总花费为35（大于32）。

请编写程序帮助农夫计算将木头锯成N块的最少花费。

输入格式:

输入首先给出正整数N（≤104），表示要将木头锯成N块。第二行给出N个正整数（≤50），表示每段木块的长度。

输出格式:

输出一个整数，即将木头锯成N块的最少花费。

#include
using namespace std;
int main()
{
    priority_queue,greater> q;
    int n;cin>>n;
    for(int i=0;i>c;
        q.push(c);
    }
    int res=0;
    while(q.size()>1)
    {
        int a=q.top();q.pop();
        int b=q.top();q.pop();
        res+=a+b;
        q.push(a+b);
    }
    cout<

---

7.哈夫曼编码

给定一段文字，如果我们统计出字母出现的频率，是可以根据哈夫曼算法给出一套编码，使得用此编码压缩原文可以得到最短的编码总长。然而哈夫曼编码并不是唯一的。例如对字符串"aaaxuaxz"，容易得到字母 'a'、'x'、'u'、'z' 的出现频率对应为 4、2、1、1。我们可以设计编码 {'a'=0, 'x'=10, 'u'=110, 'z'=111}，也可以用另一套 {'a'=1, 'x'=01, 'u'=001, 'z'=000}，还可以用 {'a'=0, 'x'=11, 'u'=100, 'z'=101}，三套编码都可以把原文压缩到 14 个字节。但是 {'a'=0, 'x'=01, 'u'=011, 'z'=001} 就不是哈夫曼编码，因为用这套编码压缩得到 00001011001001 后，解码的结果不唯一，"aaaxuaxz" 和 "aazuaxax" 都可以对应解码的结果。本题就请你判断任一套编码是否哈夫曼编码。

输入格式：

首先第一行给出一个正整数 N（2≤N≤63），随后第二行给出 N 个不重复的字符及其出现频率，格式如下：

c[1] f[1] c[2] f[2] ... c[N] f[N]

其中c[i]是集合{'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}中的字符；f[i]是c[i]的出现频率，为不超过 1000 的整数。再下一行给出一个正整数 M（≤1000），随后是 M 套待检的编码。每套编码占 N 行，格式为：

c[i] code[i]

其中c[i]是第i个字符；code[i]是不超过63个'0'和'1'的非空字符串。

输出格式：

对每套待检编码，如果是正确的哈夫曼编码，就在一行中输出"Yes"，否则输出"No"。

注意：最优编码并不一定通过哈夫曼算法得到。任何能压缩到最优长度的前缀编码都应被判为正确。

#include
using namespace std;
int x[100];
int main()
{
    priority_queue,greater> q;
    int WPL1=0,WPL2=0;
    int n;cin>>n;
    for(int i=1;i<=n;i++)
    {getchar();
        char c;cin>>c>>x[i];
        q.push(x[i]);
    }
    while(q.size()>1)
    {
        int c=q.top();q.pop();
        int d=q.top();q.pop();
        WPL1+=c+d;
        q.push(c+d);
    }
    int m;cin>>m;
    while(m--)
    {
        WPL2=0;
        bool flag=true;
        char str[100][100];
        for(int i=1;i<=n;i++)
        {getchar();
            char c;cin>>c>>str[i];
            WPL2+=strlen(str[i])*x[i];
        }
        if(WPL1!=WPL2)
        {flag=false;}
        else
        {
            for(int i=1;i<=n;i++)
                for(int j=1;j<=n;j++)
                    if(i!=j)
                        if(strstr(str[i],str[j])==&str[i][0])
                        {flag=false;break;}
        }
        if(flag)cout<<"Yes"<

---

8.装箱问题

假设有N项物品，大小分别为s1​、s2​、…、si​、…、sN​，其中si​为满足1≤si​≤100的整数。要把这些物品装入到容量为100的一批箱子（序号1-N）中。装箱方法是：对每项物品, 顺序扫描箱子，把该物品放入足以能够容下它的第一个箱子中。请写一个程序模拟这种装箱过程，并输出每个物品所在的箱子序号，以及放置全部物品所需的箱子数目。

输入格式：

输入第一行给出物品个数N（≤1000）；第二行给出N个正整数si​（1≤si​≤100，表示第i项物品的大小）。

输出格式：

按照输入顺序输出每个物品的大小及其所在的箱子序号，每个物品占1行，最后一行输出所需的箱子数目。

#include
using namespace std;
struct node
{
    int s,num;
}a[1010];
int b[1010],idx=1;
int main()
{
    int n;cin>>n;
    for(int i=0;i>a[i].s;
    int ma=0;
    for(int i=0;i100)
            idx++;
        a[i].num=idx,b[idx]+=a[i].s;
        ma=max(ma,idx);idx=1;
    }
    for(int i=0;i

---

9.To Fill or Not to Fill

With highways available, driving a car from Hangzhou to any other city is easy. But since the tank capacity of a car is limited, we have to find gas stations on the way from time to time. Different gas station may give different price. You are asked to carefully design the cheapest route to go.

Input Specification:

Each input file contains one test case. For each case, the first line contains 4 positive numbers: Cmax​ (≤ 100), the maximum capacity of the tank; D (≤30000), the distance between Hangzhou and the destination city; Davg​ (≤20), the average distance per unit gas that the car can run; and N (≤ 500), the total number of gas stations. Then N lines follow, each contains a pair of non-negative numbers: Pi​, the unit gas price, and Di​ (≤D), the distance between this station and Hangzhou, for i=1,⋯,N. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the cheapest price in a line, accurate up to 2 decimal places. It is assumed that the tank is empty at the beginning. If it is impossible to reach the destination, print The maximum travel distance = X where X is the maximum possible distance the car can run, accurate up to 2 decimal places.

#include
using namespace std;
const int M=3e4+10;
double pr[M];
int main()
{
    int c,d,avg,n;
    for(int i=0;i>c>>d>>avg>>n;
    for(int i=0;i>pri;
        int dis;cin>>dis;
        for(int j=dis+1;j<=dis+c*avg&&j<=M;j++)
            pr[j]=min(pr[j],pri/avg);
    }
    int now=1;
    double cost=0;
    while(now<=d)
    {
        if(pr[now]!=M)
            cost+=pr[now];
        else
            break;
        now++;
    }
    now--;
    if(now==d)printf("%.2f",cost);
    else printf("The maximum travel distance = %.2f",(double)now);
}

---

10.月饼

月饼是中国人在中秋佳节时吃的一种传统食品，不同地区有许多不同风味的月饼。现给定所有种类月饼的库存量、总售价、以及市场的最大需求量，请你计算可以获得的最大收益是多少。

注意：销售时允许取出一部分库存。样例给出的情形是这样的：假如我们有 3 种月饼，其库存量分别为 18、15、10 万吨，总售价分别为 75、72、45 亿元。如果市场的最大需求量只有 20 万吨，那么我们最大收益策略应该是卖出全部 15 万吨第 2 种月饼、以及 5 万吨第 3 种月饼，获得 72 + 45/2 = 94.5（亿元）。

输入格式：

每个输入包含一个测试用例。每个测试用例先给出一个不超过 1000 的正整数 N 表示月饼的种类数、以及不超过 500（以万吨为单位）的正整数 D 表示市场最大需求量。随后一行给出 N 个正数表示每种月饼的库存量（以万吨为单位）；最后一行给出 N 个正数表示每种月饼的总售价（以亿元为单位）。数字间以空格分隔。

输出格式：

对每组测试用例，在一行中输出最大收益，以亿元为单位并精确到小数点后 2 位。

#include
using namespace std;
const int N=1010;
struct node
{
    double w,v;
    double ave;
}a[N];
bool cmp(node x,node y)
{
    return x.ave>y.ave;
}
int main()
{
    int n,d;cin>>n>>d;
    for(int i=0;i>a[i].w;
    for(int i=0;i>a[i].v,a[i].ave=a[i].v/a[i].w;
    sort(a,a+n,cmp);
    double W=0,V=0;
    for(int i=0;i

---

11.会场安排问题

假设要在足够多的会场里安排一批活动，并希望使用尽可能少的会场。设计一个有效的
贪心算法进行安排。（这个问题实际上是著名的图着色问题。若将每一个活动作为图的一个
顶点，不相容活动间用边相连。使相邻顶点着有不同颜色的最小着色数，相应于要找的最小
会场数。）

输入格式:

第一行有 1 个正整数k，表示有 k个待安排的活动。
接下来的 k行中，每行有 2个正整数，分别表示 k个待安排的活动开始时间和结束时间。时间
以 0 点开始的分钟计。

输出格式:

输出最少会场数。

#include
using namespace std;
const int N=2e5;
int s[N],e[N];
int main()
{
    int n;cin>>n;
    for(int i=0;i>s[i]>>e[i];
    sort(s,s+n);sort(e,e+n);
    int num=0;
    for(int i=0,j=0;i=e[j])j++;
        else num++;
    }
    cout<

---

12.活动选择问题

假定一个有n个活动(activity)的集合S={a1​,a2​,....,an​}，这些活动使用同一个资源（例如同一个阶梯教室），而这个资源在某个时刻只能供一个活动使用。每个活动ai​都有一个开始时间si​和一个结束时间fi​，其中0<=si​=fj​或sj​>=fi​，则ai​和aj​是兼容的。在活动选择问题中，我们希望选出一个最大兼容活动集。

输入格式:

第一行一个整数n(n≤1000)；

接下来的n行，每行两个整数，第一个si​，第二个是fi​(0<=si​

输出格式:

输出最多能安排的活动个数。

#include
using namespace std;
const int N=2e5;
struct node
{
    int s,e;
}a[N];
bool cmp(node x,node y)
{
    return x.e>n;
    for(int i=0;i>a[i].s>>a[i].e;
    sort(a,a+n,cmp);
    int num=0,end=0;
    for(int i=0;i=end)num++,end=a[i].e;
    }
    cout<

---

13.森森快递

森森开了一家快递公司，叫森森快递。因为公司刚刚开张，所以业务路线很简单，可以认为是一条直线上的N个城市，这些城市从左到右依次从0到(N−1)编号。由于道路限制，第i号城市（i=0,⋯,N−2）与第(i+1)号城市中间往返的运输货物重量在同一时刻不能超过Ci​公斤。

公司开张后很快接到了Q张订单，其中j张订单描述了某些指定的货物要从Sj​号城市运输到Tj​号城市。这里我们简单地假设所有货物都有无限货源，森森会不定时地挑选其中一部分货物进行运输。安全起见，这些货物不会在中途卸货。

为了让公司整体效益更佳，森森想知道如何安排订单的运输，能使得运输的货物重量最大且符合道路的限制？要注意的是，发货时间有可能是任何时刻，所以我们安排订单的时候，必须保证共用同一条道路的所有货车的总重量不超载。例如我们安排1号城市到4号城市以及2号城市到4号城市两张订单的运输，则这两张订单的运输同时受2-3以及3-4两条道路的限制，因为两张订单的货物可能会同时在这些道路上运输。

输入格式：

输入在第一行给出两个正整数N和Q（2≤N≤105, 1≤Q≤105），表示总共的城市数以及订单数量。

第二行给出(N−1)个数，顺次表示相邻两城市间的道路允许的最大运货重量Ci​（i=0,⋯,N−2）。题目保证每个Ci​是不超过231的非负整数。

接下来Q行，每行给出一张订单的起始及终止运输城市编号。题目保证所有编号合法，并且不存在起点和终点重合的情况。

输出格式：

在一行中输出可运输货物的最大重量。

#include
using namespace std;
#define N 200005
int f[N];
long long Min[2*N+1],lazy[2*N+1];
void pushdown(int rt){
    if(!lazy[rt]) return ;
    lazy[rt*2]+=lazy[rt],lazy[rt*2+1]+=lazy[rt];
    Min[rt*2]-=lazy[rt],Min[rt*2+1]-=lazy[rt];
    lazy[rt]=0;
    return ;
}

void build(int l,int r,int rt){
    if(l==r) {
        Min[rt]=f[l];
        return;
    }
    int mid =(l+r)/2;
    build(l,mid,rt*2);
    build(mid+1,r,rt*2+1);
    Min[rt]=min(Min[rt*2],Min[rt*2+1]);
    return ;
}

long long qmin(int L,int R,int l,int r,int rt){
    if(L<=l&&R>=r)return Min[rt];
    pushdown(rt);
    int mid=(l+r)/2;
    long long sum=1e18;
    if(L<=mid) sum=min(sum,qmin(L,R,l,mid,rt*2));
    if(R>mid) sum=min(sum,qmin(L,R,mid+1,r,rt*2+1));
    return sum;
}


void Update(int L,int R,int c,int l,int r,int rt){
    if(L<=l&&R>=r){
        lazy[rt]+=c,Min[rt]-=c;
        return ;
    }
    int mid=(l+r)/2;
    if(L<=mid) Update(L,R,c,l,mid,rt*2);
    if(R>mid) Update(L,R,c,mid+1,r,rt*2+1);
    Min[rt]=min(Min[rt*2],Min[rt*2+1]);
    return ;
}

int main()
{
    int n,m;
    cin>>n>>m;
    for(int i=1;i>f[i];
    build(1,n-1,1);
    pairp[N];
    for(int i=0,l,r;i>l>>r;
        if(l>r) swap(l,r);
        p[i]={r,l};
    }
    sort(p,p+m);
    long long sum=0;
    for(int i=0;i

---