微带天线理论学习笔记（1）

微带天线

微带天线的概念是由Deschamps于1953年提出来的，它是在一块厚度远小于工作波长的介质基片的一面敷以金属辐射片、一面全部敷以金属薄层作接地板而成。

辐射片可以根据不同的要求设计成各种形状。微带天线具有质量轻、体积小和易于制造等优点，广泛应用于个人无线通信中。

微带天线的辐射机理

微带贴片天线理论上可以采用传输线模型来分析。

传输线模型

假设辐射贴片的长度近似为半波长，宽度为w，介质基片的厚度为h，工作波长为$\lambda$，可以将辐射贴片、介质基片和接地板视为一段长度为$\lambda /2$的低阻抗微带传输线，在传输线的两端断开形成开路。由于介质基片厚度$h\ll \lambda$，故电场沿着h方向基本没有变化。

首先最简单的情况：

假设电场沿着宽度w方向也没有变化，那么，在只考虑主模激励（TM₁₀模）的情况下，传输线的场结构如图，

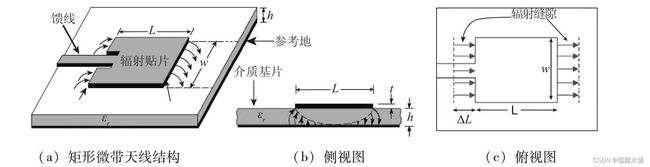
辐射基本上可以认为是由辐射贴片开路边的边缘引起的。

在两开路端的电场可以分解为相对于接地板的垂直分量和水平分量；由于辐射贴片长度约为半个波长，所以两垂直分量电场方向相反，水平分量电场方向相同。因此，两开路端的水平分量电场可以等效为在无限大平面上同相激励的两个缝隙，缝隙的宽度为$\Delta L$（近似等于基片厚度h），长度为w，两缝隙相距为半波长，缝隙的电场沿着w方向均匀分布，电场方向垂直与w

电场沿着宽度和长度方向同时变化，这时，微带天线应该用辐射贴片周围的4个缝隙的辐射来等效。

辐射场

矩形微带天线可以视为一段长L为半波长的低阻抗微带传输线，它的辐射场被认为是由传输线两端开路的缝隙所形成的。因此，矩形微带天线可以等效为长w、宽h、间距为L的二元缝隙天线阵。

单个缝隙天线的方向性函数为：

$$F(\theta ,\phi )=\frac{sin(\frac{kh}{2}sin\theta cos\phi )sin(\frac{kw}{2}cos\theta )}{\frac{kh}{2}sin\theta cos\phi \frac{kw}{2}cos\theta }sin\theta$$

h是介质板的厚度

w是介质板的宽度

k是波数

因此，矩形微带天线的辐射场只需在单缝隙天线的表达式中乘以二元阵的阵因子，所以矩形微带天线的方向性函数表示为：

$$F(\theta ,\phi )=\frac{sin(\frac{kh}{2}sin\theta cos\phi )sin(\frac{kw}{2}cos\theta )}{\frac{kh}{2}sin\theta cos\phi \frac{kw}{2}cos\theta }sin\theta cos(\frac{kL}{2}cos\phi )$$

工程上关心的是E面（$\theta =90°$）和H面（$\phi =90°$）

所以E面的方向性函数简化为：

$$F_E(\theta ,\phi )=\frac{sin(\frac{kh}{2}cos\phi )}{\frac{kh}{2}cos\phi }cos(\frac{kL}{2}cos\phi )$$

考虑$h\ll \lambda$，进一步简化

$$F_E(\theta ,\phi )=cos(\frac{kL}{2}cos\phi )$$

H面的方向性函数为

$$F(\theta ,\phi )=\frac{sin(\frac{kw}{2}cos\theta )}{\frac{kw}{2}cos\theta }sin\theta$$

输入导纳

1. 微带线馈电方式

假设馈电点到辐射贴片边缘拐角处的距离为z，则微带天线的输入导纳计算公式为：

$$Y_{in}(z)=2G[co{s}^2(\beta z)+\frac{G^2+B^2}{Y_0^2}si{n}^2(\beta z)-\frac{B}{Y_0}sin(2\beta z){]}^{-1}$$

$Y_0$是天线视作传输线的特性导纳

$\beta$是介质中的相位常数

$\beta =\frac{2\pi }{\lambda }$

G是辐射电导，B是等效电纳

$$G=\frac{I}{120{\pi }^2}$$

$$I={\int }_0^{\pi }si{n}^2(\frac{kw}{2}cos\theta )t{g}^2\theta sin\theta d\theta$$

$$B=\frac{k\Delta L\sqrt{{ϵ}_e}}{Z_0}$$

在一般情况下，$G/Y_0\ll 1,B/Y_0\ll 1$，简化为

$$Y_{in}(z)=\frac{2G}{co{s}^2(\beta z)}$$

除了$\beta z=\pi /2$外，该式均成立。可以选取不同的馈电点位置获得不同的输入阻抗。

2. 同轴线馈电方式

假设馈电点在长度L方向上离辐射贴片两端的距离分别为L1和L2，则馈电点位置的输入导纳值为

$$Y_1=Y_0[\frac{Z_{0}cos\beta L_1+j{Z}_{w}sin\beta L_1}{Z_{w}cos\beta L_1+j{Z}_{0}sin\beta L_1}+\frac{Z_{0}cos\beta L_2+j{Z}_{w}sin\beta L_2}{Z_{w}cos\beta L_2+j{Z}_{0}sin\beta L_2}]$$

$Z_0$把天线视作传输线时的特性阻抗；

$Y_w=1/Z_w$是壁导纳，其值为

$$Y_w=0.00836\frac{w}{\lambda }+j0.01668\frac{\Delta L}{h}\frac{w}{\lambda }{ϵ}_e$$

在同轴线馈线端口处，电抗可以表示为

$$X_L=\frac{377}{\sqrt{{ϵ}_r}}tg(kh)$$

输入阻抗的公式为

$$Z_{in}=\frac{1}{Y_{in}}=\frac{1}{Y_1}+j{X}_L$$

移动同轴线馈电点的位置，即改变L1和L2可使输入阻抗改变，从而获得阻抗匹配。